[codexa]統計 入門 (前編)

• 統計 入門 (前編)
• https://student.codexa.net/contents/view/44
  • 機械学習のための統計
• 対象
  • これから機械学習を学ぼうとしている人
  • 統計の基本に不安がある人

機械学習と統計

統計とは

• データを分析して、性質を調べ、推測する
  • 推測統計：採取したデータ（標本やサンプルとも呼ぶ）から母集団（全体のこと）の性質を確率統計的に推測する
  • 記述統計：収集したデータの統計量（平均、分散など）を計算して分布
    を明らかにすることにより、データの示す傾向や性質を知る

ドットプロットとヒストグラム

• バラバラとしたデータを分析しやすくグラフ化する
• 度数分布表
  • 統計資料を階級に分け、各階級ごとの度数を表の形式で表したもの。
• ドットプロット
  • 統計用グラフの一種。横軸に名義尺度（カテゴリ、番号など）を取り、1標本を1個の点（ドット）で表現する。
• ヒストグラム
  • 統計グラフの一種。縦軸に度数、横軸に階級をとって表現する。

# 使用するライブラリのインポート
import numpy as np
import matplotlib.pyplot as plt
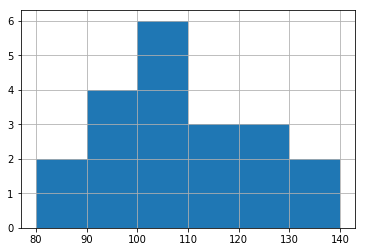
# 練習問題「ゴルフのスコア」データ作成
golf = np.array([110,107,121,137,87,92,104,129,98,99,139,82,105,100,114,122,109,94,106,111])

>
# ヒストグラムの作成
plt.hist(golf, range=[80,140], bins=6)
plt.grid(True)
plt.show()

平均値・中央値・最頻値

• 平均値（mian）
  • データの合計値をデータ数で割った値
• 中央値（median）
  • データを小さい順に並べたときにちょうど真ん中に来る値
  • データ数が偶数の場合は、２つの値の真ん中を中央値とする
• 最頻値（mode）
  • 最も頻繁に出現する値
• 四分位範囲（Interquartile range）
  • データのばらつきの大きさ（散らばり具合）を表す指標

# 使用するライブラリのインポート
import numpy as np
# 練習問題「1日のコーヒーの量」データ作成
coffee = np.array([2,2,3,5,7,9,10,15,16])
coffee.mean() #平均値(Mean)
np.median(coffee) #中央値(Median)
# 「coffee」のデータから中央値を除いて前半(Q1)と後半(Q3）に分ける
coffee_q1 = np.array([2,2,3,5])
coffee_q3 = np.array([9,10,15,16])
# Q1とQ3の中央値(Median)を求めよう
q1_median = np.median(coffee_q1)
q3_median = np.median(coffee_q3)
# IQRを算出
# 後半の中央値から前半の中央値を引く
IQR = q3_median - q1_median
# 答え確認
print(coffee_q1)
print(coffee_q3)
print(IQR)

[2 2 3 5]
[ 9 10 15 16]
10.0

分散と標準偏差

• データの散らばり具合を示すもの
• 母集団
  • 全てのデータ
• 標本
  • 母集団から一部を取り出したデータ
• 母平均 = μ（ミュー）
• 母分散
  • 平均から各データポイントがどれくらい離れているか
• 母集団標準偏差

標本標準偏差

• 標本分散
  • 標本分散は標本から計算した分散
  • 母集団に比べ標本数が少ない時は、標本分散が母分散よりも小さくなる
• 不偏分散
  • 標本分散が母分散に等しくなるように補正したもの

###　外れ値と平均値/中央値

• 外れ値 (Outlier)
  • 他の値から大きく外れた値のこと
  • 外れ値 < （Q1 - 1.5 * IQR）
  • （Q3 + 1.5 * IQR） < 外れ値