はじめに

みなさん、こんばんは。M&Aクラウドの尾村です。以前投稿した記事で、WACC（加重平均資本コスト）の算出式は天下り的に利用しました。
$$
EC = RFR + \beta(ERR - RFR)
$$
この式がなぜ用いられるのか、ベータは何者かというのを学習していこうと思います。なお、本記事の内容は概ね、財務会計・ファイナンス Rによる財務・株式データの分析を参考に書いています。
主なステップとして、以下の３段階を想定しています。

自分の言葉で理論を説明する
株価データを使って、ベータを算出し、APIから取ってきたベータと比較する
ベータを機械学習で予測してみる

CAPM（Capital Asset Pricing Model)

仮定

各投資家の最適ポートフォリオ問題を所与として（よって、各投資家が最適な戦略を知っていてそれを行なっている）、金融市場全体の均衡に関して考える。

選好：全ての投資家はポートフォリオを期待値と標準偏差の基準で評価する
取引コスト：取引に際して、コストが発生せず、ショートが可能である
流動性：証券価格は売買量に依存する
情報集合：全ての投資家は同じ情報を有する

CAPMの第一命題

「市場ポートフォリオは接点ポートフォリオと一致し、効率的フロンティア（資本市場線）上に位置する。」

市場ポートフォリオ：市場に存在する全ての危険資産を時価総額比率で保有するポートフォリオ（実用的には、TOPIX等を用いる）
接点ポートフォリオ：安全資産を保有する（危険資産の割合0）の点から、効率的フロンティアと接するように引いた直線（接線）の接点
効率的フロンティア：資産を分散投資する場合に最低限、受け入れるべきリスクの水準を表した曲線

投資家は危険資産を持つことで得られる期待収益μmから、安全資産を持つことで得られる収益（リスクフリープレミアムRF）を引いた分（μm - RF）だけ、追加の報酬が得られることを期待する。この時、資本市場線μpは、以下のように表すことができる。
$$
\mu p = RF + \frac{\mu m - RF}{\sigma m}\sigma p
$$

CAPMの第二命題

「各証券のリスクプレミアムは、その証券のマーケットベータに比例する。つまり、

$$
E[Ri] = RF + \beta i(E[RM] - RF)
$$
$$
\beta i = \frac{Cov(Ri,RM)}{Var[RM]}
$$

のように表現できる。」

ベータの分子は、市場のリターンRMとその証券のリターンRiとの共分散なので、市場との連動性を表した式になる。仮に、ベータ自体の分散が大きい場合でも、市場と負に相関している場合、適切に組み合わせることで、リスクの低減が可能になる。

マーケットベータの算出

マーケットベータの算出は、google colaboratory上で行いました。yahooqueryが使いやすそうだったので、こちらを使います。
まずは、yahooqueryをインストールしましょう。

!pip install yahooquery

エラーは適宜直してください。
次にモジュールをインポートします。今回は、yahooquery, numpy, pandas, scikit-learnを使います。


import numpy as np
import pandas as pd
from yahooquery import Ticker
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from sklearn.linear_model import LinearRegression

株価データをインポートします。今回は、私に馴染みがある「TOYO TIRE」の株価を例に算出してみました。

calc_period = '3y'
calc_interval = '1mo'
ticker = Ticker('5105.T')
df = ticker.history(period=calc_period, interval=calc_interval).reset_index()

株価は株式分割等により、変化するのでその影響を無視するため、調整後（adjclose）の値を利用します。リターン割合は（該当の月 - 前の月）　/ 該当月とします。

price = df['adjclose']
return_price = [(price[i]-price[i-1])/price[i] for i in range(1, len(price))]

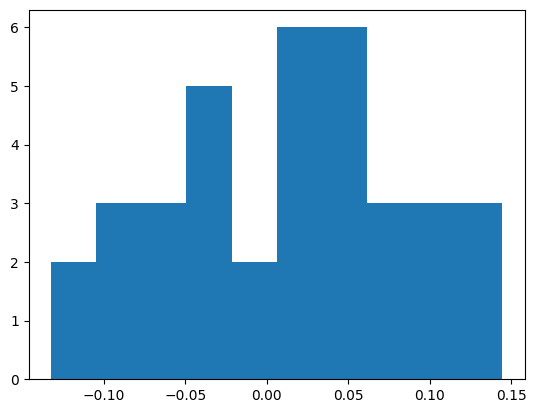
ここで、matplotlibを使って、リターンの分散を見てみます。ピークは0より大きいので一定程度のリターンは期待できそうです。

import matplotlib.pyplot as plt
plt.hist(return_price)
plt.show()

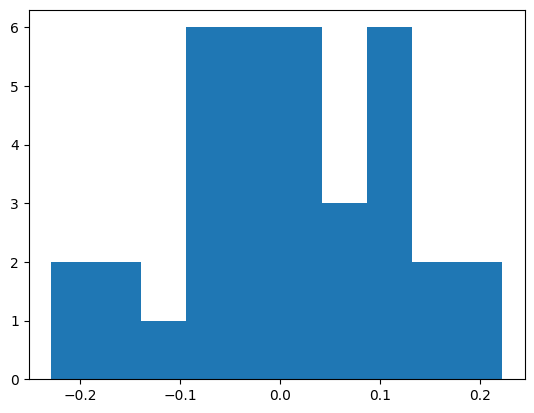
同様にTOPIXの株価も見てみます。

ticker_tpx = Ticker('TPX')
df_tpx = ticker_tpx.history(period=calc_period, interval=calc_interval).reset_index()
tpx_price = df_tpx['adjclose']
return_tpx = [(tpx_price[i] - tpx_price[i - 1])/tpx_price[i] for i in range(1, len(tpx_price))]
plt.hist(return_tpx)
plt.show()

ここから、ベータを算出するには、numpyのcov関数を使います。この関数は分散・共分散行列を算出します。２行２列の行列になり、対角成分が自己分散、非対角成分が共分散です。

cov_matrix = np.cov(return_price, return_tpx)
beta = cov_matrix[1,0] / cov_matrix[0,0]

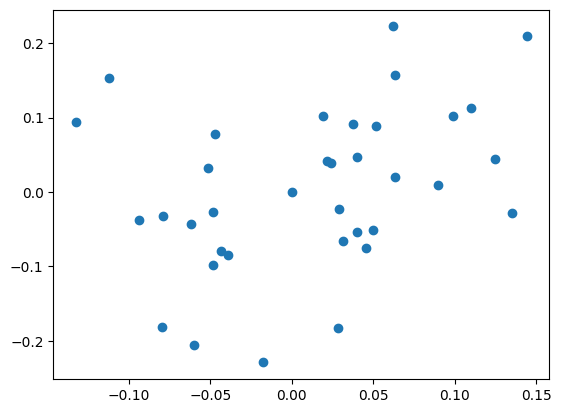
実際、どのようの分布になっているか確認するには分布図を使います。

plt.scatter(return_price, return_tpx)

かなり、分散していますが、一定程度、正の相関をしていそうです。
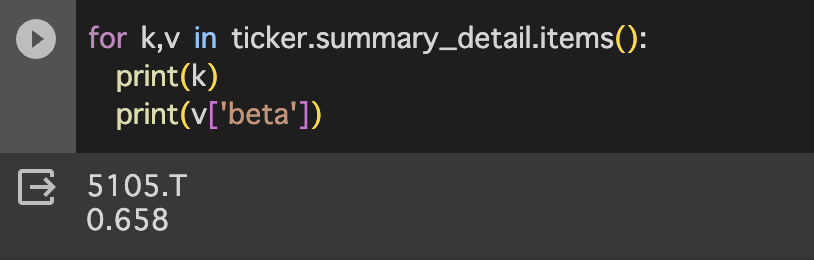
これで算出した結果が以下のようになります。

yahooqueryが算出した値は、下記のようになります。微妙に数値が違っている理由はわかりませんでした。ベータは調整のための式等も提案されているようなので、そのせいかもしれません。参考

機械学習を使って、ベータを予測する

まずは、上場企業のticker（=証券コード）の一覧が必要です。JPXのサイトから一覧をダウンロードできるので、それを使います。（pandasは、URLを指定すると、それをダウンロードして読み込んでくれるので、楽です。

listed_company_url = 'https://www.jpx.co.jp/markets/statistics-equities/misc/tvdivq0000001vg2-att/data_j.xls'
df_listed = pd.read_excel(listed_company_url, index_col=None)

yahooqueryを使って、ベータと財務諸表（BS）を収集します。

df_total = pd.DataFrame([])
for index, row in df_listed[0:1000].iterrows():
    time.sleep(0.5)
    ticker = row["コード"]
    ticker_num = str(ticker) + '.T'
    ticker_data = Ticker(ticker_num)
    if type(ticker_data.balance_sheet()) != str:
      balance_sheet = ticker_data.balance_sheet().reset_index()
      balance_sheet['ticker_name'] = row["銘柄名"]
      balance_sheet['market_product_category'] = row["市場・商品区分"]
      balance_sheet['type_33'] = row["33業種区分"]
      balance_sheet['type_17'] = row["17業種区分"]
      for k,v in ticker_data.summary_detail.items():
        if 'beta' in v.keys():
          balance_sheet['beta'] = v['beta']
        else:
          print(row["銘柄名"])
          balance_sheet['beta'] = None
      df_total = pd.concat([df_total, balance_sheet], axis = 0)

特定の条件で絞ります。

df_total = df_total.query('"2023-01-01" < asOfDate < "2023-10-31"').query("not beta.isnull()").query('currencyCode == "JPY"')

列も多すぎるとよくわからなくなるので、主観的に主要そうな項目に絞ります。

df_total = df_total[['CurrentAssets',
          'TotalNonCurrentAssets',
          'CurrentLiabilities',
          'LongTermDebtAndCapitalLeaseObligation',
          'TotalDebt', 'market_product_category',
          'type_33',
          'type_17',
          'CommonStockEquity',
          'beta']]

また、業種をonehotエンコーディングし、nanが含まれる行を削除します。drop_first=Trueがないと、今回使用する線形回帰では、多重共線性の問題にあたるので気をつけましょう。

df_total = pd.get_dummies(df_total, drop_first=True)
df_total = df_total.dropna(axis=0)

このあとはよくあるtrain/testスプリットです。

from sklearn.model_selection import train_test_split
y_cols = 'beta'
df_train, df_test = train_test_split(df_total)
X_train = df_train.drop(y_cols, axis=1)
y_train = df_train[y_cols]
X_test = df_test.drop(y_cols, axis=1)
y_test = df_test[y_cols]

BSに乗っている数値は10の何乗といった数値になるため、標準化の後、線形回帰を利用します。

scaler = StandardScaler()
X_train_std = scaler.fit_transform(X_train)
X_test_std = scaler.transform(X_test)
lr = LinearRegression()
lr.fit(X_train_std, y_train)  
y_pred = lr.predict(X_test_std)

MSEを算出すると、0.40になりました。ほとんどのベータの値が-1から1の間に収まることを考えるとこれでも、結構大きなエラーです。

予測値x軸に、正解をy軸にして、散布図を描くと以下のようになりました。少し正の相関はありそうですが、正解で負になっている数値がほとんど正に予測されているため、ここからもあまり良い結果ではなさそうです。

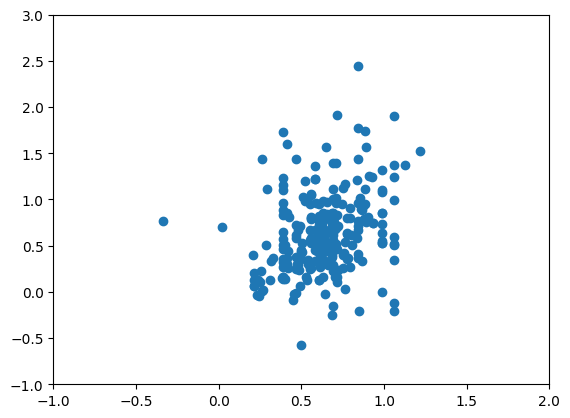
最後に各係数を求めてみると、BSの項目は一定程度、予測に寄与していそうですが、業種についてはほぼ意味がなさそうでした。

coef = lr2.coef_
df_coef = pd.DataFrame(coef).T
df_coef.columns = df_total.drop('beta',axis=1).columns
df_coef.index = ["Estimated coefficients"]
df_coef = df_coef.round(2)
df_coef

最後に

今回は、CAPMのベータの理解を深めるために、自分でベータの値を計算してみました。yahooqueryの中でベータが取得できない企業があるみたいなので、自己流の算出でも、一定程度利用用途はありそうです。また、yahooqueryからすでに求めらているベータをBSの項目を使って計算してみました。実用的に使えそうではありませんでしたが、一定、ベータの理解が深まり、（＆久々に機械学習に触れて）良かったと思います。

CAPMにおけるベータを自分で算出してみた