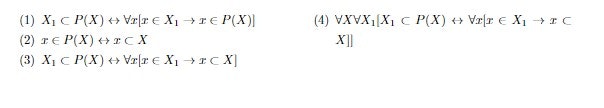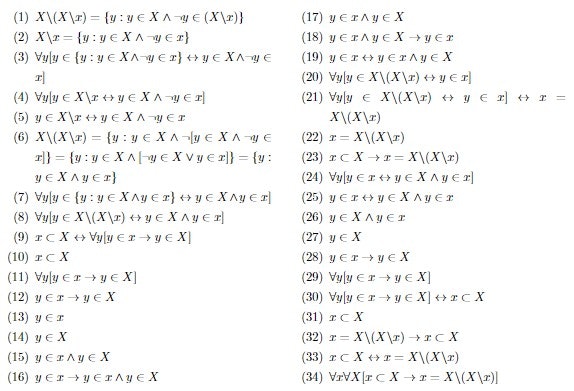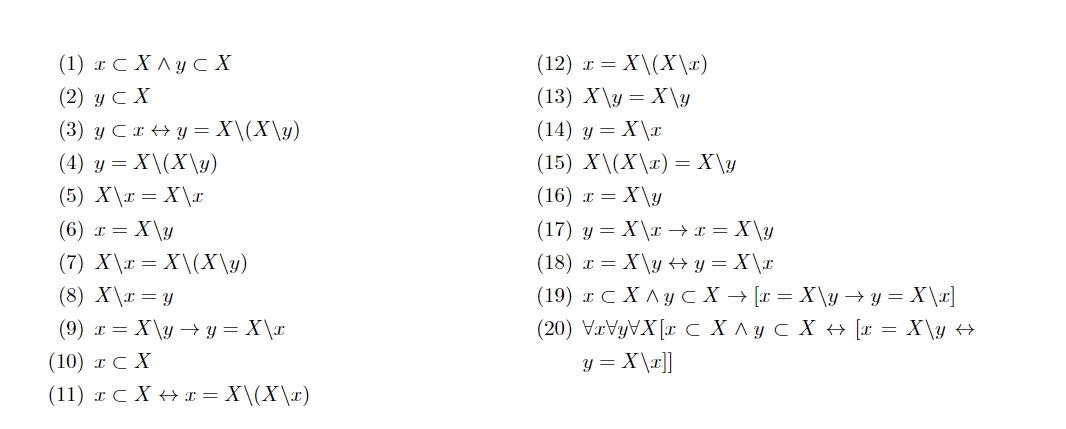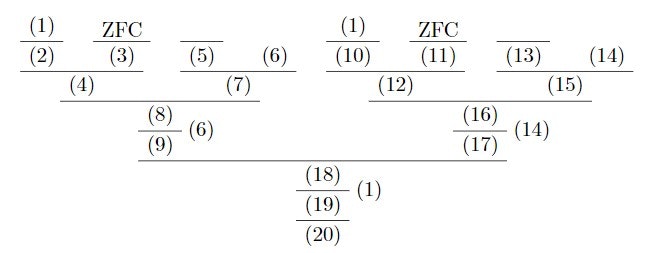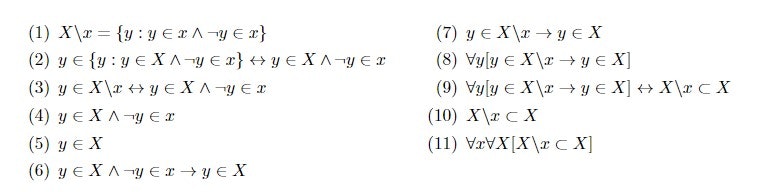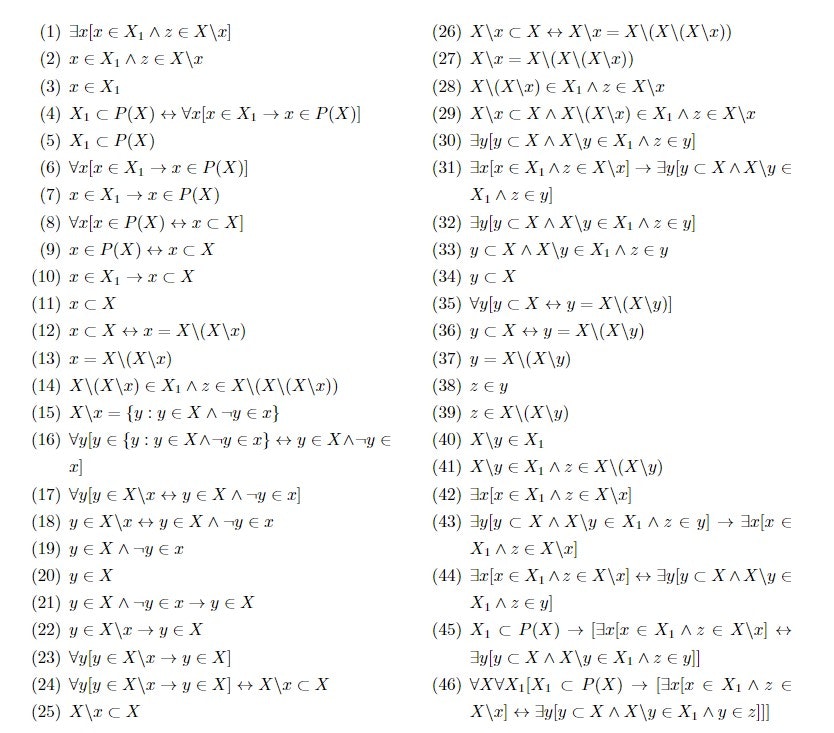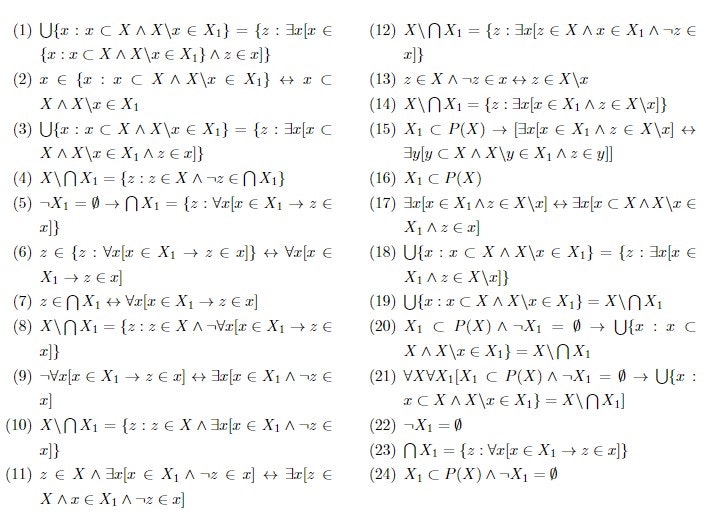あらかじめ断っておきますが、当然ながらqiitaではlatexのパッケージが自由に使えるわけではないので、今回のように大量の数式を箇条書きにしたりするのには不便です。できるのかもしれませんが、自分はやり方知りません。あと、何よりもう書く気力を失っています。てなわけで、latexで書いた数式やら証明図のスクショ貼り付けます(適当)。世界一適当な記事ですが、賛同いただける部分もあると自負しておりますので、すいません。それだけは。すいません!許してください!何でもしますから!
で、
本当は変分法の話をしたかったんだけど、そのためには位相空間やら多様体やら微分形式やらの話をしなくてはならないので、まず位相空間の話から入ろう!!!!と思ったら、いきなり閉集合の性質の証明について、どの文献も見渡す限り「明らかである」と書いて一切証明無し。それはあかんでしょ。明らかってなんじゃ???????
閉集合の性質をきちんと証明するにはまずド・モルガンの法則を証明しなくてはならない。ここではZFC公理系から自然演繹NKを用いて形式的に証明しよう。点検してないからどっか間違いあるかもしれないのでその時はコメントちょんまげ~。あ、あと、自分、数学科でも理工系でもないただの無知な馬鹿者でござりまする。そこんとこだけご理解よろしく。
さて、ZFC公理系から証明とは言ったものの、実際に仮定としてZFCに含まれるものだけを許すととてもやりにくい。例えば、ZFC公理系には補集合の表記や集合の内包的表記などが含まれていない。また、空集合の記号すら本当は必要ないらしい。集合論は定数記号や関数記号を持たないのである。確かにそれでも論理展開できるのかもしれないが(もちろん筆者はそんなことを試みたことはない)、命題の記述が非常にわかりにくいものとなってしまうだろう。
そこで、用いる表記は公理に含めてしまえば、いちいち仮定から除去する必要もなくなるし、証明の手順も減り、証明図がいくらかコンパクトになる。今回ZFC公理系と書いてい物は普通のZFC公理系に、よく使う表記方法を追加したものを意味する。
さらに、NKで証明するとは言ったものの、すべてをまじめにやっていては図がかなりでっかくなる。論理式の同値変形や命題論理の定理は何の断りもなく用いた。
以上のことにより、非常にわかりにくいかもしれないが、頑張って見ていただきたい。わたくしがやらんとしていることが何なのか感じ取っていただければと思います。同じような取り組みをしている人がいたらコメントよろしくお願いします。
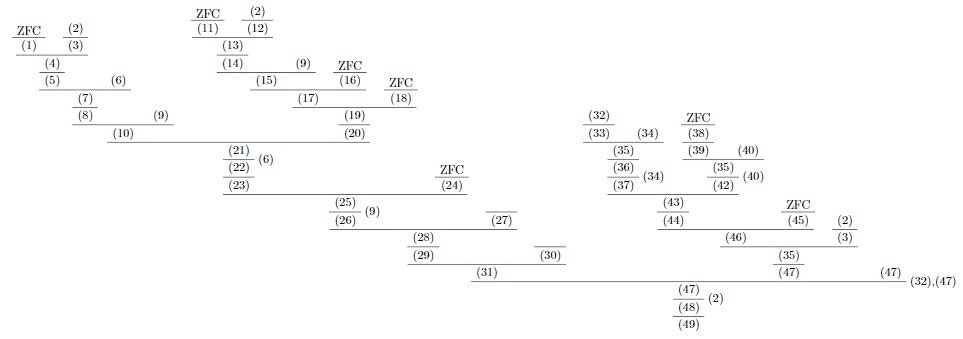
改めて、今回はド・モルガンの法則の一般化をします。
それでは以下無言になります。
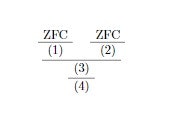
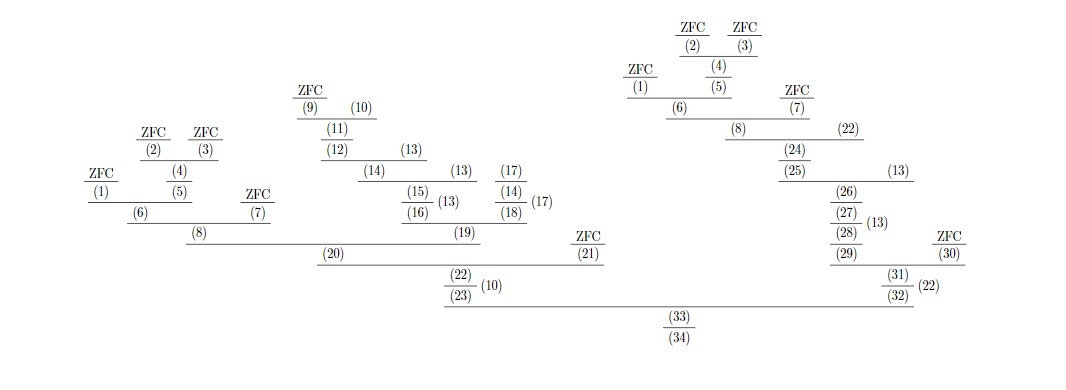
補題1
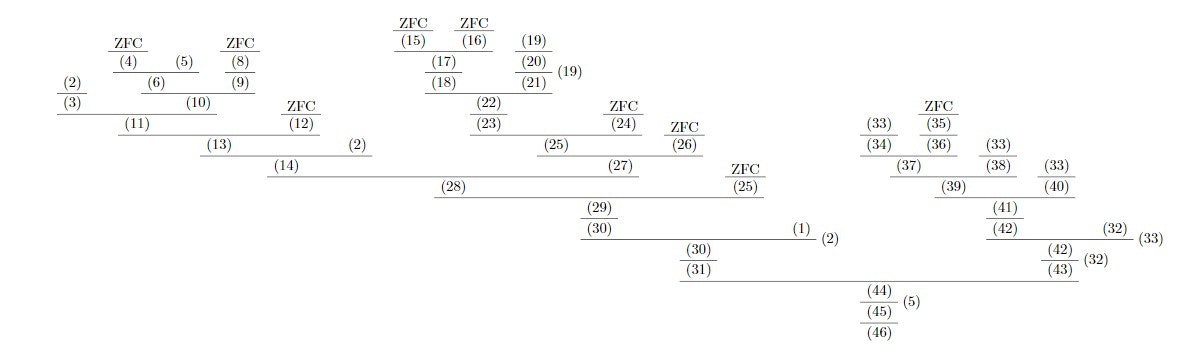
$$\text{ZFC} \vdash \forall X \forall X_1[X_1 \subset P(X) \leftrightarrow \forall x[ x \in X_1 \to x \subset X]] $$
補題2
$$\text{ZFC}\vdash \forall x [x \subset X \leftrightarrow x = X \backslash (X \backslash x)]$$
補題3
$$ZFC \vdash \forall x \forall y \forall X [ x \subset X \wedge y \subset X \leftrightarrow [ x = X \backslash y \leftrightarrow y = X \backslash x ] ]$$
補題4
$$ZFC \vdash \forall X_1 \forall X [X_1 \subset P(X)\wedge \neg X_1 = \emptyset \to \bigcap X_1 \subset X] $$
補題5
$$ZFC \vdash \forall x \forall X [X \backslash x \subset X]$$
補題6
$$\text{ZFC} \vdash \forall X \forall X_1 [X_1 \subset P(X) \to [\exists x [x \in X_1 \wedge z \in X \backslash x ]\leftrightarrow \exists y [y \subset X \wedge X \backslash y \in X_1 \wedge y \in z]]]$$
ド・モルガン1
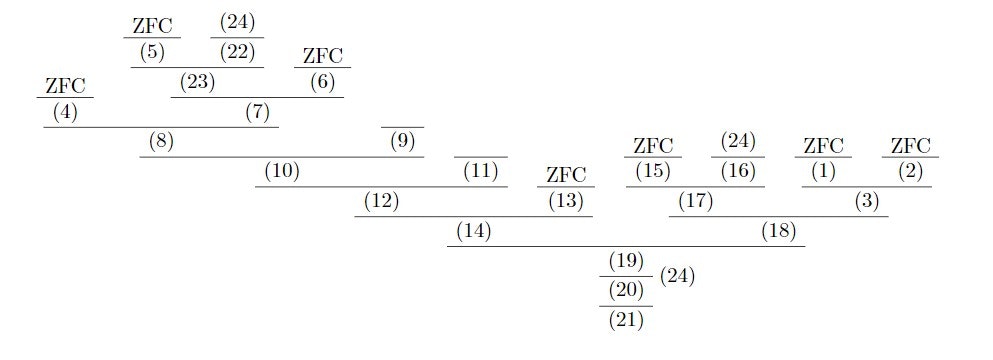
$$\text{ZFC} \vdash \forall X \forall X_1 [X_1 \subset P(X)\wedge \neg X_1 = \emptyset \to \bigcup \{ x: x \subset X \wedge X \backslash x \in X_1 \} = X \backslash \bigcap X_1] $$
ド・モルガン2
$$\text{ZFC} \vdash \forall X \forall X_1 [X_1 \subset P(x) \wedge \neg X_1 = \emptyset \to \bigcap \{ x: x \subset X \wedge X \backslash x \in X_1 \} = X \backslash \bigcup X_1]$$
戯言
今回も薄っぺらい内容な上にひどいクオリティの記事ですわな。すんまへん。
ところで、どこだったか忘れたのですが、一か所なんか変な感じの部分があるんですよ。関数記号$\bigcap$を導入しているのですが、これ実は引数に空集合を取れないんですよね。$\bigcap X = \{y: \forall x [x \in X \to y \in x] \}$このように定義されますが、$\bigcap X = \{y: \forall x [x \in \emptyset \to y \in x] \}$とすると$x \in \emptyset$が偽なので$x \in \emptyset \to y \in x$はどのような$y$に対しても真となります。自分はやってませんが、これを集合として考えるとおそらく正則性の公理と矛盾することが形式的に示されるでしょう。ですがどこかで$\forall$除去規則から$\bigcap X$を含む形の論理式を導出していました。これは、まずいですよ!関数記号の引数に制限をつけるなんてできるんですかね。よくわからないです。あと、$\{ x: \phi(x)\}$という関数記号を勝手に導入してましたが、これも怪しいです。この関数記号は項内に束縛関係を持つ関数記号となっています実際に$\phi(x)$中に自由出現する$x$を$y$に書き換えたところで、$y$が代入可能なら項の値は変わりません。つまり$\{ x: \phi(x)\} = \{ y: \phi(y)\}$ですね。でも引数に論理式を取る関数記号なんてのは一階述語論理では認められていないです。どうしようかな。。。
誰か詳しい人がいたら、数学を形式化するのに最も適している体系とか紹介してほしいです。
おしまい!
受験生諸君!今年は例年にも増してご苦労の多いことと思われますが、全ての受験生が実力を出し切り、結果にかかわらず、やり切った!という感覚を経験できることを願っております。健闘を祈る!