本記事ではAmazonレビューを元に、それが高評価か低評価か判断するタスクを取り扱います。
使うモデルはNaive BayesとBERTで今回はNaive Bayesを取り上げます。
BERTはこの記事をご覧ください。
Naive Bayesとは
今回は多項モデルではなく、ベルヌーイモデルを扱います。
ナイーブベイズはベイズの定理を応用した統計的手法です。
例としてある文章dがITというカテゴリーに含まれるかどうか考えてみることにします。
Naive Bayesではある文章dが与えられたときカテゴリITである確率を考えます。
各カテゴリに対して確率を計算し、最も確率が高いカテゴリに分類するというわけです。
これを事後確率といい次の式で表せます。
$$ P(IT|d) = \frac{P(IT)P(d|IT)}{P(d)} \propto P(IT)P(d|IT) $$
P(d) はどのカテゴリも同じなので事後確立を求めるには事前確率 P(IT) と尤度 P(d|IT) が分かればいいわけです。
P(IT) は訓練データの総文章数におけるITカテゴリの割合を調べればいいだけです。
例えば、文章が1000文あってそのうちITに関する文章が100文であれば $$ P(IT) = \frac{100}{1000} = 0.1 $$というわけです。
P(d|IT) は少し工夫が必要です。
まず前提として文章は単語の集合と考えます。
集合なので単語が文章中のどこに出てくるかは考えません(このような手法をBag-Of-Wordsといいます)。
この考えを使うと、文章dは単語wの集合として捉えることができます。
ここでもう一つ仮定をする必要があります。それは全ての単語は独立に出現するということです。
共起語を知らないのか!「機械」と「学習」はよく一緒に使われるだろうー!と怒りたくなる気持ちを抑えて次に進みましょう。
単語の出現が独立であると仮定すると、カテゴリITが与えられたときに単語wの集合である文章dが出現する確率は次にように表せます。
$$ P(d|IT) = \prod_{i = 1}^{n} P(w_i|IT) $$
P(w_i|IT) はITカテゴリ中に単語w_iが出現する確率なので、訓練データから求めれられます。
実際にはアンダーフロー対策として対数を取るのですが、ひとまずこれで確率を求めることができました。
しかし、実はまだ問題があります。
それは、未知の文章カテゴリを予測する際に、訓練データに含まれていない単語 w' を一つでも含んでいるとP(w'|IT) が0となり、P(d'|IT) も0となってしまう点です。
例えば、訓練データに使った記事がApple信者が書いたものばかりだった場合を考えてみましょう。
この場合、分類対象の文章中にiPhoneなどの単語が含まれていても、Androidが含まれてしまうとカテゴリITの確率が0になってしまいます(これをゼロ頻度問題と言います)。
これでは困るので、一定の値を与えることでこの問題が起きるのを防ぎます(この方法をスムージングと言います)。
数式で表すと次の通りです。
$$ P(w_i|IT) = \frac{Count(w_i) + \alpha}{N + \alpha V} $$
Count(x)は単語xの出現回数、NはITカテゴリの全単語数、Vは語彙数です。
こうすれば、確率が0にならないのでゼロ頻度問題を回避できます。
前処理
さて、ここからは実装をしていきましょう。
僕の実行環境は次のとおりです。
| 実行環境 | Google Colaboratory (Pro +) |
| Python | 3.8.10 |
| janome | 0.4.2 |
データは公開されているデータセットWebis Cross-Lingual Sentiment Dataset 2010を使います。
ここから入手できるものの中からcls-acl10-unprocessedを使います。
前処理済みのデータセットもあるのですが今回は勉強を兼ねて前処理からやります。
前処理のコードはこちらの本を参考にさせてもらいました。
Amazon上のレビューを直接スクレイピングすることは禁止されているので注意しましょう
まず、データセットの中身を確認します。
<item><category>本</category><raiting>4.0</raiting>
(省略)
<text>
紹介文
</text>
(省略)
</item>
前処理の仕方
- itemのタグを使って1冊ごとに分解
- 正規表現を使って紹介文とraitingを抽出
- トークナイザを使って紹介文をトークンごとに分解
これを実装します。
t = Tokenizer()
vectorizer = CountVectorizer(token_pattern='(?u)¥¥b¥¥w+¥¥b') #日本 語対応
def get_tokenized_sentences_and_labels(file_name: str):
#データの読み込み
with open(file_name) as f:
data = f.read()
data = data.replace('\n', '').replace('\r', '')
reviews = re.findall(pattern=r'<item>(.+?)</item>',string=data) #ratingはあるのにtextがない感想を取り除く
tokenized_sentences = []
labels = []
for item in reviews:
raiting = re.findall(pattern=r'<rating>(.+?)</rating>',string=item)
text = re.findall(pattern=r'<text>(.+?)</text>',string=item)
if raiting and text:
#textがある感想のみ採用
words = [token for token in t.tokenize(text[0], wakati=True)] #tokenごとに分解
a_tokenized_sentence=" ".join(words) #スペース区切りで結合
tokenized_sentences.append(a_tokenized_sentence)
raiting = int(float(raiting[0])) #5段階の評価を取得
label = 0 if raiting >= 3 else 1 #positive -> 0, negative -> 1
labels.append(label)
return tokenized_sentences, labels
def make_sample_vectors(train_file_name: str, test_file_name: str):
train_tokenized_sentences, train_y = get_tokenized_sentences_and_labels(train_file_name)
train_X = vectorizer.fit_transform(train_tokenized_sentences)
test_tokenized_sentences, test_y = get_tokenized_sentences_and_labels(test_file_name)
test_X = vectorizer.transform(test_tokenized_sentences)
return train_X, train_y, test_X, test_y
train_X, train_y, test_X, test_y = make_sample_vectors(config.input_path + 'train.review', config.input_path + 'test.review')
学習
sklearnのnaibe_bayesモジュールを用いて学習をしていきます。
Naive Bayesではスムージングの$\alpha$がハイパーパラメータとなっていますが、今回はデフォルト値のままやってみます。
興味がある方はハイパラチューニングをしてみると精度が上がるかもしれないのでやってみてください。
from sklearn.naive_bayes import BernoulliNB
cl = BernoulliNB()
cl.fit(train_X, train_y)
scoreを確認してみると0.729であることがわかりました。
混同行列は次のようになりました。
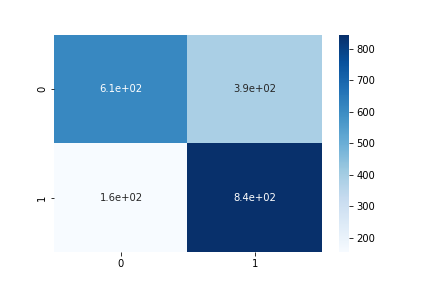
縦が実際のラベルで横が予測ラベルになっています。
ポシティブなレビューをネガティブと誤解しているケースが多いことがわかりますね。
今回実装したコードはこちらにあります。共有用に書いていたものではないので汚いです。
PATHを書き換えると動かせると思います。
パラメータを変えるなどして遊んでみてください。
まとめ
Naive Bayesは古典的な手法ではありますが、7割越えのまあまあな精度で予測することができました。
偽陰性の確率が高いことは分析する余地がありそうです。
BERT版で実験してみた記事も書いたのでこちらからぜひチェックしてください。
またこの記事は、僕が所属している 「AI・機械学習を学ぶオンラインコミュニティAcademiX」 のリレー記事です。
AIについて深く学びたい方はぜひコミュニティに参加してください!