スイングバイの基礎ー惑星探査機の軌道設計

目次

1.はじめに
2.物理量の定義
3.探査機の速度と大きさ
4.回転角
5.衝突径数Bとスイングバイ後の双曲線余剰速度
6.エネルギー変化

1. はじめに

スイングバイとは，探査機が惑星近傍を通過するときに速度が変化することを利用して，燃料消費なしに加減速を行う技術のことである．惑星中心から見ると探査機の速さは変わらないが，太陽中心から見ると惑星と探査機で運動量が交換されてお互い加減速する．本稿では，スイングバイの導出と，定性的な理解，実際のミッションで用いられた軌道の性質を考察する．

本項では，（半揚稔雄, 2014, ミッション解析と軌道設計の基礎）に沿って，省略された式を補いながら式の導出を行う．表記は統一しているが，ところどころ図に手を加えている．また、スイングバイ時にはスイングバイを行う天体の重力のみを考える近似を用いている。三体問題での月スイングバイなどは最新の研究をScholarで調べてみてください。

※誤り等ございましたら、コメントで教えていただけますと幸いです。

2. 物理量の定義

太陽を中心にする固定座標系と、スイングバイ時の惑星（中間惑星）を中心とする座標系を考える。

• $\bf{V}_P$ : 惑星の、太陽に対する公転速度
• $\bf{V}_B$ : 探査機が惑星の影響圏進入直前の、太陽に対する速度
• $\bf{V}_{\infty I}$ = $\bf{V}_B$ - $\bf{V}_P$ : 探査機が惑星の影響圏に進入する直前の、惑星に対する双曲線余剰速度（惑星に対する相対速度）
• $\bf{V}_A$ : 探査機が惑星の影響圏を脱出した直後の、太陽に対する速度
• $\bf{V}_{\infty O}$ = $\bf{V}_A$ - $\bf{V}_P$ : 惑星探査機の、影響圏脱出時の双曲線余剰速度（惑星に対する相対速度）

3. 探査機の速度と大きさ

定義より，影響圏進入時の探査機の双曲線余剰速度は，

\begin{align}
    \bf{V}_{\infty I} = \bf{V}_B - \bf{V}_P \label{1}\tag{1}
\end{align}

である。影響圏内での惑星探査機の運動について、力学的エネルギー保存則が成り立つので（惑星の公転速度が変化しないことを自明とすると）、影響圏脱出時の双曲線余剰速度の大きさ $|\bf{V}_{\infty O}|$ は進入時と等しくなる。よって，

\begin{align}
|\bf{V}_{\infty I}| = |\bf{V}_{\infty O}| = V_{\infty}
\end{align}

ここで、$V_{\infty}$ は双曲線余剰速度の大きさを表す。脱出時の速度の大きさが分かったので、あとは回転角 $\phi_B$ を求めることで、スイングバイ後の速度を求めることができる。

4. 回転角

まず，以下のように惑星中心を原点とする $\hat{\bf{R}}-\hat{\bf{S}}_I-\hat{\bf{T}}$ 直交座標を考える．

• $\hat{\bf{S_I}}$ ：探査機の双曲線余剰速度 $\bf{V}_{\infty}$ と同じ方向の単位ベクトル
• $\hat{\bf{T}}$ ：$\hat{\bf{S}}_I$ に垂直で，衝突平面内にあって，黄道面に平行な単位ベクトル
• $\hat{\bf{R}}$ ：これら２つのベクトルに垂直で，$\hat{\bf{R}} = \hat{\bf{S}}_I \times \hat{\bf{T}}$ を満たす単位ベクトル

影響圏の進入位置は，衝突平面（B-平面）内の衝突パラメータベクトル $\bf{B}$ によって定まる

• $\bf{B}$ ：惑星中心から探査機の双曲線余剰速度方向 $\bf{V}_{\infty}$ に下ろした垂線ベクトル．$\hat{\bf{T}}$ となす角を $\theta$ とする．衝突径数 $b = |\bf{B}|$ である．¹

スイングバイ軌道（双曲線軌道）の半長軸 $a$ (探査機の近心点から $\bf{V}_{\infty}$ の線の交点までの距離)は， $V{\infty} = \sqrt{{\mu}/{-a}}$ より、惑星の重力定数を $\mu = GM$として、

\begin{align}
    a = - \frac{\mu}{V_{\infty}^2} \label{2}\tag{2}
\end{align}

より，惑星の重力定数を $\mu$ として表される．さらに，近心点から中間惑星への再近接距離 $r_{\pi}$ は，惑星の(平均)半径を $R$ として，²

\begin{align}
r_{\pi} = R + h \label{3}\tag{3}
\end{align}

と表せる．

式より，関係を用いて，

\begin{align}
r_{\pi} = \dfrac{(-a)(e^2-1)}{1+e\cos{0}} = (-a)(e-1) \label{4}\tag{4}
\end{align}

これと式$(\ref{2})$より，離心率は

\begin{align}
e = 1 + \dfrac{r_{\pi}}{-a} = (-a)(e-1) \label{5}\tag{5}
\end{align}

となる．また，近心点での(惑星に対する)探査機の速度の大きさは，

\begin{align}
V_{\pi} = \sqrt{\dfrac{2\mu}{r_{\pi}}+V_{\infty}^2} \label{6}\tag{6}
\end{align}

次に，$\phi_B$ は，式 $\cos{\rho} = \frac{1}{e}$ で $\rho = \frac{\pi}{2} - \frac{\phi_B}{2}$ と置くと，

\begin{align}
\cos{\dfrac{\pi}{2}-\dfrac{\phi_B}{2}} = \dfrac{1}{e}, \quad \sin{\dfrac{\phi_B}{2}}= \dfrac{1}{e}
\end{align}

となるので，

\begin{align}
\sin{\dfrac{\phi_B}{2}} = \dfrac{1}{1+\dfrac{r_{\pi}V_{\infty}^2}{\mu}} \qquad (0^{\circ}\leq \phi_B \leq 180^{\circ}) \label{7}\tag{7}
\end{align}

と求まる．目標惑星が決まれば，回転角 $\phi_B$ は(宇宙機の速度 $||\bf{V}_B||$)と高度 $h$ のみで決まる．

====実際のミッションでは===
惑星スイングバイを用いて外惑星に行くときは、VEGA(=Venus-Earth Gravity Assist)を用いて木星などへ行くことが多い（といってもEnceladus Orbilanderなどのデカいロケットで打ち上げるミッションでは直接行くこともある）。この場合、最後の地球スイングバイでは惑星に対する探査機の相対速度が大きいため、最大回転角（スイングバイ高度が一番低い時）が小さくなってしまう。

※(半揚, 1986)より抜粋 ³

========================

5. 衝突径数Bとスイングバイ後の双曲線余剰速度

回転角 $\phi_B$ が求められると, 衝突径数 $b$は，図 9.4.6より式(7)を使って

\begin{align}
    b=(-a) e \cos \frac{\phi_B}{2}=(-a) e \sqrt{1-\sin ^2 \frac{\phi_B}{2}}=r_\pi \sqrt{1+\frac{2 \mu}{r_\pi V_{\infty}^2}} \label{8}\tag{8}
\end{align}

と得られる.

$\hat{\bf{S_I}}$ の黄経を $\lambda_I$ , 黄緯を $\beta_I$ とする。 $\hat{\bf{S_I}}$ は進入時の双曲線余剰速度 ${\bf{V_{\infty I}}}$ の単位ベクトルであるから，

\begin{align}
    \hat{\bf{S}}_I=\frac{{\bf{V}}_{\infty I}}{V_{\infty}}=\left(S_{I x}, S_{I y}, S_{I z}\right)^T=\left(\cos \beta_I \cos \lambda_I, \cos \beta_I \sin \lambda_I, \sin \beta_I\right)^T \label{9}\tag{9}
\end{align}

(3次元の極座標表示)となるので, 黄経 $\lambda_I$ は

\begin{align}
    \left.\begin{array}{l}
\cos \lambda_I=\dfrac{S_{I x}}{\sqrt{S_{I x}^2+S_{I y}^2}} \\
\sin \lambda_I=\dfrac{S_{I y}}{\sqrt{S_{I x}^2+S_{I y}^2}}
\end{array}\right\} \quad\left(0^{\circ} \leqq \lambda_I \leqq 360^{\circ}\right) \label{10}\tag{10}
\end{align}

さらに，黄緯 $\beta_I$ は

\begin{align}
\left.\begin{array}{l}
    \sin \beta_I = S_{I z}\\
    \cos{\beta_I} = \sqrt{S_{Ix}^2+S_{Iy}^2}
    \end{array}\right\}\quad\left(-90^{\circ} \leqq \beta_I \leqq 90^{\circ}\right) \label{11}\tag{11}
\end{align}

となる．${\bf{V}}_{\infty I}$ の各成分だけで全部の角度を表せた．

次に，$\hat{\bf{T}}$ と $\hat{\bf{R}}$ をそれぞれ極座標表示して，式(10, 1) を用いて ${\bf{V}}_{\infty I}$ の各成分だけで書いていく．

(黄道面に垂直で, その北極方向の単位ベクトルを $\hat{k}$ とすると), 衝突平面内で黄道面に平行な単位ベクトル $\hat{\bf{T}}$ は

\begin{align}
\notag\hat{\bf{T}}&=\frac{\hat{\bf{S}}_I \times \hat{\bf{k}}}{\left|\hat{\bf{S}}_I \times \hat{\bf{k}}\right|}=(\sin{\lambda_I}, \cos{\lambda_I}, 0)^T\\&=\left(\frac{S_{I y}}{\sqrt{S_{I x}^2+S_{I y}^2}},-\frac{S_{I x}}{\sqrt{S_{I x}^2+S_{I y}^2}}, 0\right)^T \label{12}\tag{12}
\end{align}

$\hat{\bf{T}}$ はx-y平面、つまり黄道面内に存在することに注意する。また衝突平面内で $\hat{\bf{T}}$ に垂直な単位ベクトル $\hat{\bf{R}}$ は

\begin{align}
    \notag\hat{\bf{R}}&=\hat{\bf{S}}_I \times \hat{\bf{T}}=(\sin{\beta_I}\cos{\lambda_I}, \sin{\beta_I}\sin{\lambda_I}, -\cos{\beta_I})
    \\&=
    \left(\frac{S_{I x} S_{I y}}{\sqrt{S_{I x}^2+S_{I y}^2}}, \frac{S_{I y} S_{I z}}{\sqrt{S_{I x}^2+S_{I y}^2}},-\sqrt{S_{I x}^2+S_{I y}^2}\right)^T \label{13}\tag{13}
\end{align}

となるので, 衝突パラメータ ${\bf{B}}=\left(B_x, B_y, B_z\right)^T$ は, 次の連立方程式

\begin{align*}
& {\bf{B}} \cdot \hat{\bf{S}}_I=0 \\
& {\bf{B}} \cdot \hat{\bf{T}}=b \cos \theta\\
& {\bf{B}} \cdot \hat{\bf{R}}=b \sin \theta
\end{align*}

を解くことから得られて，

\begin{align}
& B_x=\frac{b}{\sqrt{S_{I x}^2+S_{I y}^2}}\left(S_{I y} \cos \theta+S_{I x} S_{I z} \sin \theta\right) \label{14}\tag{14}\\
& B_y=\frac{b}{\sqrt{S_{I x}^2+S_{I x}^2}}\left(-S_{I x} \cos \theta+S_{I y} S_{I z} \sin \theta\right) \label{15}\tag{15} \\
& B_z=-b \sqrt{S_{I x}^2+S_{I y}^2} \sin \theta \label{16}\tag{16}
\end{align}

となる．最後に，脱出漸近線方向の双曲線余剰速度 ${\bf{V}}_{\infty O}$ は, 以下の図の幾何的関係より，

\begin{align}
    {\bf{V}}_{\infty O}={V}_{\infty}\left(\cos \phi_B \hat{\bf{S}}_I-\sin \phi_B \frac{\bf{B}}{b}\right) \label{17}\tag{17}
\end{align}

と求まる．導出過程より，太陽に対する探査機の速度 ${\bf{V_B}}$ と太陽に対する惑星の速度 ${\bf{V_P}}$ が分かれば(スイングバイの高度 $h$ をパラメータとして)スイングバイ後の速度は求まる．

6. エネルギー変化

影響圏脱出時の速度 $\bf{V_A}$ は，

\begin{align}
    \bf{V}_A = \bf{V}_P + \bf{V}_{\infty O} \label{18}\tag{18}
\end{align}

次に，探査機の運動エネルギー変化$\delta V$は，

\begin{align}
    \Delta E = \dfrac{1}{2}(\bf{V}_A^2 - \bf{V}_B^2) = \dfrac{1}{2}(\bf{V}_A+\bf{V}_B)\cdot(\bf{V}_A-\bf{V}_B) \label{19}\tag{19}
\end{align}

である．これに(18)を代入すると

\begin{align}
    \Delta E = \dfrac{1}{2}(2\bf{V}_P+\bf{V}_{\infty O}+\bf{V}_{\infty I})\cdot (\bf{V}_{\infty O}-\bf{V}_{\infty I}) = \bf{V}_{P}\cdot (\bf{V}_{\infty O}-\bf{V}_{\infty I}) \label{20}\tag{20}
\end{align}

が得られる．図より，

\begin{align}
    \bf{V}_{\infty O}-\bf{V}_{\infty I} = 2V_{\infty}\sin{\dfrac{\phi_{B}}{2}}\dfrac{\bf{V}_{\infty O}-\bf{V}_{\infty I}}{|\bf{V}_{\infty O}-\bf{V}_{\infty I}|}
\end{align} \label{21}\tag{21}

の関係が得られる．
ここで $\bf{V_P}$ と $\bf{V_{\infty O}}-\bf{V_{\infty I}}$ のなす角を $\alpha$ とすれば，

\begin{align}
    \Delta E = 2 V_P V_{\infty} \sin{\dfrac{\phi_B}{2}}\cos{\alpha} \label{22}\tag{22}
\end{align}

と書けるので，ここに代入すると，

\begin{align}
    \Delta E = \dfrac{2V_P V_{\infty}\cos{\alpha}}{1+\dfrac{r_{\pi}V_{\infty}^2}{\mu}} \label{23}\tag{23}
\end{align}

と求まる．惑星の公転速度$V_P$が大きいほど，惑星の質量が大きいほど，スイングバイ高度$h$が低いほど，$\Delta E$は大きくなることが分かる(直感と一致する)．

6.1 定性的理解

$\Delta E_{Max}$を図示すると，以下のようになる．

※(半揚, 1986)より抜粋 ³

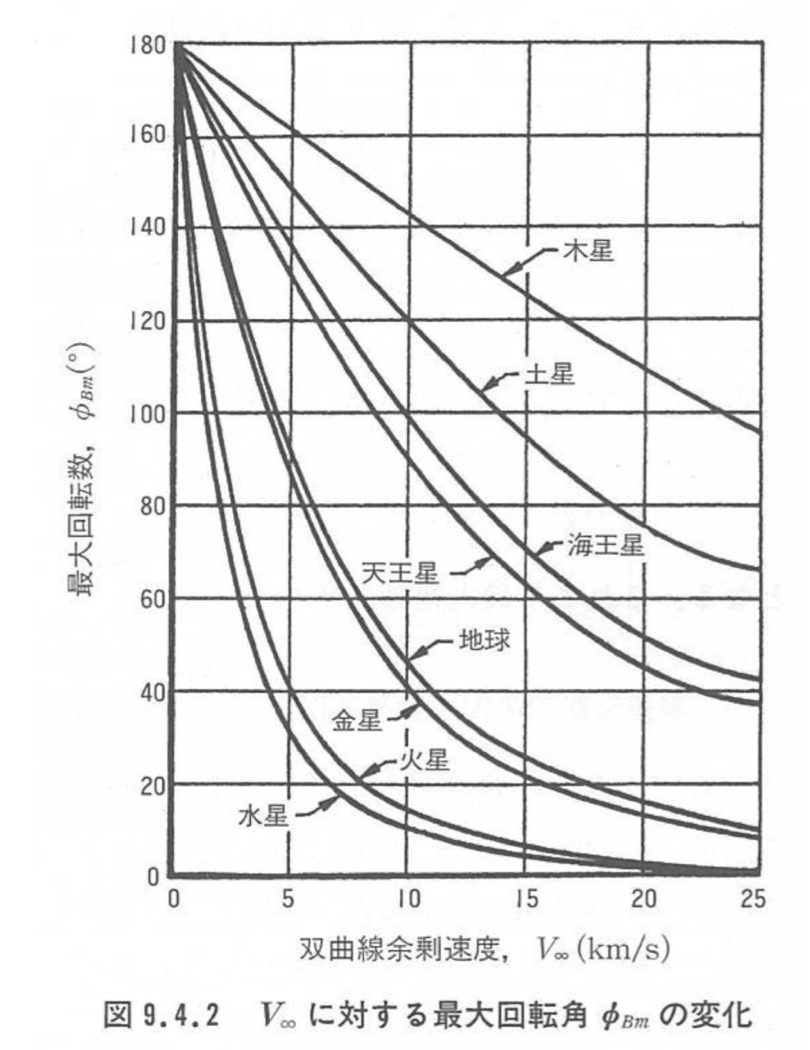
一般的に，地球から木星などの外惑星に行くときは，スイングバイによって$V_{\infty}$を段階的に大きくすることで加速を行う．このとき，地球から出発しているにも関わらず，直観に反して地球やそれより内側の金星でスイングバイを行うことが一般的である．

この理由は，図を見ることでわかる．まず，直接木星に行かない理由は地球出発に必要な$\Delta V$が非常に大きいためである．地球から出発するときの$\Delta V$が小さいと，地球や金星とスイングバイを行うときの$V_{\infty}$は小さくなる．

ここで，図より，$V_{\infty}$が小さい5 km/s あたりだと，地球や金星がエネルギーの観点で非常に効果的と分かる．これは，惑星の公転速度$V_P$が大きいからである．ここで，火星は1.5AUに存在して地球と同じくらいだが，重量が小さいので，金星や地球ほどエネルギー増加をすることができない．また，水星スイングバイを行わない理由は，金星(0.73AU)に対して水星(0.38AU)はさらに太陽に近い．わずかな差に見えるが，水星に行くには木星に行くのと同程度の$\Delta V$が必要となるのに，得られるエネルギー増分が小さいからである．

一方，地球や金星でスイングバイを行った後では$V_{\infty}$が大きくなるため，木星や土星などの公転速度$V_P$は小さいけれど質量が非常に大きい惑星が効果的となる．

以上の関係から，地球を出発した探査機が（地球）ー金星ー地球ー木星という順番にスイングバイを行うVEGA(Venus Earth Gravity Assist)がよく用いられている．派生版としてVEEGAやEVGA,火星スイングバイを経由することもある．

1. 衝突平面は扱いやすい進入余剰速度方向 $\hat{\bf{S}}_I$ を中心に組み立てられており，探査機の脱出双曲線余剰速度を扱いやすくしている． ↩

2. 探査機のミッション設計では、初期段階（最適化前の初期軌道など）ではスイングバイ時の惑星を質点として考え、使う軌道が固まってきたら重力の偏りを考慮した軌道計算を行う。 ↩

3. 半揚稔雄ほか. 中間インパルスと推力スウィングバイを含む最適惑星間軌道による飛行計画: 特に木
   星を対象として. 宇宙科学研究所報告, Vol. 44, pp. 1–102, 1986. ↩ ↩²