f-divergence一族の可視化

f-GANを読んでたら，f-divergenceというものが．

定義

$D_{f}(P\parallel Q)\equiv \int _{{\Omega }}f\left({\frac {dP}{dQ}}\right),dQ.$

二つの確率分布を比べる
fが特殊な時に名前が付いている．代表的なのは下の表にある

KL divergenceとかJS divergenceだけじゃないのかーと思い，まとめ

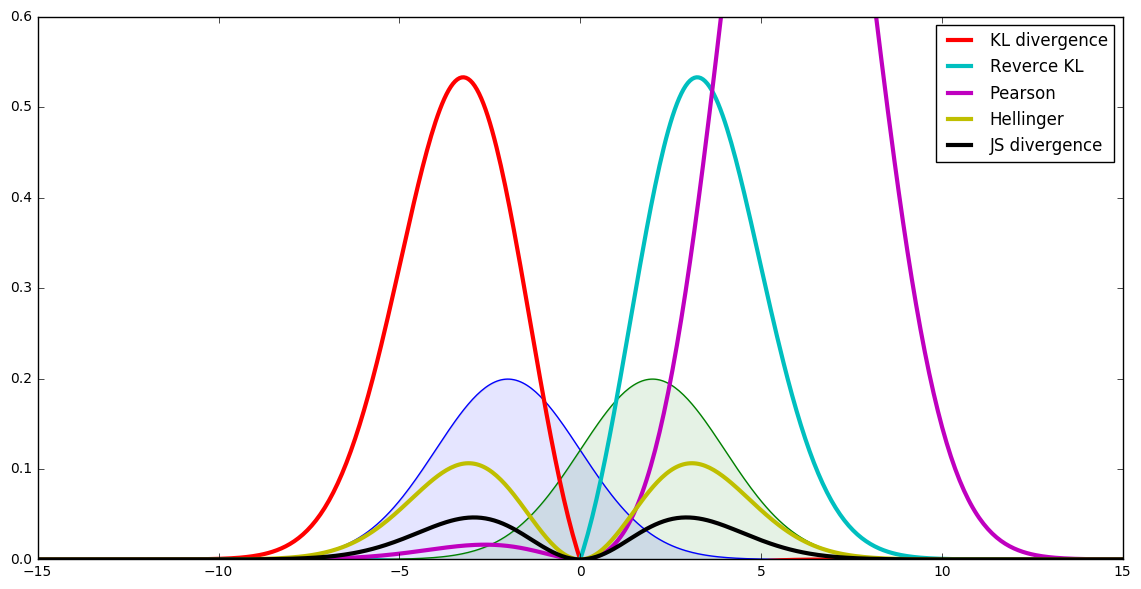
積分内の値の動き

• 例えばkLなら，$f(x) = p(x)\log{\frac{p(x)}{q(x)}}$をプロット
• $p$と$q$は正規分布$N$(網掛け青と緑)
  • $N(x,\mu,\sigma) = \frac{1}{\sqrt{2\pi\sigma^2}}\exp{\frac{-(x-\mu)^2}{\sigma^2}}$
  • $ p(x) = N(x,-2,2)$
  • $q(x) = N(x,2,2)$

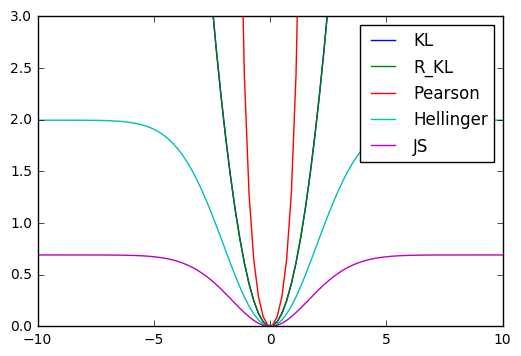
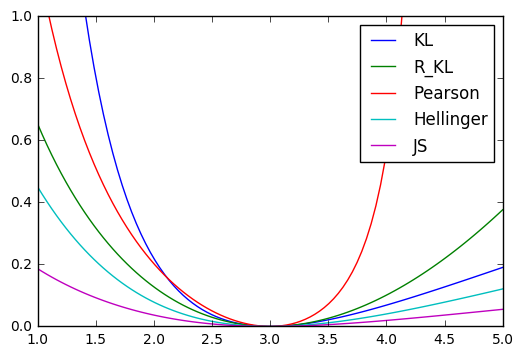
各f-divergenceの可視化はこんな感じ

• 対称非対称
• 極値の違い

などが見て取れる．f-divergenceはこの積分値

分布の変化とdivergenceの関係

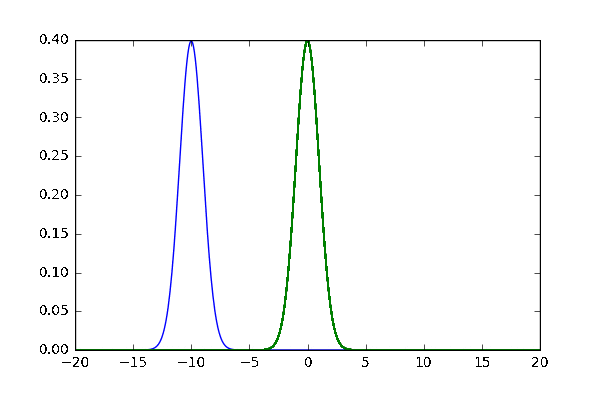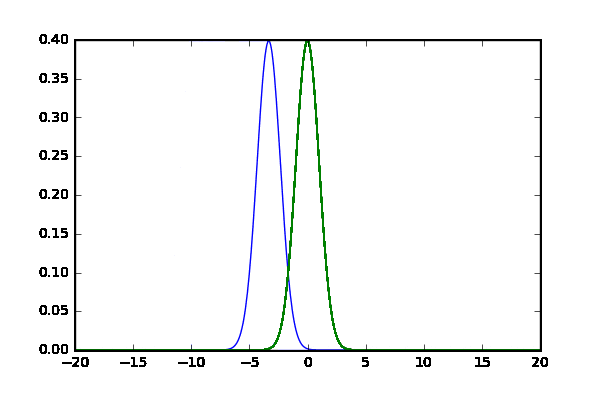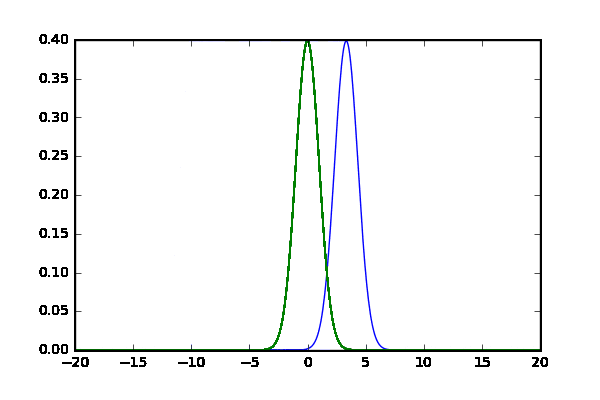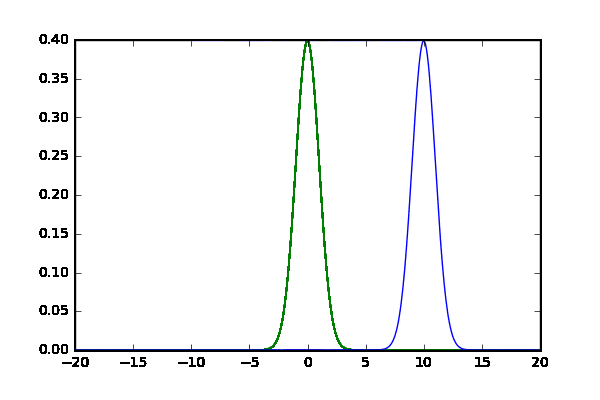
比べるものその1 平均のズレ

• $N(\mu=0,\sigma=1)$と$N(\mu_1,\sigma=1)$で，$\mu_1$を[-10,10]で動かす

gif

結果

立ち上がり方がものによって違うという感じ

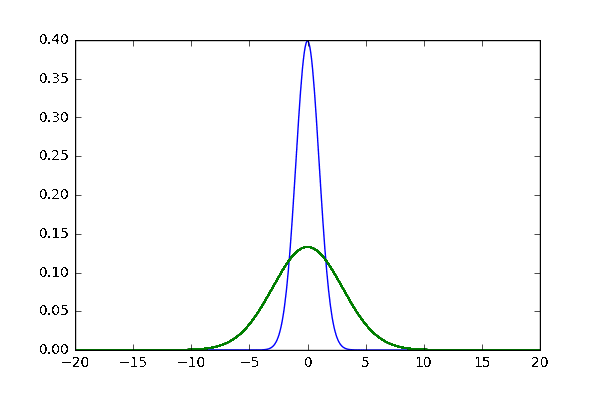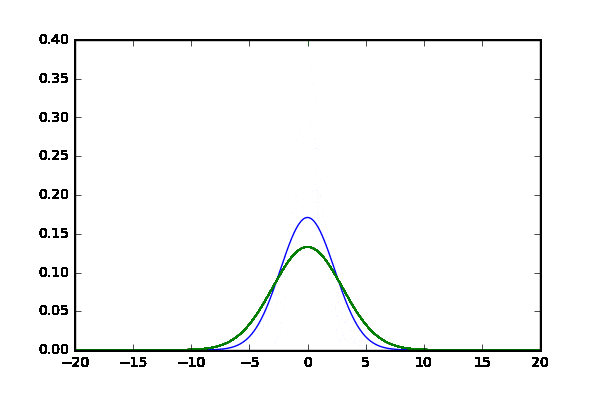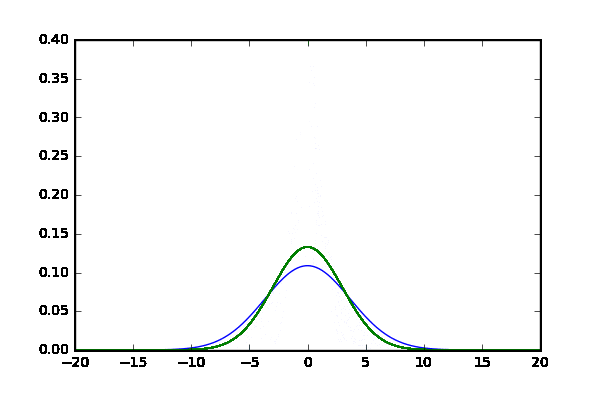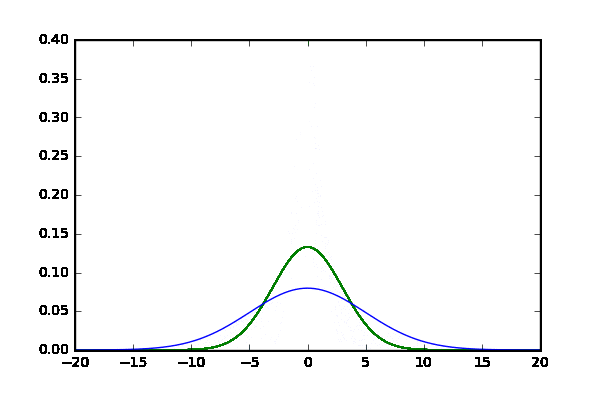
比べるものその2 分散のズレ

• $N(\mu=0,\sigma=3)$と$N(\mu_1=3,\sigma_1)$で，$\sigma_1$を[1,5]で動かす

gif

結果

反応がわりと違って面白い

その他の計量

• Histgram Intersection
• L1,L2 norm

とかをはてなブログにまとめている．そちらも参考に