再びシンギュラリティは近い
はまです.ラブライバーを拗らせた結果,推しごとがお仕事になりました.2020年7月よりKLabに勤務しています.KLabでは,最適化や機械学習でゲームの開発や運用を支援したり,前職から引き続き理研AIPで共同研究したり,進化計算学会で最適化コンペを開催したりしています.
みなさん,2017年のFUJITSU Advent Calendarにこんな記事を書いたのを覚えていますか?
シンギュラリティは近い ~全人類がいますぐ注目すべき特異点論と多目的最適化の知られざる関係~
三行でまとめるとこんな話でした:
- よくある条件下で,多目的最適化問題の解であるパレート集合は特異点集合のサブセットになる.
- パレート集合の大域的構造は,各パレート解がどんなタイプの特異点かによって決まっているかも.
- これを解明するには,大域解析を応用したSmaleの最適化理論を発展させる必要がありそう.
あれから3年,この方針にしたがって特異点論と多目的最適化の関係を研究してきました.その結果,重要な問題クラスとして知られる強凸最適化において,実際にパレート集合のトポロジーが特異点のタイプによって決まっていることがわかりました.また,強凸とは限らない状況においても近似パレート解のデータからパレート集合のトポロジーを推定することができるようになりました.ポアンカレ予想の応用です.この推定法は機械学習のハイパーパラメータ調整などにも役立つようです.これをゲーム開発に応用すれば,実際に数学で推しを推すことができそうです.人生ですね.今回はこれらの進展をお伝えしたいと思います.内容は2020年9月16日の第13回OPTA:最適化とその応用での講演に基づきます.講演スライドはSlideShareにアップしました.

当日は口頭でいろいろと補足しながら発表したので,スライドだけではわかりにくいかもしれません.そこで本記事では当日話したようなことを文章で補足していこうと思います.
目次
内容はこんな感じです.ここには書いてないのですが,最後にデータからパレート集合のトポロジーを推定する方法も話しました.
背景と目的
最初に多目的最適化とはどんな分野なのか説明し,多目的最適化におけるトポロジー研究の歴史を紹介します.
多目的最適化とその解集合
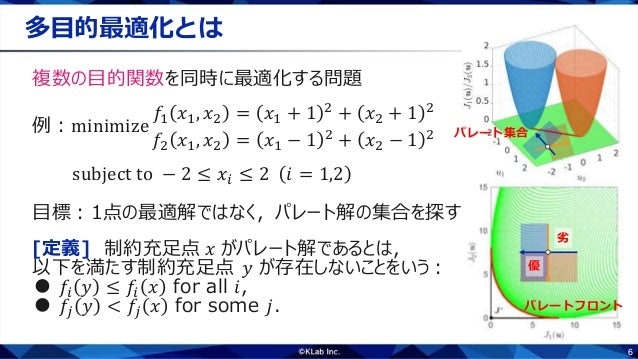
複数の目的関数を同時に最適化する問題を多目的最適化といいます.たとえば,2つの2変数関数$f_1,f_2:[-2,2]^2 \to \mathbb R$を最小化することを考えます.$f_1$の最小点は$(x_1,x_2)=(-1,-1)$で,$f_2$の最小点は$(x_1,x_2)=(1,1)$ですね.2つの関数がともに最小値をとる点はないので,2つの関数のトレードオフを考える必要があります.スライド左下の定義を見てください.もしどの関数値も大きくすることなくいずれかの関数値を小さくできるなら,そのほうが優れているといえるでしょう.しかし,もしある関数値を小さくするために他の関数値を少しでも大きくしてしまうなら優劣はつかないものとします.これがパレート順序です.パレート順序の意味でこれ以上改善できない点をパレート解といいます.パレート解の集合をパレート集合といい,パレート集合の像をパレートフロントといいます.多目的最適化の目標は,パレート集合やパレートフロントを求めることです.

様々な産業で多目的最適化が使われています.応用先としてはメーカーや重工業系,航空宇宙系が多い印象です.たとえば航空機の設計では,最適化すべき性能指標は揚力,空気抵抗,騒音,安全性,環境排出物などいくつもあります.これらは異なる物理量なので,安易に加重和をとって単目的最適化にすることもできません.製品設計に求められるすべての要素を問題の定式化に組み込むことはできないため,「ソルバの出した解がそのまま製品に使われることはない.設計者が考えるための参考値にすぎない」とよく言われます.そのため,最適解を1つだけ求めてくれるよりも,多数の解で性能指標のトレードオフ関係を明らかにしてくれることが望まれます.そういった事情から多目的最適化が好まれるのだと思います.スライドに記載した商用ソルバのリンクから応用事例集を眺めてみると,どんな分野でどんな使われ方をしているかより詳しくわかると思います.
このスライドに限らず,オレンジ色の文字はすべて出典へのリンクです.画像をクリックするとSlideShareの該当ページが開きます.SlideShareのスライド内のリンクをクリックすれば,出典のURLに飛べます.
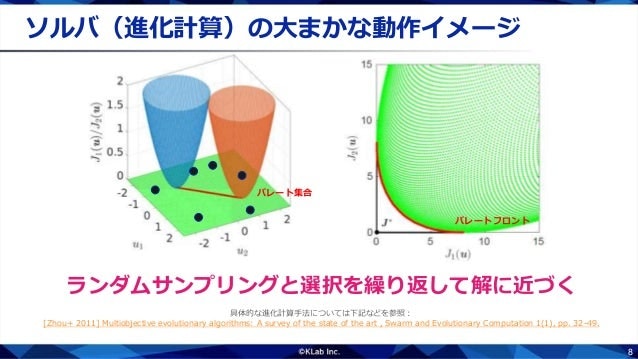
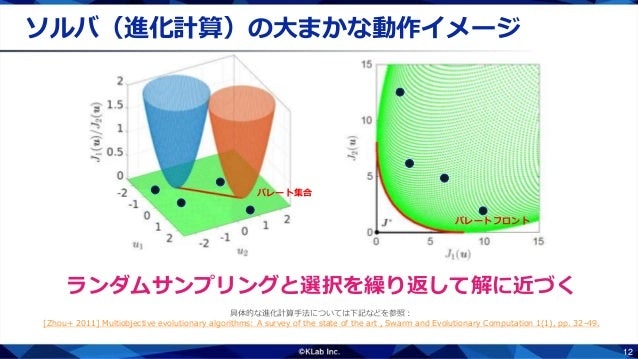
これらの商用ソルバの中身は,ほとんどが進化計算というアルゴリズムです.製品設計などでは,解の評価にシミュレータを使いることが多く,関数の凸性や微分などを利用した手法が使いにくいためです.進化計算には数え切れないほどのバリエーションがあるのですが,基本的な動作イメージは「複数点のランダムサンプリングと選択を繰り返して解に近づく」というものです.探索の流れをみてみましょう.まずは適当に点をばらまきます.
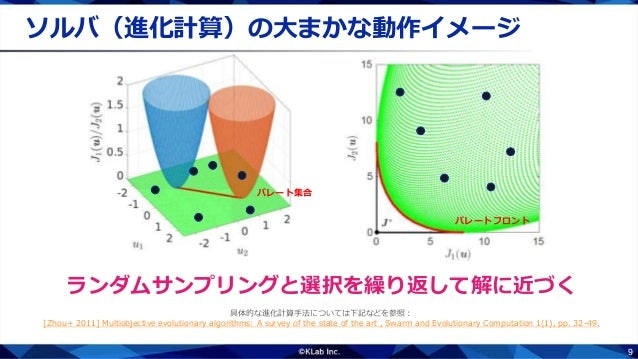
これらの点の目的関数値を計算します.各点の関数値は右図のようになったとします.
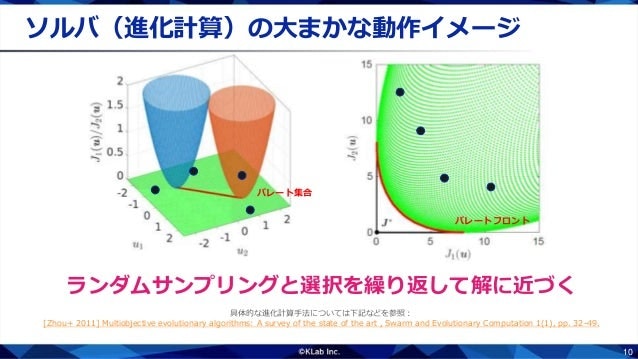
パレート順序に基づいて,劣っている点を取り除きます.すると,パレート集合に近い点たちが残ります.
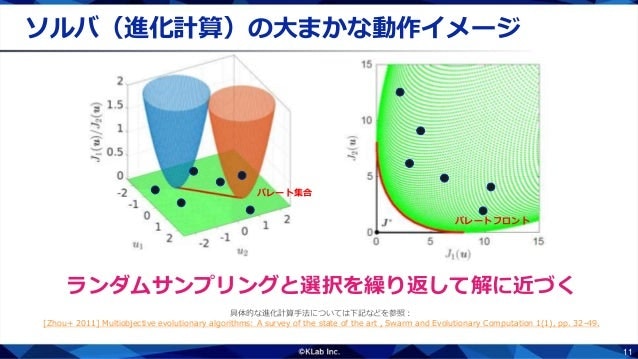
残った点の周りに新しい点をばらまきます.新しい点の目的関数値を計算し,右図のようになったとします.
再びパレート順序に基づいて,劣っている点を取り除きます.さらにパレート集合に近づきました.
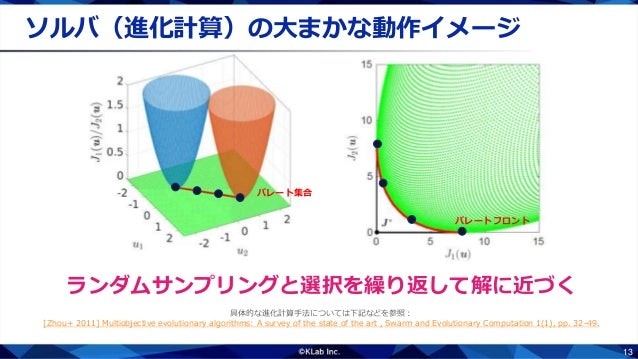
これを繰り返すとパレート集合に収束していきます.いや,実際には収束する保証はないのですが.きっと進化計算の研究者たちはこんなふうに動いてくれたらいいな~と思ってアルゴリズムを設計していると思います.
進化計算という分野ではありますが,生物のアナロジーで最適化問題のソルバを設計することに魅力を感じる人もいれば,アナロジーには興味なくてとにかく効率の良いソルバが作れればそれでヨシという人もいます.そのへんのスタンスは色々です.実際には数理計画法と進化計算の合わせ技もよく使われるので,アプローチで分野を分けることにはあまり意味がないのかもしれません.

問題が解ければ終わりかというと,そうではありません.多くの問題でパレート集合やパレートフロントは目的数-1次元になることが知られています.4目的以上ではパレート集合やパレートフロントを求めることができたとしても,図示できません.するとせっかく問題が解けてもトレードオフを理解することができなくなります.
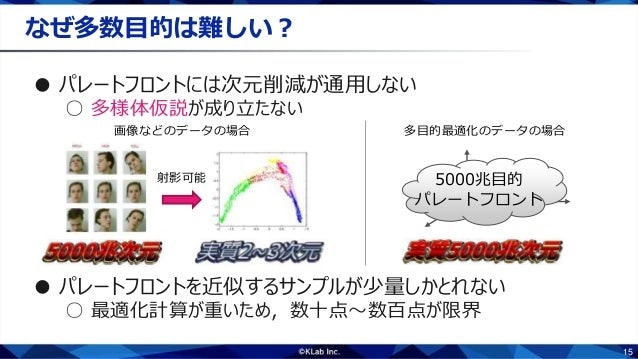
高次元のデータを理解する方法としては,次元削減などのテクニックもありますが,パレート集合やパレートフロントに対してはあまりうまくいきません.これらは内在的次元が高いので,射影すると潰れて本来の情報を失ってしまいます.さらに,最適化計算は重いため,数十点から数百点しか近似解が得られません.

高次元の対象を少数の点でどうやって理解すればいいのでしょうか.普通に考えると無理なので,多様体仮説に代わる新しい仮説を考える必要があります.そのために,パレート集合やパレートフロントがしばしばどんな構造をもっているか調べてみました.

最適化の理論ときいて真っ先に思いつくのは,凸最適化だと思います.対象を凸関数に限ることによって,超平面分離定理から生じる双対性を駆使して豊かな理論が展開できます.勾配法の理論としては適している気がしますが,大域的最適化をめざす進化計算の理論としては扱える問題クラスが狭い気もします.
一方,広い問題クラスで成り立つ理論といえば,ノーフリーランチ定理があります.どんなアルゴリズムも,すべての問題に対する平均的な探索性能は等しいと主張する定理です.これをもって「汎用ソルバは作れないんだから進化計算なんか研究しても無駄だ」という人もいます.しかしすべての問題なんか解けなくてもいいんじゃないでしょうか?現実に登場しうる多くの問題がそこそこ効率的に解ければ十分です.一方で,この定理を根拠として「進化計算はオペレータを自由に設計できるんだから,できるだけ個々の問題に特化した作り込みをすべきだ」という人もいます.しかし問題ごとに別々のソルバを使わないといけないならば,いくら性能が良くても使いにくい気がします.いずれにせよ,ノーフリーランチ定理の想定は極端すぎて,そこから現実的なアルゴリズムの設計指針を導き出せるものではないと思うわけです.
さて,大域最適化のための理論はないのだろうかと思ってググってみたら,そのまんまな名前がありました.結構昔からあるみたいですね.しかもこのSmaleという人は「数学界のノーベル賞」ともいわれるフィールズ賞を受賞したすごい数学者ですよ.

もともと多目的最適化の研究は経済学で始まったのですが,経済学における多目的最適化問題に大域解析を応用することで「目的関数の凸性を仮定することなくパレート集合の性質を解析する」なんてことをやっています.これはドンピシャな理論が見つかりました.

経済学におけるSmaleの6編のシリーズ論文を追っていくと,こんなことが(証明なしに)書いてあります.
目的関数$u:W\to \mathbb R^m$がランク仮定,ジェット横断性,横断性条件$A_1$を満たすとき,パレート臨界集合(パレート集合のスーパーセット)は滑層分割集合になる.しかも,これら3つの仮定は,写像空間においてジェネリックな性質である.
ごく一部の例外を除いてほとんどすべての問題で成り立つ性質のことを,ジェネリックな性質といいます(正確な定義はスライド内のリンクを参照してください).ジェネリックな性質に基づけば,凸関数よりもはるかに広い問題を扱うことができ,ノーフリーランチ定理とも矛盾しません.たとえば,パレート集合が滑層分割集合であるという性質は(凸性などを仮定しない)ほとんどすべての可微分写像で成り立ちます.この仮定に基づいてソルバを設計すれば,一般性をほとんど損なうことなく,探索を効率化できると期待できます.進化計算研究者が夢見た汎用ソルバを作れるかもしれません.
多目的最適化におけるトポロジー研究の歴史

しかし大域解析に基づくSmaleの最適化理論は,最適化の研究者にはあまり知られていないと思います.少なくとも大学の最適化の授業で取り上げられることはないはずです.なぜ知られていないのかはわかりませんが,私見ではその歴史に理由がある気がしています.実は,これもあまり知られていないのですが,多目的最適化におけるトポロジーの研究には半世紀以上の歴史があります.それぞれの年代の大きなトピックを紹介します.

私の知る最初の例としては,1950年代にKoopmansがアクティビティ分析の問題に多目的線形計画法を応用してノーベル経済学賞を受賞しました.その論文の中で,パレート集合(こちらの分野ではefficient setとよばれている)の可縮性を議論しています.ただしこの論文では証明はスケッチのみで,その後厳密に証明されたのかどうかわかりません.

その後も色々ありますがしばらく飛ばします.1973~1976年にかけて,Smaleが経済学を研究していました.Smaleは1960年代に高次元ポアンカレ予想を解決してフィールズ賞を受賞したのですが,そこで駆使したMorse理論をベクトル値に拡張して,大域解析に基づく多目的最適化の理論を作ろうとしました."Global Analysis and Economics"という6本のシリーズ論文を書いたのですが,その最初の論文の中で「純粋交換経済のパレート集合は単体と同相になる」と書いています.ただ,この論文には証明は書かれていないし,私の知る限りその後もずっと証明されていないみたいなのです.とはいえ,後述する観察でわかってきたことですが,「パレート集合が単体と同相」という性質は様々な多目的最適化問題でみられる基本的な性質のようなのです.

その後,多目的最適化におけるトポロジーの研究はオペレーションズリサーチに波及していきます.1970年代後半から1980年代にかけて,経済学の特定の問題からは切り離され,線形最適化問題や凸最適化問題,準凸最適化問題といった一般的な問題クラスにおいて,パレート集合やパレートフロントの閉集合性,連結性,可縮性などが議論されました.ただ,Smaleの言っていた「単体と同相」という結果は出てきません.このあたりの成果は最適化の教科書に載っていることは稀なのですが,Lucの"Theory of Vector Optimization"はそのために1章を割いた数少ない本です.

こうして多目的最適化におけるトポロジーの研究が広まるかと思いきや,1990年代には下火になります.凸解析に基づくKoopmans流のアプローチでは,凸最適化までしか扱えませんでした.そこではあまり変わったトポロジーが現れず,直観的に予想される通りの結果が示されるだけでした.そのため,早々にやることがなくなったと思われてしまったのかもしれません.
一方で,大域解析に基づくSmale流のアプローチは,非凸最適化も扱える可能性を秘めていましたが,あまり流行りませんでした.当時の非力な計算機では,凸最適化問題のパレート解を一つ求めるだけでも大変なことで,それより複雑な非凸最適化問題のパレート集合の大域的な性質がわかったところで実用性に乏しかったのではないかと思います.
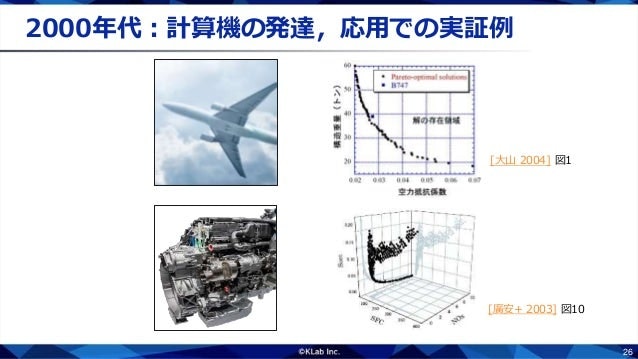
ところが2000年代に入って,計算機が速くなり,多目的最適化のための進化計算も登場しました.非凸最適化問題のパレート集合を網羅的に探索することが現実的になりました.すると,Smaleの言っていたような単体と同相なパレート集合が多くの問題で現れることがわかってきました.ただ,これらの実験結果を出している最近の研究者には,Smaleの仕事はほとんど知られていません.そのため理論と実践が相変わらずバラバラになっているというのが現状です.

2014年になって,オペレーションズリサーチにおいても,一般的な問題クラスにおいて「単体と同相」に言及する研究者が現れました.ただし厳密ではなく,少し考えれば反例が見つかったりします.Lovisonは商用ソルバmodeFRONTIERの開発元ESTECO Research Lab.に勤めていた数学者で,Smaleの経済学論文を引用するなど,Smaleの多目的最適化理論を意識した研究を行っています.

さて,ここまでが研究の背景です.背景だけでもあまり知られていない話ばかりで長くなったので,ここでいったんまとめます.産業界としては,2000年頃より多目的最適化の応用がさかんになっていました.しかし,4目的以上の最適化では,解の構造が理解困難で応用が進んでいませんでした.一方,学術界としては,多目的最適化のトポロジーは半世紀前から研究されてきました.大きく分けて凸解析と大域解析という2つのアプローチがありましたが,いずれも理論中心で産業応用には至っていませんでした.
単体的な問題

ここからが私の研究の話になります.1つめは,Smaleの言い出した「単体と同相」をきちんと定式化してみた,という話です.
実問題の解集合の傾向

「単体と同相」な問題がどれくらいあるのか,実問題を調べてみました.進化計算分野のトップ会議GECCOの最近5年の論文を網羅的に調べて,そこで扱われている実問題のパレートフロントを観察しました.一部をピックアップして紹介します.
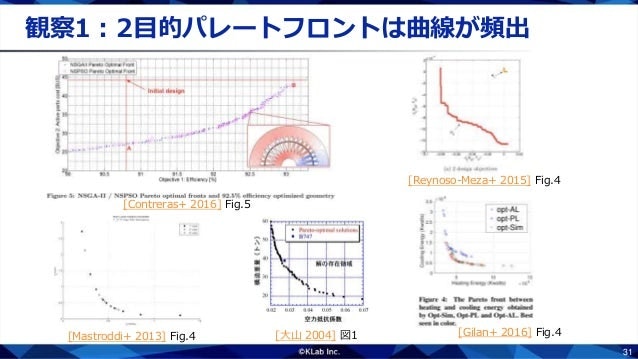
2目的最適化問題のパレートフロントは曲線になることが多いようです.

3目的最適化問題のパレートフロントは曲がった三角形になることが多いようです.
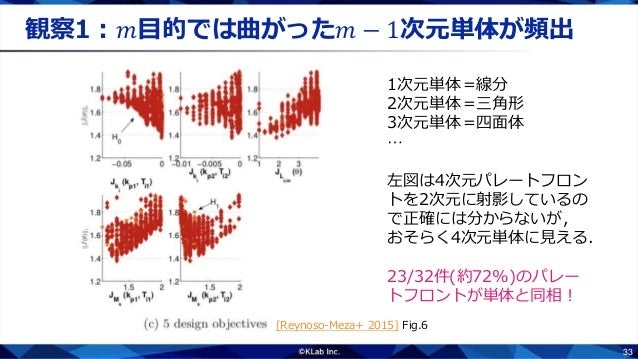
一般に,$m$目的最適化問題のパレートフロントは曲がった$m-1$次元単体になることが多いようです.パレートフロントが掲載されていた実問題32件中23件(約72%)がこのような性質をもっていました.
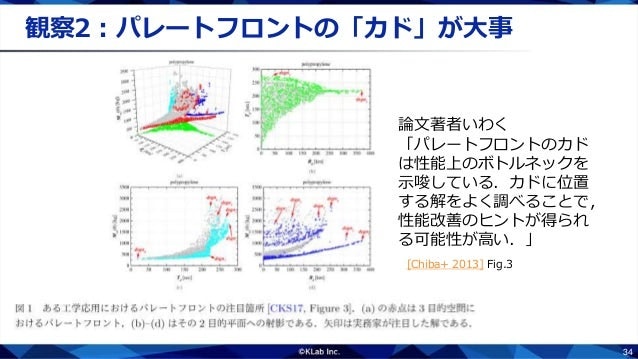
さらにもう一つ大事な観察としては,実務家はしばしばパレートフロントの「カド」に注目するようです.パレートフロントのカドには,パレートフロントがより外側まで伸びることができなかった理由が隠されています.カドを重点的に観察することで,性能上のボトルネックを発見でき,製品設計の改善に繋がるようです.
数学的定式化
では,観察されたこれらの性質を数学的に定義してみます.
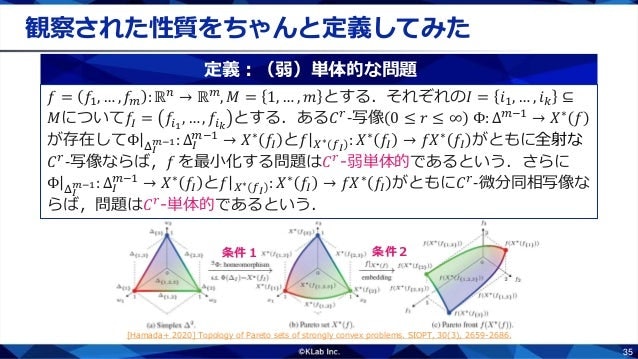
一見難しそうですが,大きく分けて2つの条件からなるということさえおさえておけば大丈夫です.
- 「パレート集合が単体と同相」は,単体$\Delta^{m-1}$からパレート集合$X^\ast(f)$への写像$\Phi$の存在として表されています.$\Phi$が(微分)同相写像であることによって,パレート集合は単体と同相になります.また,$\Phi(\Delta_I) = X^\ast(f_I)$という条件によって,単体の面$\Delta_I$が部分問題のパレート集合$X^\ast(f_I)$に対応することが表されています.
- 「パレートフロントが単体と同相」は,目的関数$f$のパレート集合$X^\ast(f)$への制限$f|_{X^\ast(f)}:X^\ast(f)\to\mathbb R^m$を用いて表されています.この写像が(微分)同相写像であることによって,パレートフロントも単体と同相になります.この写像によって面の構造もパレート集合から誘導されます.
このように,パレート集合とパレートフロントがともに単体と(微分)同相になる問題を単体的な問題と定義します.弱単体的な問題というのは,単体的な問題の条件を少し緩めて,パレート集合やパレートフロントが単体を「つぶした」ような形になるケースです.詳しくは後のスライドで説明します.

歴史のパートでみたように,これまでにも多目的最適化の解集合が何らかの意味で単体であると言及した人はいました.単体的な問題は,それらとどう違うのでしょうか.
第一に,単体の面の構造について厳密に言及したという点が新しいです.Smaleの命題では,「パレート集合は単体と同相」としか言っておらず,面については言及がありません.Lovisonは「$k-1$次元面は$k$目的部分問題のパレート集合」とは言っていますが,どの$k-1$次元面がどの$k$目的部分問題に対応するのかには言及できていません.単体的な問題は,同相写像$\Phi: \Delta^{m-1}\to X^\ast(f)$によって,面$\Delta^{m-1}_I$がパレート集合$X^\ast(f_I)$に対応すると言っています.
第二に,パレート集合だけでなく,パレートフロントにも言及した点が新しいです.これはSmaleとLovisonのどちらにもみられなかったことです.パレート集合が単体なんだから言うまでもなくパレートフロントだって単体になりそうと思いがちですが,そうとは限りません.どちらか一方が単体でも他方が単体でないケースがあります(実際には,それぞれが単体である/ないの2x2通りのケースが存在します).両方が単体になるということにきちんと言及しておく必要があります.
第三に,特定の問題クラスとは切り離して,解集合の性質のみを抽象的に定義したことが新しいです.Smaleの命題は純粋交換経済という経済学の問題に限定されていました.Lovisonは凸最適化問題に限定されていました.単体的な問題の定義は,既存のどの問題クラスにも依存していません.このおかげで,「あるクラスの問題が単体的であるためにはどういう条件が必要か」という議論ができるようになります.
単体的な問題では,部分問題を解くことでパレート集合とパレートフロントの三角形分割が得られます.この性質により,単体的な問題はより複雑な問題のパレート集合やパレートフロントを構成するための「基本部品」になってくれると期待できます.ジェネリックな問題の局所パレート集合や局所パレートフロントは滑層分割集合になることが知られています.ある程度緩い仮定のもとで,局所パレート集合や局所パレートフロントはコンパクトです.任意のコンパクト滑層分割集合は三角形分割可能です.したがって,単体的な問題のパレート集合やパレートフロントを貼り合わせことで,より複雑な問題のパレート集合やパレートフロントを表現することができます.
強凸問題との関係

さて,単体的な問題を定義したので,どんな問題が単体的であるのか気になります.また,単体的であるとわかるとどんなご利益があるのかも知りたいです.そこで,重要な問題クラスである強凸最適化問題が単体的になる条件を調べました.また,単体的な問題の性質を使ってスパースモデリングを効率化する方法を作りました.
強凸問題が単体的である条件
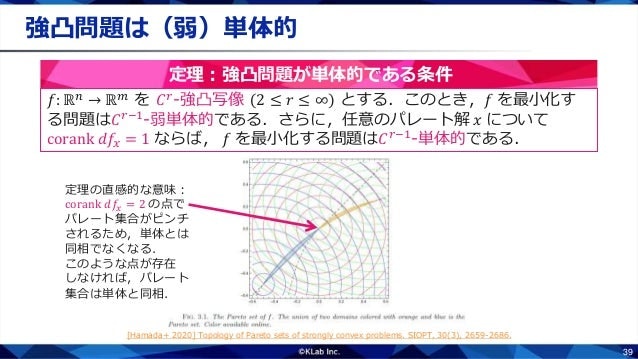
さっそく結果です.2回連続微分可能な強凸最適化問題は常に弱単体的です.弱単体的というのは,スライドの図のように単体的な問題のパレート集合やパレートフロントをつぶしたような形のパレート集合やパレートフロントが生じる問題です.上記の条件に加えて,すべてのパレート解で微分のcorankが1ならば,単体的です.この条件はSmaleの論文ではランク仮定とよばれていたものです.スライドの図では,「つぶれた」点のみがcorank 2で,他のパレート解はみなcorank 1です.corank 2の点が存在しなければパレート集合をつぶすことができなくなり,単体と同相になると理解すればいいと思います.

このランク仮定がどの程度満たしやすい条件なのかが気になります.任意の強凸最適化問題(ただし2回連続微分可能で,$n\ge m$とする)は,ジェネリックな線形摂動を加えればランク仮定を満たすようになります.たとえば,それぞれの目的関数に$\pi(x) = \sum_{i=1}^n \varepsilon_i x_i$($\varepsilon$は微小な乱数)を足せばよいと思います.
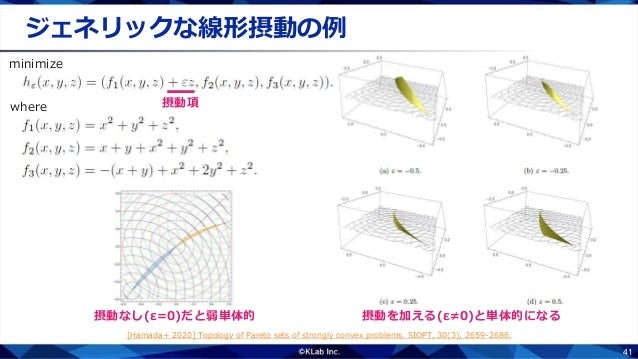
具体例で見てみましょう.さきほどの弱単体的な問題はこのような式で表される問題でした.この第1目的関数に$\varepsilon z$を足すと,弱単体的だった問題が単体的に変わっているのがわかります.
というわけで,強凸という一般的な問題クラスで,Smaleの予想と類似の命題を示せたということは結構よかったかなと思います.
スパースモデリングへの応用
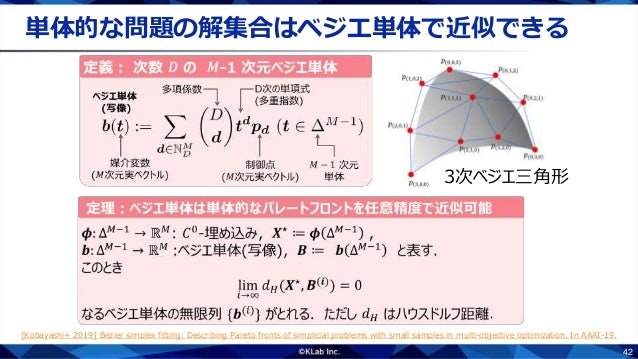
もう一つの成果は,単体的な問題の性質の応用です.単体的な問題のパレート集合とパレートフロントは整った形をしているので,少数の点から全体を近似することが容易です.実際に,ベジエ単体を使うと近似できます.ベジエ単体はベジエ曲線の高次元版で,$n$次元空間内の$m$次元超曲面を表現できます.ベジエ曲線は制御点を動かすことで形状が変わることをご存知だと思います.ベジエ単体も制御点の数が増えただけで考え方は同じです.データに合わせて制御点を調節することで,ベジエ単体をフィッティングすることができます.
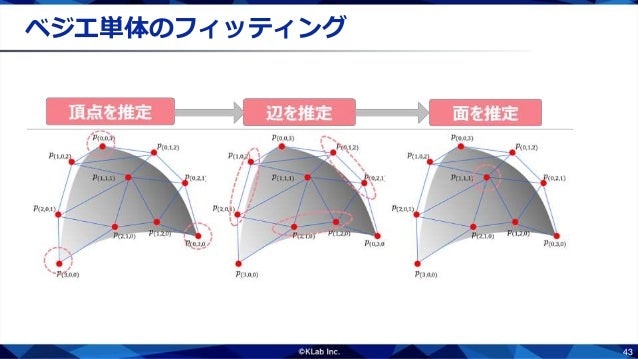
ベジエ単体は,すべての制御点を同時にフィッティングすることもできますが,もう少し効率的なやり方もあります.ベジエ単体の境界は1次元低いベジエ単体で構成されます.たとえば,2次元ベジエ単体(ベジエ三角形)の境界は1次元ベジエ単体(ベジエ曲線)です.1次元ベジエ単体の境界は0次元ベジエ単体(ただの点)です.この性質を利用して,部分単体ごとにフィッテイングできます.頂点,辺,面,…と低次元のベジエ単体から順番にフィッティングしていくことで,一度に動かすパラメータ数を減らすことができ,少ないデータで高精度なフィッテイングが可能となるケースがあります.
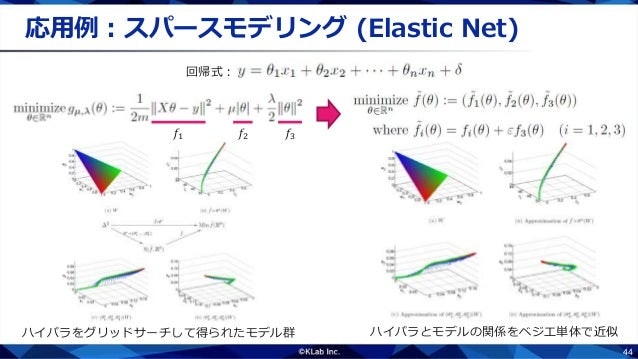
ベジエ単体を使うと,スパースモデリングのハイパーパラメータ調整を効率化できることがあります.たとえば,Elastic Netという手法の損失関数は,線形モデルの誤差項,L1正則化項,L2正則化項の加重和で表されます.ハイパーパラメータである各項の重みを決めて最適化すると,学習済みモデルが得られます.分析するデータに適したハイパーパラメータの値はわからないため,通常はグリッドサーチすることになります.
ベジエ単体を使うと,ハイパーパラメータ空間から学習済みモデル空間への写像を丸ごと近似できます.いくつかのハイパーパラメータで学習するだけで,あらゆるハイパーパラメータで学習したモデルを(近似的に)求めることができます.このようなことはベイズ最適化などでもできますが,ハイパーパラメータ空間の構造を活用しているぶん,より効率的な近似が可能です.
注意:[2021-05-19追記] Elastic Netは$C^0$-強凸最適化問題であるため,$C^2$-強凸最適化問題が弱単体的であるとする先述の定理は適用できません.しかし現在では先述の定理を一般化する研究が進んでおり,任意の$C^0$-強凸最適化問題は弱単体的であることが証明されています.したがって,Elastic Netのパレート集合やパレートフロントはベジエ単体で近似できます. Elastic Netのパレート集合やパレートフロントをベジエ単体で近似できるかどうかは未解決です.Elastic Netは$C^0$-強凸最適化問題であるため,$C^2$-強凸最適化問題が弱単体的であるとする先述の定理は適用できません.しかし,スライドの実験結果を見る限りでは,弱単体的であるように見えます.先述の定理は$C^1$-強凸最適化問題まで拡張されています.もし$C^0$-強凸最適化問題まで拡張できれば,多くのスパースモデリング手法を含むことになるため,非常に有用な定理になると思います.
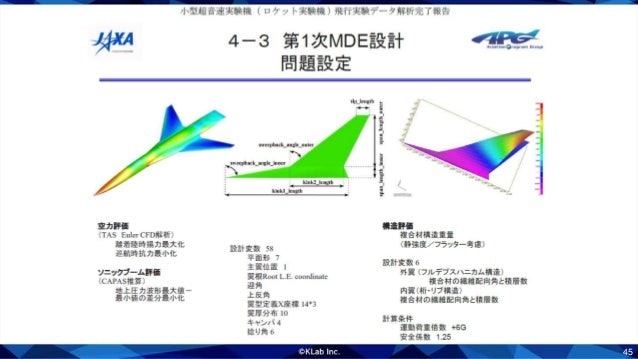
こちらは大規模な設計問題のパレートフロントを近似するために,ベジエ単体を実際に使ってみた例になります.58変数4目的の問題で,パレートフロントのサンプルは58点しかありません.
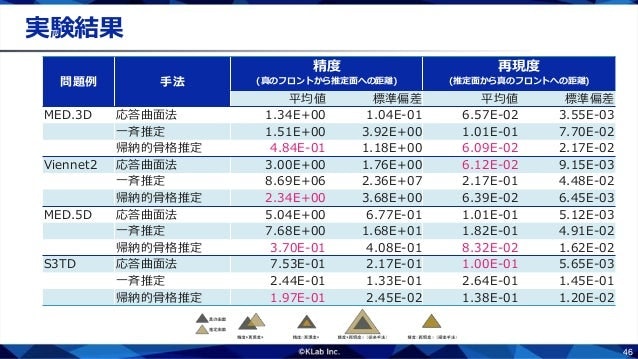
従来この分野でよく使われていた応答曲面法よりも精度よく近似できています.
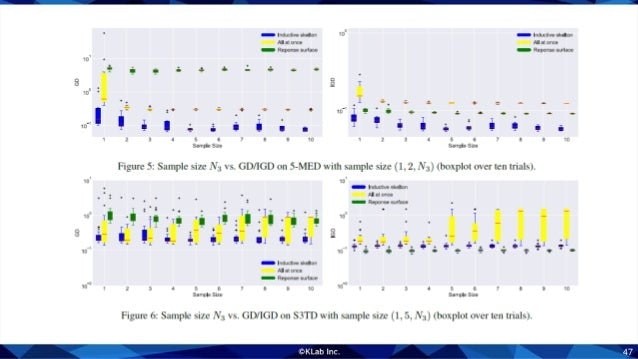
訓練データの数を変化させたときの誤差の推移をみると,少ないデータ数で誤差が収束していることがわかります.たしかにベジエ単体を使うと少数のデータで学習ができるといえそうです.
まとめると,多目的最適化のトポロジー面白いのでもっと流行ってほしいです.
ポアンカレ予想と単体性の検定

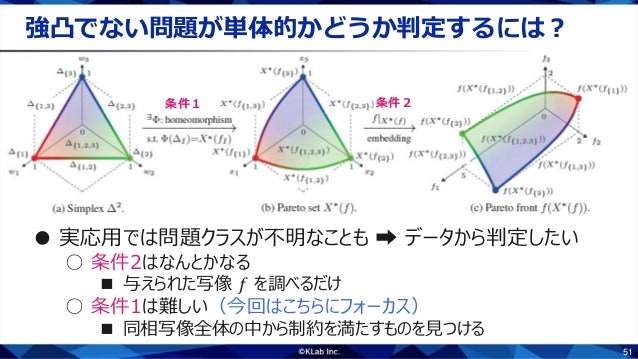
さて,強凸ならばほぼ単体的というのはわかったのですが,問題クラスがわからないケースではどうすればいいのでしょうか?もともと進化計算はブラックボックス最適化をめざしているので,むしろそういうケースのほうが主流です.じつはポアンカレ予想を応用すると,近似解データから単体的かどうかを推定できます.
まず,比較的簡単な,単体的で ない ことを検定する方法から説明します.
実問題では,解の評価にシミュレータを用いることもよくあります.問題の式が与えられないため,問題が強凸なのかどうかは式から判断することができません.問題の性質が事前にわからなくても,進化計算などを用いて,とりあえず近似解データを求めることはできます.もしデータがパレート集合のよい近似になっているならば,データからパレート集合の性質を統計的に推測することはできそうです.
さて,問題が単体的であるためには2つの条件がありました.
- 単体からパレート集合への同相写像$\Phi:\Delta\to X^\ast(f)$で,$\Phi(\Delta_I) = X^\ast(f_I)$を満たすものが存在すること.
- $f|_{X^\ast(f)}$が埋め込みであること.
このうち条件2は具体的な写像が与えられているので,頑張ればチェックできますので今回は割愛します.本発表では特に難しい条件1をデータから推測する方法にフォーカスします.
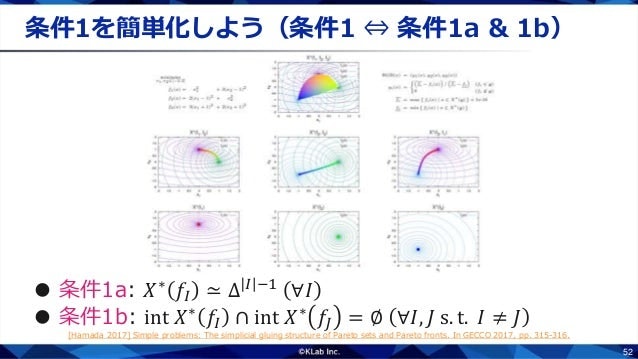
このままでは扱いにくいので,同値な命題に言い換えます.このうち条件1bは比較的簡単なので,条件1aにフォーカスします.単体的で ない ことを示すには,条件1aの否定を示す,つまり,いずれかの部分問題のパレート集合$X^\ast(f_I)$が単体$\Delta^{|I|-1}$と同相でないことを示せば十分です.
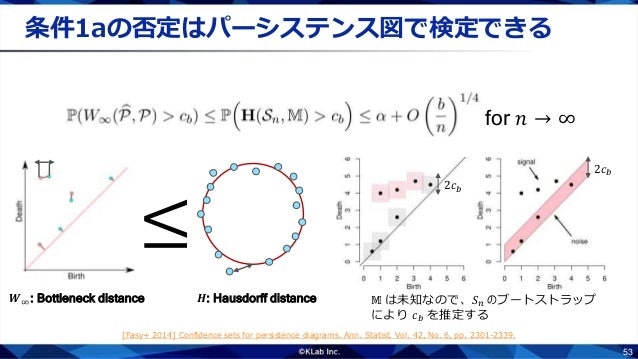
2つの位相空間のホモロジーが同型でないとき,それらの空間は同相ではありません.パーシステンス図を使うと,サンプルからその背後にある位相空間のホモロジーを推定できます.パーシステンス図の点はホモロジー群のサイクルを表しています.対角線付近の赤い領域は信頼区間のようなもので,この領域にあるサイクルは高い確率でノイズであることを示しています.したがって,赤い領域の外側にあるサイクルを数えればホモロジーが推定できます.
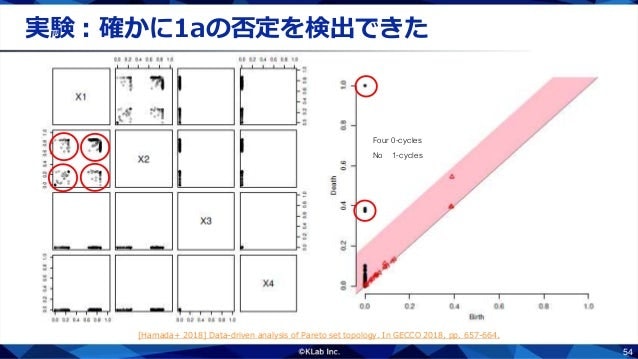
実際のデータで試してみると,パレート集合が4つの連結成分に別れたケースでは,0次のサイクルが4つ生じており,単体のホモロジーと同型ではないことがわかります.したがって,この問題は単体的ではないと推定できます.

位相空間が同相なとき,それらのホモロジーは同型になります.しかし,ホモロジーが同型だからといって,位相空間が同相とは限りません.このせいで,さきほどのパーシステンス図を用いた方法は,単体的で ない ことの検定には使えても,単体的で ある ことの検定には使えないのでした.なんとかして逆向きの推論もできないのでしょうか?

じつは,$n$次元コンパクト多様体$M$とその境界$\partial M$がともに単連結,という仮定をおけば,$M$のホモロジーが$n$次元単体のそれと一致するとき,$M$は$n$次元単体と同相だといえます.ホモロジーはアルゴリズム的に計算できますので,同相問題がアルゴリズム的に解けることになります.ふつう,同相問題は決まった方法で解くことのできない,非常に難しい問題です.単体との同相判定に限られるとはいえ,これはかなりスゴイことです.

証明はとても短いのでここに全部書いておきます.$M$のホモロジーについての仮定から,$H_q(W,\partial_+W)=0$であるとわかります.これをホモロジーの長完全系列に代入すると,$0 \to H_\ast(\partial_+W) \xrightarrow{i_*} H_\ast(W) \to 0$が得られ,包含写像$i:\partial_+W \to W$が誘導するホモロジーの準同型$i_\ast:H_\ast(\partial_+W)\to H_\ast(W)$が同型であると分かります.これに定理4を使うと,$i$がホモトピー同値であることがわかります.$\partial_+$を$\partial_-$に変えて同じ議論を繰り返せます.これらの議論で登場した包含写像がともにホモトピー同値であるとわかったので,定理5より$\partial_+W$と$\partial_-W$は$h$-同境になります.したがって$M$は$\Delta^n$と同相です.□

証明で用いた$n$次元の$h$-同境定理は$n+1$次元のポアンカレ予想と同値です.2003年にペレルマンが3次元ポアンカレ予想を解決するまで,$n=2$のケースは未解決でした.もしこれが未解決のままだったら「いや~この検定法は3目的最適化問題で使えるかどうかまだわからないんです~」って紹介しなければならないところでした.数学の難問の解決は,産業応用上も意味があることだったんですね.
さて,そんなポアンカレ予想ですが,実はまだ解けていないケースが1つだけ残っています.滑らかなカテゴリーでの4次元ポアンカレ予想です.今回紹介した検定法では微分は使っていないんですが,微分が使えればもっと効率的な推定法も作れそうな気がしているので,解けたら嬉しいです.
やっていきましょう.