はじめに
そろそろ
- 機械学習
- AI
- DeepLearning
あたりのことを学ばないとと思い、「ゼロから作るDeepLearning」を読んでみて、まとめとメモを兼ねて書こうかなと。
とりあえず、第1回はパーセプトロンについていきましょう
パーセプトロンとは
パーセプトロン（perceptron）は、ニューラルネットワークやディープラ-ニングにつながる重要な考え方、つまりアルゴリズムです。
簡単にいうと、複数の信号を入力として受け取り、ひとつの信号を出力するというものです。
パーセプトロンの出力信号は、信号を流すか流さないかの2つの値になります。
信号を流す場合を1、流さない場合を0として説明していきます。
2つの入力信号、1つの出力信号のパーセプトロンの例です。
- x1,x2：入力信号
- y：出力信号
- w1,w2：重み
図の○をニューロンやノードと呼びます。
ここで出てきた重みは、入力信号が出力のニューロンに送られる前に計算するのに使います。
w1*x1, w2*x2
この総和が、ある限界値（θ）を超えた場合、出力信号(y)に1が入ります
func perceptron((x1, x2): (Double, Double), (w1, w2): (Double, Double), θ: Double) -> Double {
let sum = w1*x1 + w2*x2
var y
if sum <= θ {
y = 0
} else {
y = 1
}
return y
}
単純な論理回路
AND
| x1 | x2 | y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
2つの入力信号が1の時だけ、出力信号は1になり、それ以外は0になります。
例えば、
func and((x1, x2): (Double, Double)) -> Double {
let w1 = 5
let w2 = 3
let θ = 7
return perceptron((x1, x2): (x1, x2), (w1, w2): (w1, w2), θ: θ)
}
のように値を与えて、表の値をx1とx2に適用して計算すると
// x1 = 0, x2 = 0の例
let y_and = and((x1, x2): (0, 0))
// y_and = 0
yが表の値と全て合うのがわかるかと思います。
NAND
| x1 | x2 | y |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
func nand((x1, x2): (Double, Double)) -> Double {
let w1 = -5
let w2 = -3
let θ = -7
return perceptron((x1, x2): (x1, x2), (w1, w2): (w1, w2), θ: θ)
}
の様な値でNANDを満たします。
OR
| x1 | x2 | y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
func or((x1, x2): (Double, Double)) -> Double {
let w1 = 5
let w2 = 3
let θ = 2
return perceptron((x1, x2): (x1, x2), (w1, w2): (w1, w2), θ: θ)
}
の様な値でORを満たします。
バイアス
perceptronメソッドのコードを少し変更していきます。
// 変更前
func perceptron((x1, x2): (Double, Double), (w1, w2): (Double, Double), θ: Double) -> Double {
let sum = w1*x1 + w2*x2
var y
if sum <= θ {
y = 0
} else {
y = 1
}
return y
}
// 変更後
func perceptron((x1, x2): (Double, Double), (w1, w2): (Double, Double), b: Double) -> Double {
let sum = w1*x1 + w2*x2 + b
var y
if sum <= 0 {
y = 0
} else {
y = 1
}
return y
}
重要な変更点は、バイアス(b)を導入しました。
b = -θとしています。
これにより、sumの値が正か負でyを判断することができます。
XOR
| x1 | x2 | y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
これは、どの様なw1、w2、bを与えても、perceptronメソッドではできません。
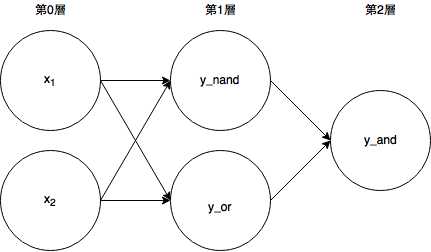
多層パーセプトロン
先ほどXORは実現できませんでした。
しかし、パーセプトロンは1つだけではなく、複数繋げることができます。
func xor((x1, x2): (Double, Double)) -> Double {
let y_nand = nand((x1, x2): (x1, x2))
let y_or = or((x1, x2): (x1, x2))
let y_and = and((x1, x2): (y_nand, y_or))
return y_and
}
この様に、パーセプトロンを組み合わせることで実現できます。
xor((x1, x2): (0, 0)) // 0
xor((x1, x2): (1, 0)) // 1
xor((x1, x2): (0, 1)) // 1
xor((x1, x2): (1, 1)) // 0
試してみると全て、出力が表の通りになっています。
XORの処理を図に表すとこの様になります。
2層まであるため、2層パーセプトロンと呼ばれます。