はじめに
最近は今までライブラリに頼ってブラックボックス化していたものを、一つずつでもなくせるように色々と実装しています。しかしながら、そろそろ勾配降下法の実装や損失関数の微分が面倒になってきました。そんな時に、CVXOPTという最適化ライブラリを見つけたので備忘録としてまとめました。
CVXOPTについて
CVXOPTとは、Pythonで数理最適化問題を解くときに使える便利なライブラリである。具体的には、最適化したい関数が以下のような二次計画問題となっている時、それぞれの値(P, q, A, b, G, h)をCVXOPTの引数に渡すだけで最適解を求めることができる。
\min_{x} \; \frac{1}{2} x^T P x + q^T x \\
\begin{align}
subject \, to \; & Gx \leq h \\
& Ax = b
\end{align}
簡単な二次計画問題
簡単な二次計画問題の例として、以下のような問題をCVXOPTを使って解く。
\min_{x} \; 2x_{1}^2 x_{2}^2 + x_{1}x_{2} + x_{1} + x_{2}\\
\begin{align}
subject \, to \; x_{1} & \geq 0 \\
x_{2} & \geq 0 \\
x_{1}+x_{2} & = 1
\end{align}
この問題を、二次計画問題の定式に当てはめると以下のようになる。
\min_{x} \; \frac{1}{2} \begin{pmatrix} x_{1} \\ x_{2} \end{pmatrix}^T \begin{pmatrix} 4 & 1 \\ 1 & 2 \end{pmatrix} \begin{pmatrix} x_{1} \\ x_{2} \end{pmatrix} + \begin{pmatrix} 1 \\ 1 \end{pmatrix}^T \begin{pmatrix} x_{1} \\ x_{2} \end{pmatrix} \\
\begin{align}
subject \, to \; \begin{pmatrix} -1 & 0 \\ 0 & -1 \end{pmatrix} \begin{pmatrix} x_{1} \\ x_{2} \end{pmatrix} & \leq \begin{pmatrix} 0 \\ 0 \end{pmatrix} \\
\begin{pmatrix} 1 \\ 1 \end{pmatrix}^T \begin{pmatrix} x_{1} \\ x_{2} \end{pmatrix} & = 0
\end{align}
ここまでくると、あとは以下のように、それぞれの値(P, q, A, b, G, h)をCVXOPTの引数に渡すだけで最適解を求めることができる。
from cvxopt import matrix, solvers
# cvxopt専用の行列形式matrixを使う必要あり
P = 2 * matrix([[2, .5],[.5, 1]])
q = matrix([1.0, 1.0])
G = matrix([[-1.0,0.0],[0.0,-1.0]])
h = matrix([0.0,0.0])
A = matrix([1.0, 1.0], (1,2)) # 1 x 2 の形状
b = matrix(1.0)
sol=solvers.qp(P=P, q=q, G=G, h=h, A=A, b=b)
# 最適解を出力
print(sol['x'])
# [ 2.50e-01]
# [ 7.50e-01]
SVMへの応用
次は、CVXOPTを同じ二次計画問題であるSVM(サポートベクターマシン)に応用する。
SVMにおいて解くべき問題は以下のように表され、目的関数$L(a)$を最小化する$a_{i}$を求めることになる。
\min_{a} \; L(a_{1},...,a_{N}) = \frac{1}{2} \sum_{i} \sum_{j} a_{i} a_{j} y_{i} y_{j} k(x_{i}, x_{j}) - \sum_{i} a_{i} \\
\begin{align}
subject \, to \; & 0 \leq a_{i} \leq C \\
& \sum_{i} a_{i} y_{i} = 0
\end{align}
ただし、$x_{i}$はサンプル$i$の特徴ベクトル、$y_{i}$はサンプル$i$のラベル(1 or -1)、$k(⋅,⋅)$はカーネル関数、$C$はハイパーパラメータである。
この問題を、二次計画問題の定式に当てはめると以下のようになる。
\min_{a} \; L(a_{1},...,a_{N}) = \frac{1}{2} a^T KY a + (-1) a \\
\begin{align}
subject \, to \; \begin{pmatrix} I \\ -I \end{pmatrix} a & \leq \begin{pmatrix} C \\ 0 \end{pmatrix} \\
y^T a & = 0
\end{align}
ただし、$Y$は$y_{i}y_{j}$を並べた行列、$K$は$k(x_{i},x_{j})$を並べた行列である。
ここまでくると、あとは以下のように、それぞれの値(P, q, A, b, G, h)をCVXOPTの引数に渡すだけで最適解を求めることができる。
def fit(X, y, C=1.0):
K = rbf_kernel(X) # rbfカーネルを使用
N = len(X)
Y = np.array( [[y[i] * y[j] for j in range(N)] for i in range(N)] )
P = cv.matrix( K * Y )
q = cv.matrix( -np.ones(N) )
G = cv.matrix( np.r_[np.identity(N), -np.identity(N)] )
h = cv.matrix( np.r_[self.C*np.ones(N).T, np.zeros(N).T] )
A = cv.matrix( np.array([y], dtype="double") )
b = cv.matrix(0.0)
sol = cv.solvers.qp(P=P, q=q, G=G, h=h, A=A, b=b)
return sol
補足
SVMの詳しい話は別の記事に委ねるが、SVMの本来の目的は最適解である$a$を使ってデータを予測することである。ちなみに、SVMでは$a$がスパースになることが保証されており、$a_{i}\neq0$であるようなサンプル$i$をサポートベクトルを呼ぶ。
では実際に新しいベクトル$x$をどのように予測するのかというと、
y(x) = \sum_{i \in S} a_{i} y_{i} k(x, x_{i}) + b
\\
b = \frac{1}{N_{s}} \sum_{i \in S} ( y_{i} - \sum_{j \in S} a_{i} y_{i} k(x_{i}, x_{j}) )
と予測する。だたし、$S$はサポートベクトルの集合を表す。
以上を実際の問題に適応すると以下のようになる。問題は、「irisデータを使った2クラス分類」とする。
# irisデータ準備
iris = load_iris()
x_1 = iris.data[iris.target==0, 0:2]
x_2 = iris.data[iris.target==1, 0:2]
x = np.vstack((x_1, x_2))
label_1 = [1 for i in range(x_1.shape[0])]
label_2 = [-1 for i in range(x_2.shape[0])]
label = label_1 + label_2
x_train, x_test, y_train, y_test = train_test_split(x,
label,
test_size=0.2,
random_state=2)
# SVM 学習
## パラメータ初期化
C = 1.0
kernel = rbf_kernel
eps = 10**(-7)
## 最適化
X = x_train
y = np.array(y_train)
K_gram = kernel(X)
N = len(X)
Y = np.array( [[y[i] * y[j] for j in range(N)] for i in range(N)] )
P = cv.matrix( K_gram * Y )
q = cv.matrix( -np.ones(N) )
G = cv.matrix( np.r_[np.identity(N), -np.identity(N)] )
h = cv.matrix( np.r_[C*np.ones(N).T, np.zeros(N).T] )
A = cv.matrix( np.array([y], dtype="double") )
b = cv.matrix(0.1)
sol = cv.solvers.qp(P=P, q=q, G=G, h=h, A=A, b=b)
## サポートベクターの抽出
index_list = list(filter(lambda x: sol['x'][x] > eps , range(N)))
w = np.array(sol['x'])[index_list].reshape(len(index_list)) * y[index_list]
support_vector = X[index_list]
## バイアスの計算
tmp_list = []
for i in index_list:
tmp = 0
for j in index_list:
tmp += (sol['x'][j] * y[j] * K_gram[i][j])
tmp_list.append(y[i]-tmp)
b = np.mean(tmp_list)
# SVM 推論
pred_y = np.dot(np.array([w]), kernel(x_test, support_vector).T) + b
pred_y = pred_y.reshape(len(x_test))
pred_label = np.array([1 if pred > 0 else -1 for pred in pred_y])
print('acc = {}'.format(accuracy_score(y_test, pred_label)))
私の環境では、acc = 1.0となった。
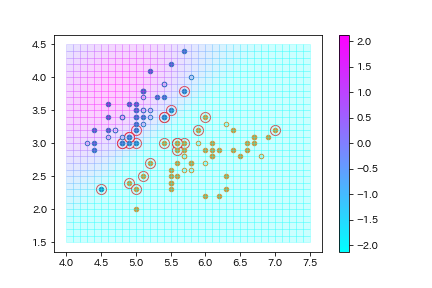
最後に、可視化して確認しておく。きちんと学習・分類ができているようだ。
実点はtrainデータ、白丸はtestデータ、点の2色(青と橙)は2クラス、赤線の囲いはサポートベクトル、背景色はマージンの大きさ($y(x)$)を表す。