ABC089 C - March(300点)

問題概要

問題のリンク

$N$人の人がいる。
以下の条件を満たすように3人選ぶ。

• 全ての人の名前が $M$,$A$,$R$,$C$,$H$ のどれかから始まっている
• 同じ文字から始まる名前を持つ人が複数いない

この時何通りの選び方があるか。ただし選ぶ順番は関係ない。

制約条件

• $1≤N≤10^5$
• $S_i$ は英大文字からなる
• $1≤|S_i|≤10$
• $S_i≠S_j(i≠j)$

考えたこと

先頭の文字が重ならないように選ぶ選び方を考える。

例えば、M,A,R,C,Hから名前が始まる人がそれぞれ1人ずついる場合、以下の選び方で全てであり10通りになる。

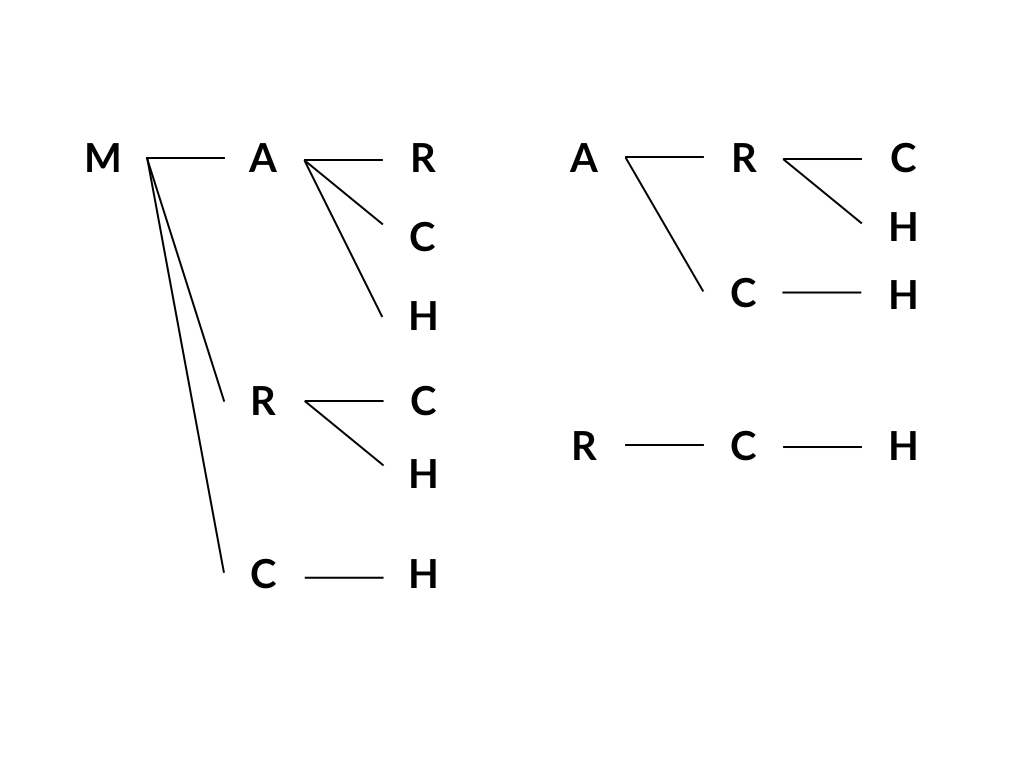
上の図が基本モデルとなる。
まず名前の先頭の文字がM,A,R,C,Hである人の数を数え上げて配列に詰めていく。
重複があってはいけない、かつ選ぶ順番は関係ないので、M,A,R,C,Hを上の図のように組み合わせていき、乗算をしていく。

この時計算量は$O(N)$となるので、問題なくAC。

解答

c.cs

using System;
using System.Linq;

class Program
{
    static void Main(string[] args) {
        int n = int.Parse(Console.ReadLine());
        long[] l = new long[5] {0,0,0,0,0};
        for(int i = 0; i < n; i ++) {
           string s = Console.ReadLine();
           if(s[0]=='M') l[0] ++;
           if(s[0]=='A') l[1] ++;
           if(s[0]=='R') l[2] ++;
           if(s[0]=='C') l[3] ++;
           if(s[0]=='H') l[4] ++;
       }
       Console.WriteLine(solve(l));
    }
    static long solve(long[] l) {
        long count = 0;
        for(int i = 0; i < l.Length-2; i ++) {
            for(int j = i+1; j <= l.Length-2; j ++) {
                count += l[i] * l[j] * (l.Where((x,y) => y > j).Sum());
            }
        }
        return count;
    }
}