先日、こんな記事が上がっていました。
グーグルの天才AI研究者、ニューラルネットワークを超える「カプセルネットワーク」を発表
中々刺激的なタイトルですね。
ニューラルネットワークといえば、近年の機械学習分野を支える最も大きな技術の一つであると言えます。そんなニューラルネットワークを超えたカプセルネットワークとは一体何なのでしょうか。また、本当にニューラルネットワークを超えたのでしょうか。
本記事では、カプセルネットワークの仕組みを理解することで、従来のニューラルネットワークとの違いを比較していきます。
CNN
カプセルネットワークに触れるにあたり、まず**畳み込みニューラルネットワーク(Convolutional Neural Network; CNN)**について理解しなければなりません。なぜなら、カプセルネットワークは、CNNをベースとして、CNNの欠点を克服するために生まれたモデルだからです。
CNNの主要なタスクの一つとして、画像認識が挙げられます。特に2012年にHintonらが提案した深い構造のCNNは、従来の画像認識手法を大きく上回り、その後の画像認識分野に大きな影響を与えました。
CNNは一言で言えば、**「ニューラルネットワーク+局所的受容野+重み共有」**となります。ニューラルネットワークは前提知識として、局所的受容野、重み共有について、次の小節で詳しく見ていきます。
従来のニューラルネットワーク
まずはじめに、従来のニューラルネットワークを用いた画像認識タスクを考えます。
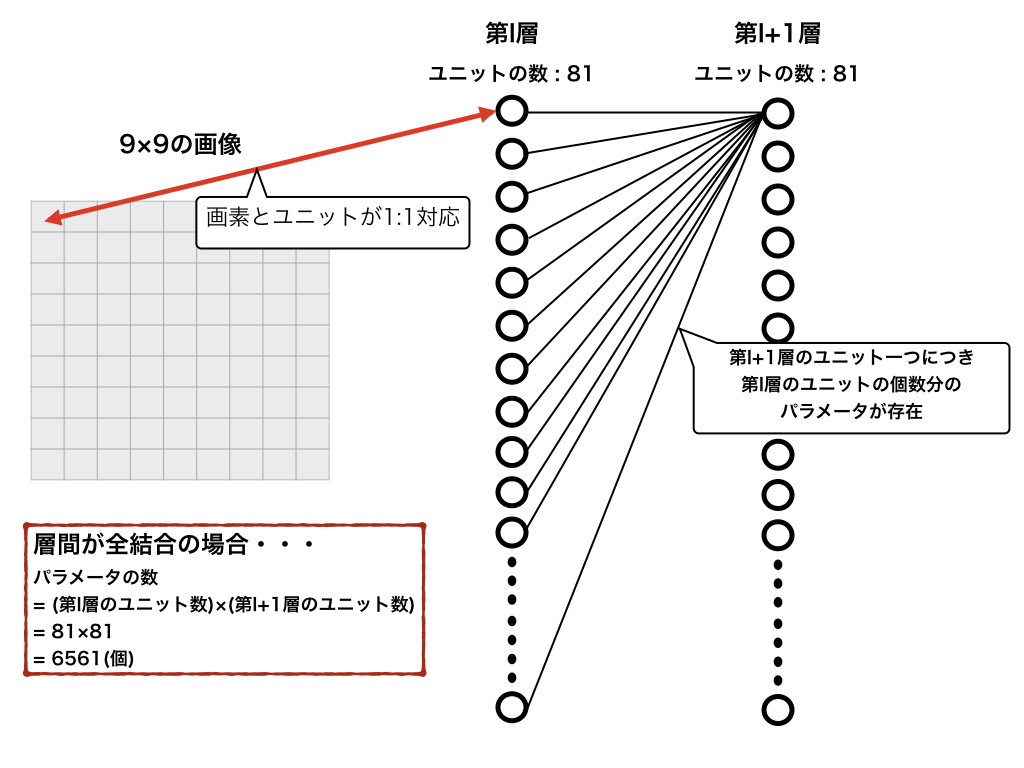
今、例として、サイズが$9\times 9$の画像の第$l$層と第$l+1$層の重みを求めるとします。ただし、以降では第$l$層と第$l+1$層のユニットの数は同じものとします。(実際は、異なる場合が多いですが、説明のため。)
この時、層が**全結合(fully-connected)**であると仮定すると、学習すべきパラメータの数は次のようになります。
ここでは、$9\times 9$と非常に小さい画像を例として挙げましたが、実際には$28\times 28$、$1000\times 1000$などの画像に対して、処理を行いたいことがしばしばあります。その時のパラメータの数は、以下のようになります。
- $28\times 28$の画像の全結合層のパラメータの数: ($l$層) $784$ $\times$ ($l+1$層) $784$ $=$ $614656$
- $1000\times 1000$の画像の全結合層のパラメータの数: ($l$層) $1000000$ $\times$ ($l+1$層) $1000000$ $=$ $1000000000000$($1$兆)
これから見てわかるように、画像はその膨大な情報量から、ニューラルネットワークをそのまま適用するには、パラメータの数があまりにも膨大になりがちです。
これでは、普通のcpuでは、何百年、何千年かかっても計算が終わりませんね。
局所的受容野
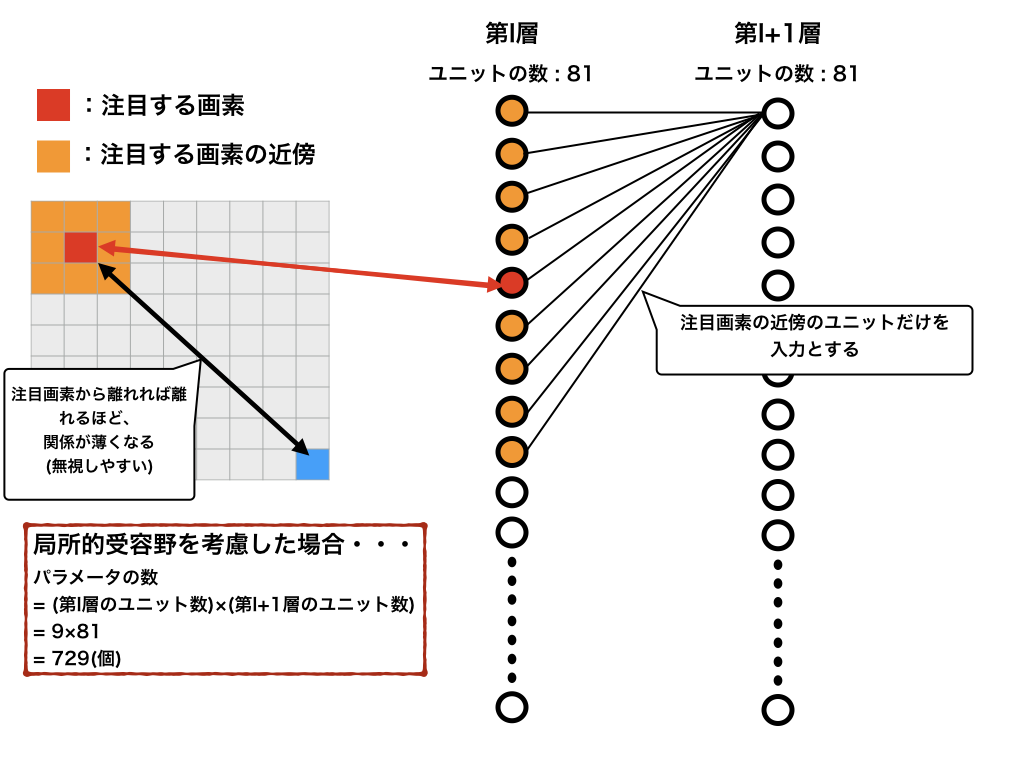
このような問題を克服するために考えられたのが、**局所的受容野(local receptive field)**という考え方です。一般に、ある画像の注目点を考える時、その注目点の近傍の点は関係が強く、離れていけば離れるほど関係が薄いということが想像できると思います。それを利用して、次の層への入力を近傍のユニット群だけとするのが局所的受容野の考え方です。
上図では、注目点の周りの$8$画素を近傍と仮定しています。このように、層と層の間が全結合していたものが、層の中でも特に関係が強いユニット(=画素)のみを結合させることができます。これより、パラメータの数を大幅に減らすことができます。
他の画像サイズのパラメータの数は次のようになります。(端の画素の周囲の8画素はどうなるの?という方はpaddingなどで調べると良いでしょう)
- $28\times 28$の画像のパラメータの数: ($l$層) $9$ $\times$ ($l+1$層) $784$ $=$ $7056$
- $1000\times 1000$の画像のパラメータの数: ($l$層) $9$ $\times$ ($l+1$層) $1000000$ $=$ $9000000$
このように、かなりパラメータの数が減ったことが見て取れます。
重み共有
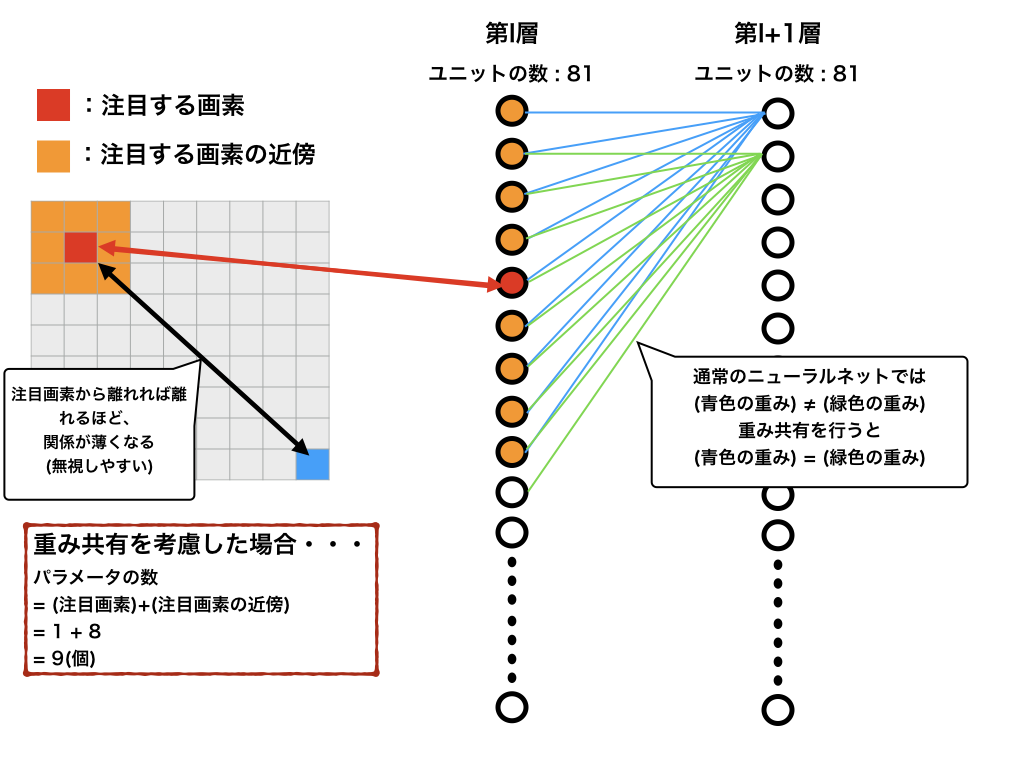
さらに、パラメータの数を減らす工夫として、**重み共有(weight sharing)**という手法が知られています。これまでは、各注目点ごとに別々の重みを求めていましたが、画像の一部で有効な特徴抽出は他の部分でも有効である場合があります。それを利用して、層間の重みを同様のものを用いることを重み共有と言います。
上図から、学習すべきパラメータをさらに減少させることに成功していることがわかります。
- $28\times 28$の画像のパラメータの数: 9個
- $1000\times 1000$の画像のパラメータの数: 9個
これにより、複数の特徴マップを作成することができ、画像から豊かな情報を取り出すことができます。
プーリング
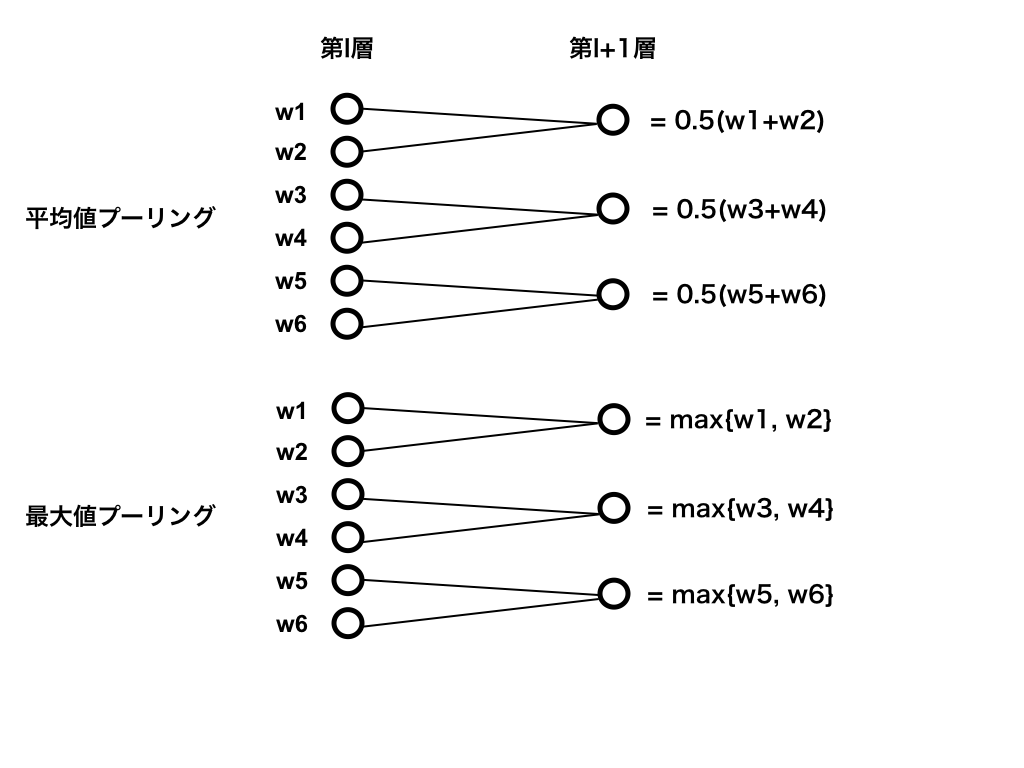
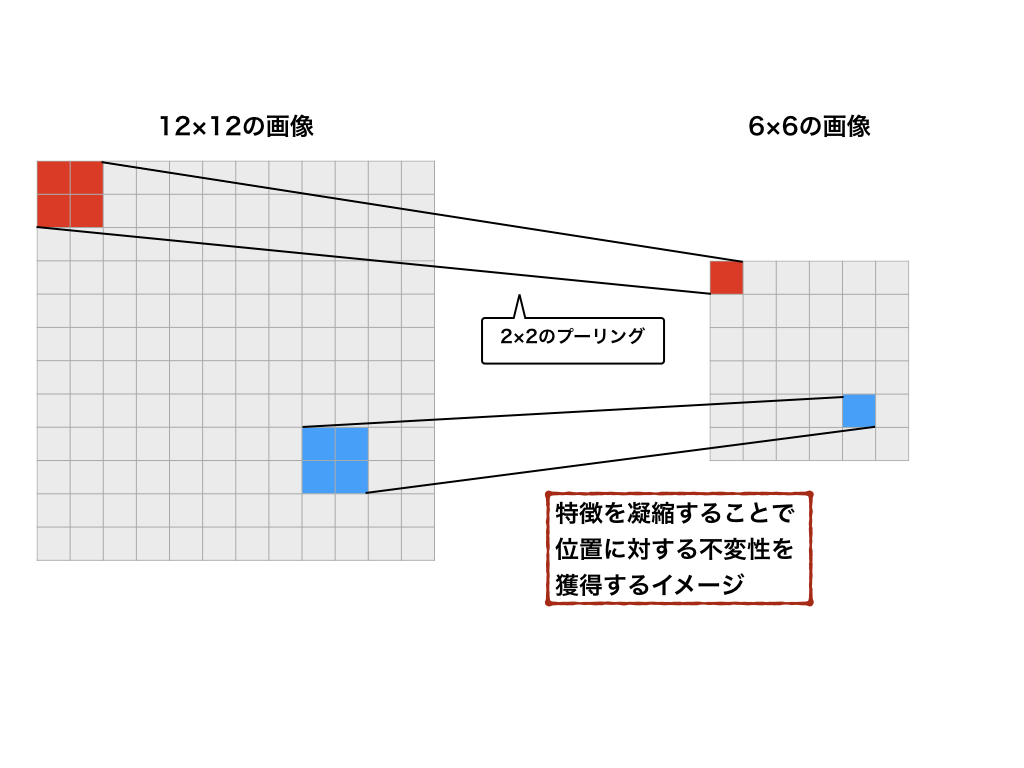
また、CNNでは上記の二つを合わせた畳み込み層に加え、**プーリング層(pooling layer)**と呼ばれる層がよく用いられます。画像から特徴を抽出するとき、画像の局所的なゆがみや平行移動の影響を受けにくい不変性を持つことが期待されます。プーリング層では、特徴量の統計量を計算することで、こういった変化に対して頑健性を保証します。
上図のように、より特徴を際立たせることで、微小な位置の変化や平行移動に対する不変性を獲得することができます。画像でイメージすると、よりわかりやすいと思います。
これをプーリング層と呼び、この畳み込み層とプーリング層を重ねることにより、画像認識タスクを解くことが一般的です。
次の図は、手書き文字認識タスクとして有名なLeNet[2]のネットワーク図となります。

このように実際に用いられるネットワークは、畳み込み層とプーリング層を複数重ね合わさせた構造を持ちます。
CNNの欠点
さて、それではCNNの欠点とはどういったところにあるのでしょうか。
まず、カプセルネットワークを提案したHintonの言葉を借りましょう。
Hinton: “The pooling operation used in convolutional neural networks is a big mistake and the fact that it works so well is a disaster.”
簡単に言えば、CNNで用いられているプーリングという操作が大きな過ちであると言っています。
では、プーリングの何が過ちなのでしょうか。それは、プーリングにより位置不変性を獲得すると同時に、空間的な構造の情報を喪失していることを指します。
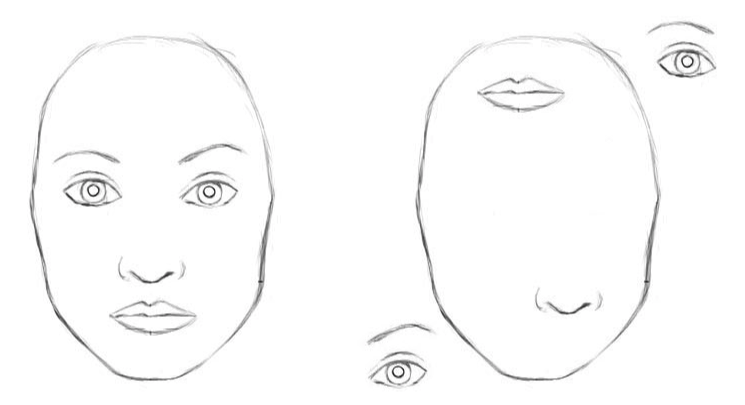
具体的に、次の図([4]より)を見るとわかりやすいでしょう。
左の図は人の顔をあらわしており、右の図は顔のパーツを適当に配置し直した図となります。人間にとっては、右は明らかに普通の顔でないことがわかりますが、CNNはこの二つの図を同じものとして認識してしまいます。なぜなら、右の図には、(位置はともかく)目、鼻、口が存在しているからです。
このように、プーリング層は位置不変性を頑健なものとする一方、画像の空間的な情報を考慮することができません。位置不変性について詳しく知りたい方は、SIFT記述子などで調べると良いかもしれません。
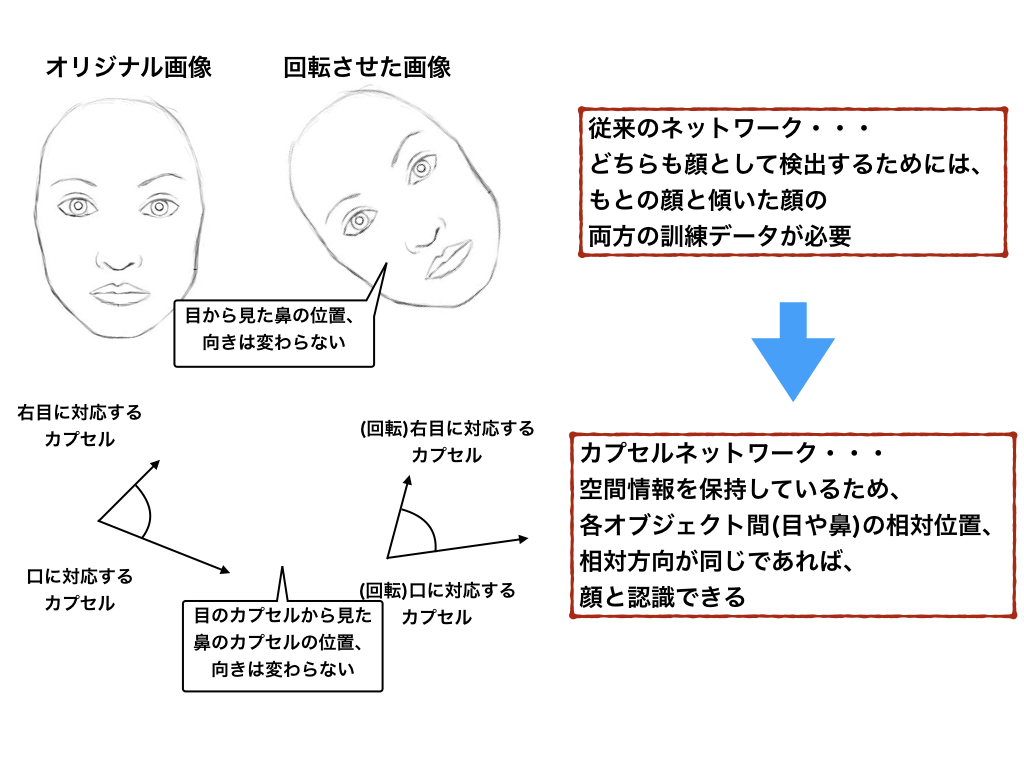
また、CNNは回転や比率の変わった画像認識を行うために、膨大な訓練データを必要とするという欠点も挙げられます。
例えば、次の図を見てみましょう。
これは様々な角度から撮った自由の女神像ですが、人間が見るとすぐに同一のものと認識できます。しかし、CNNにその能力は存在しません。CNNでは、空間的な情報を考慮することができないため、これを同一のオブジェクトと認識するためには、それぞれの角度から撮った自由の女神像の訓練データを大量に必要とします。
そこで、こういった欠点を克服しようとしたものが、次節のカプセルネットワークとなります。
CapsNet
**カプセルネットワーク(Capsule Network; CapsNet)**は、深層学習の偉大な貢献者の一人であるHintonらが公開した論文、"Dynamic Routing Between Capsules"で提案されたモデルです。 (最初に"カプセル"という言葉が出たのは2011年の論文ですが。)
では、カプセルネットワークとは一体何なのでしょうか。CNNの欠点で見てきた通り、プーリングは様々な情報、特に特徴間の空間的な関係(目と顔、目と鼻の相対位置など)を失ってしまいます。そこで、カプセルネットワークでは、従来のニューロン(ここまでユニットとして表現していたもの)が一つのスカラー値を出力として持つのに対し、空間情報をベクトルとして出力します。これを、カプセルと呼びます。
次節で、この違いを詳しく見ていきます。
カプセルとニューロンの違い
カプセルとニューロンの主要な違いをまとめたものが、以下の表([4]より)となります。
まず、ニューロンについておさらいです。ニューロンは、他のニューロンからスカラーを受け取り、それぞれ重みを掛け合わせ、最後に足し合わせていました。こうして得られたスカラーは非線形の活性化関数を通り、スカラーの出力を生みます。このスカラーが、ニューロンのアウトプットとして出力され、さらに次の層への入力として用いられます。これをまとめると、次のようになります。
- 入力スカラーへスカラーで重み付け
- 重み付けされた入力スカラーの和
- スカラーからスカラーへの非線形変換
カプセルネットワークでは、スカラーの代わりにベクトルを用い、さらに上の3ステップにアフィン変換のステップを加えます。
- 入力ベクトルと行列の積
- 入力ベクトルへスカラーで重み付け
- 重み付けされた入力ベクトルの和
- ベクトルからベクトルへの非線形変換
これをまとめたのが、以下の図([3]より)となります。

左がカプセル、右が従来のニューロンをあらわしています。図中での、${\bf u}$がベクトルをあらわしていることに注意してください。カプセルにおいて注目するべき点は、以下の点です。
- 入力/出力がともにベクトルである
- アフィン変換のステップが加えられている
- 活性化関数がsquah関数(後述)で置換されている
- バイアスがない
次節以降では、それぞれのステップの役割を見ていきます。
入力ベクトルと行列の積
カプセルが受け取る入力ベクトル(図中での${\bf u}_i(i=1,2,3)$)は、前の層の3つの他のカプセルから来ています。これらのベクトルの大きさが、カプセルに対応するオブジェクトが存在する確率をあらわし(例えば、目に対応するカプセルであれば、そのカプセルのノルムが目の存在確率をあらわす)、ベクトルの向きがそのオブジェクトの空間的な情報をあらわします。ここでは、高いレベルのカプセルが顔を検知し、低いレベルのカプセルが目、鼻、口を検知するものとします。
はじめに、これらのベクトルは、対応する重み行列$W$が掛けられます。これは、空間的な情報と高いレベルのカプセル(顔)と低いレベルのカプセル(目、鼻、口)の関係を結びつけます。例えば、$W_{2j}$は、鼻と顔の関係性、顔の中心に鼻があることや顔は鼻の10倍程度の大きさがあること、顔の向きと鼻の向きが同じであることなど、をあらわします。
こうして得られたベクトルは、高いレベルの特徴と結びつけられた新たな特徴が得られます。例えば、$\hat{{\bf u}}_1$は、検出された目に対してどこに顔があるべきか、などをあらわします。
空間情報を保持しているイメージは次の図の通りとなります。(元画像はこちら)
入力ベクトルへスカラーで重み付け
このステップは、従来のニューラルネットワークの重み付けと非常によく似ています。従来のネットワークでは、この重みはバックプロパゲーションを用いて、学習されるのが一般的です。しかし、カプセルでは"dynamic routing"と呼ばれる手法を用いて学習させます。ルーティングという言葉からわかるように、前の層のカプセルから次の層のどのカプセルへどれだけの重みを配分するかを決定します。
ここでは、重みを$c_{ij}$とします。ただし、$i$は$l$層に含まれるカプセルをあらわし、$j$は$l+1$層に含まれるカプセルをあらわします。
全体のルーティングアルゴリズムは次のようになります([5]より)。

ここで、重み$c_{ij}$は、ソフトマックス関数を用いて次のようにもとめられます。
$$
c_{ij} = \frac{{\rm exp}(b_{ij})}{\sum_{k}{\rm exp}(b_{ik})}
$$
$c_{ij}$は、$j$に関して和をとると、合計が$1$になることがわかります。(ゆえに、ルーティングと呼ばれます。)
$b_{ij}$は、はじめ$0$で初期化され、次のように更新されます。
$$
b_{ij} \leftarrow b_{ij} + \hat{{\bf u}}_{j|i} \cdot {\bf v}_{j}
$$
ここで、$\hat{{\bf u}}_{j|i} \cdot {\bf v}_{j}$は"agreement"と呼ばれ、この値が大きいほど重みが大きくなります。これは、入力カプセルと出力カプセルがどの程度似ているものかをあらわします。
重み付けされた入力ベクトルの和
このステップは、通常のニューロンと非常によく似ています。通常のニューロンでは、重み付けされたスカラー値を足し合わせますが、カプセルでは、入力がベクトルとなるので、重み付けされたベクトルを足し合わせます。
ベクトルからベクトルへの非線形変換
カプセルネットワークの革新の一つとして、活性化関数をsquash関数へ置換した点が挙げられます。
squash関数を適用すると、入力をベクトル${\bf s}$としたとき、その出力ベクトル${\bf v}$は次のようにあらわされます。
$$
v = \frac{||s||^2}{1+||s||^2} \frac{s}{||s||}
$$
ここで、注意しなければならないのは、入力と出力の向きは変わらない、という点です。squash関数は、向きを変えず、$1$を超えないように大きさをスケーリングします。この出力ベクトルの長さが、カプセルと対応する特徴量が存在する確率として解釈されます。
式の右部分
$$
\frac{s}{||s||}
$$
は、ベクトル${\bf s}$を大きさ$1$にスケーリングしています。
式の左部分
$$
\frac{||s||^2}{1+||s||^2}
$$
は、単位ベクトルをさらに押しつぶす(squash)スケーリングです。${\bf s}$の大きさにより、
$$
\frac{||s||^2}{1+||s||^2} \rightarrow 0 ,, (||s||\rightarrow 0) ,, , \frac{||s||^2}{1+||s||^2} \rightarrow 1 ,, (||s||\rightarrow \infty)
$$
となります。
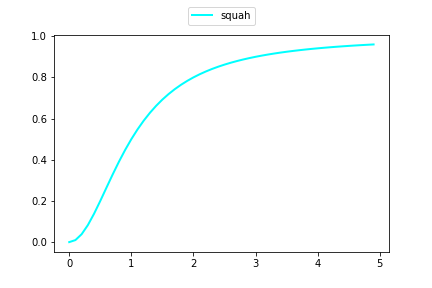
すなわち、${\bf s}$が大きければ大きいほど単位ベクトルそのものに近づき、小さければ小さいほど零ベクトルに近づきます。squash部分は、横軸を入力スカラーとすると、次のような非線形スケーリングを行います。
カプセルまとめ
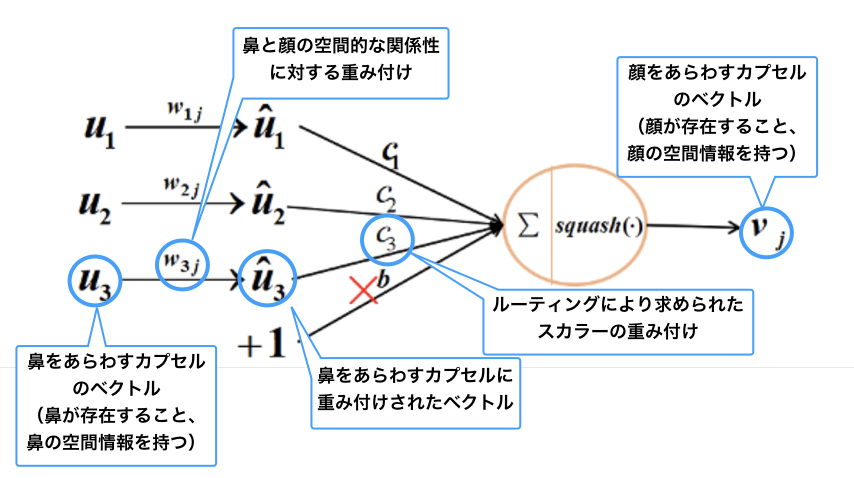
以上をまとめると、次の図のようになります。
かなりカプセルの正体に近づけた気がしますね。
ここまでカプセルについて見てきましたが、カプセルの大きな特徴の一つとして、プーリングで失われていた空間情報を保持する、という点が挙げられます。
実際、論文では複数の手書き文字を重ね合わせたMultiMNISTデータセットに対して、良い精度を示しています。しかし、計算速度やMNIST以外のデータセットでの検証など、まだまだカプセルネットワークがニューラルネットワーク(というよりCNNでしょうか)を超えた、というのは、個人的には早計な気がしています。
とはいえ、空間情報の保持という非常に強力な特性を持ったカプセルネットワークの発展は、非常に期待が持てますね。
実装が気になる方は、[1]でコメント付きのカプセルの実装が行われているのでそちらをご覧ください。
まとめ
ここまで読んでいただいた方、ありがとうございました。
記事中の式、数値は実際計算を行いましたが、大きく間違っているなど、お気付きの点、またご感想がありましたら、遠慮なくコメントやTwitterの方でお声がけください。
参考
[1] Debarko De, "What is a CapsNet or Capsule Network?", 2017, Available at https://hackernoon.com/what-is-a-capsnet-or-capsule-network-2bfbe48769cc.
[2] Yann LeCun, Leon Bottou, Yoshua Bengio and Patrick Haffner, "Gradient-Based Learning Applied to Document Recognition", IEEE, 1998, Available at http://yann.lecun.com/exdb/publis/pdf/lecun-98.pdf.
[3] Huadong Liao, "CapsNet-Tensorflow", 2017,Available at https://github.com/naturomics/CapsNet-Tensorflow.
[4] Max Pechyonkin, "Understanding Hinton’s Capsule Networks. Part I: Intuition.", 2017, Available at https://medium.com/ai%C2%B3-theory-practice-business/understanding-hintons-capsule-networks-part-i-intuition-b4b559d1159b.
[5] Sara Sabour, Nicholas Frosst, Geoffrey E Hinton, "Dynamic Routing Between Capsules", NIPS(2017), 2017, Available at https://arxiv.org/pdf/1710.09829.pdf.
[6] Tom Simonite, "グーグルの天才AI研究者、ニューラルネットワークを超える「カプセルネットワーク」を発表", WIRED, 2017, Available at https://wired.jp/2017/11/28/google-capsule-networks/.