はじめに
今回は、LLM 分野のブレイクスルーとなった Transformer に関する論文 "Attention Is All You Need" を紹介します。このモデルは、 Attention のみを利用しており、従来の RNN や CNN ベースのモデルを置き換える新しいアプローチとして注目を集めました。正直、有名な論文過ぎて今更感もありますが、名作は色あせないと思いますので、論文の主な貢献点を簡潔に紹介し、数式を交えながら新しく導入された Attention の詳細を説明します。
参考文献:
A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, Ł. Kaiser, & I. Polosukhin. (2017). Attention Is All You Need. Advances in Neural Information Processing Systems, 30.
🐣 見出し最初の数字が元論文の章に対応していますが、数式番号は論文とは独立です
1, 2 論文の概要
当時、主流だった RNN ベースの seq2seq モデルには並列化できない制約がありました。また、長期記憶を保持しきれないという問題もありました。そこで Attention だけに基づく新手法 Transformer を提案します。RNN や CNN を完全に省いた初のモデルでありながら、翻訳タスクで当時世界最高の結果を得ることができました。
3 Transformer の構造

図1: Transformer モデルのアーキテクチャ。エンコーダー(左)とデコーダー(右)から構成されている。(出典:Vaswani et al., "Attention Is All You Need," 2017)
🐣 世界で一番有名なネットワーク構造の図かもしれないですね
Transformer はエンコーダーとデコーダーからなる典型的な構造を持ちます。これにより、高度な並列処理が可能となり、従来のリカレントモデルを凌駕する性能を発揮します。
3.2 Transformer における Attention
Transformer は、以下に示す基本的な注意機構 (attention mechanism) である Scaled Dot-Product Attention と、それを並列に束ねた構造である Multi-Head Attention を核として構成されています。
またこれ以降の説明は、エンコーダーにおける自己注意 (Self-Attention) についての説明になります。

図2左: Scaled Dot-Product Attention。Transformer の中核をなす構成要素。(出典:Vaswani et al., "Attention Is All You Need," 2017)
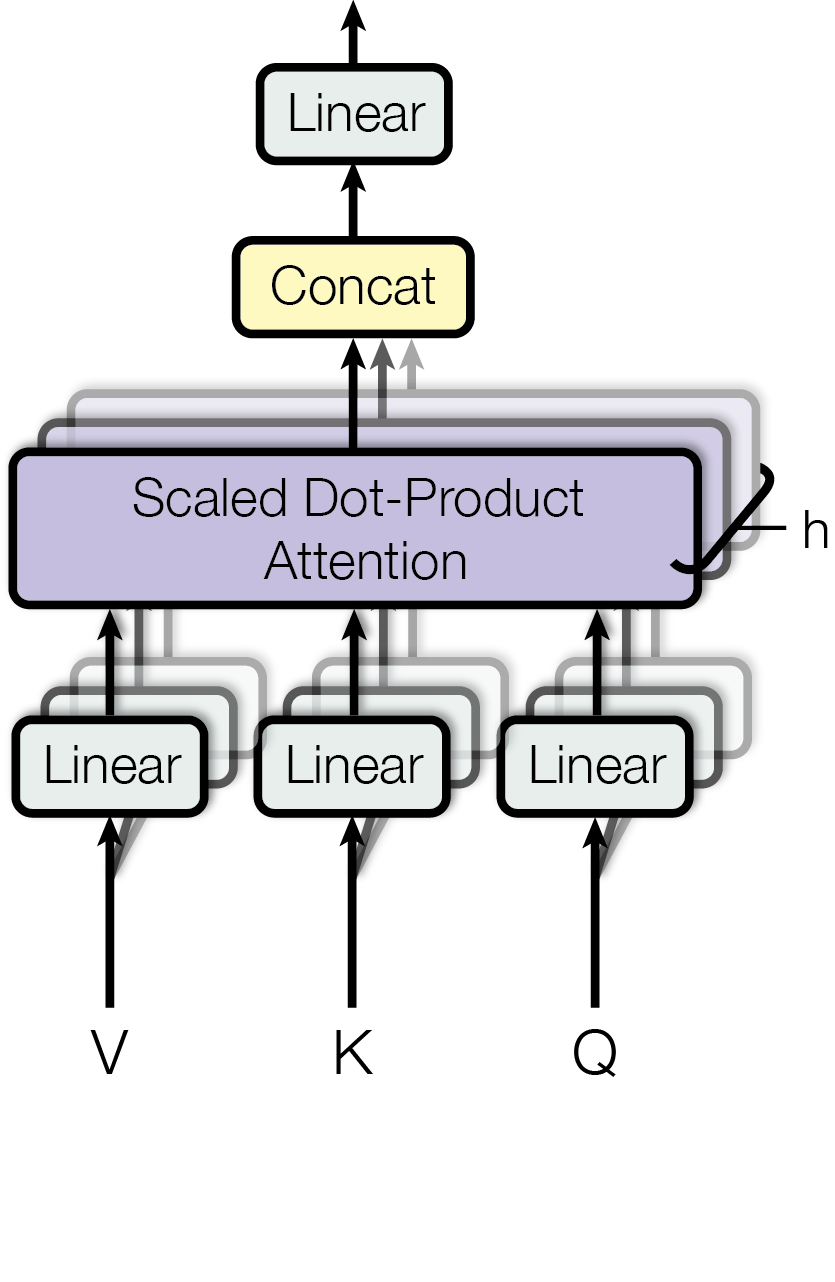
図2右: Multi-Head Attention。Scaled Dot-Product Attention を複数並列に束ねた構造であり、各 Scaled Dot-Product Attention は Head と呼ばれる。(出典:Vaswani et al., "Attention Is All You Need," 2017)
3.2.1 Scaled Dot-Product Attention
Scaled Dot-Product Attention は、query $Q$、key $K$、value $V$ の 3 つのベクトルを用いて計算されます。それぞれ次の次元を持ちます。
- $Q \in \mathbb{R}^{n \times d_k}$
- $K \in \mathbb{R}^{n \times d_k}$
- $V \in \mathbb{R}^{n \times d_v}$
ここで:
- $n$: シーケンス長(入力トークン数)
- $d_k, d_v$: key と value の次元
$Q, K, V$ は入力埋め込み(行列 $X \in \mathbb{R}^{n \times d_{\text{model}}}$)から以下のように生成されます。
$$
Q = X W^Q, \quad K = X W^K, \quad V = X W^V
$$
ここで $W^Q, W^K, W^V \in \mathbb{R}^{d_{\text{model}} \times d_k}$ は学習可能な重み行列です。
Attention の計算式は以下の通りです。
$$
\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^\top}{\sqrt{d_k}}\right)V \tag{1}
$$
この操作により、query $Q$ が特定の key $K$ にどれだけ関心を持つべきか(スコア)を求め、そのスコアに基づいて value $V$ を線形結合で更新します。
特徴
- 並列化: 全トークン間の依存関係を一度に計算可能
- 長距離依存関係: トークン間の関係を効率的にモデル化
3.2.2 Multi-Head Attention
Multi-Head Attention は、Scaled Dot-Product Attention を複数並列に束ねた構造であり、各 Scaled Dot-Product Attention はヘッド (Head) と呼ばれます。この構造により、異なる表現空間から多様な注意を同時に学習することが可能になります。
大まかな動きとしては、入力された $V$、$K$、$Q$ を各 Head ごとに異なる線形層で変換した後、それぞれの Head で Scaled Dot-Product Attention を計算します。最後に、次式のように各 Head の出力を Concat で結合し、最終的な線形変換を施して出力を得ます。
$$
\text{MultiHead}(Q, K, V) = \text{Concat}(\text{head}_1, \dots, \text{head}_h)W^O \tag{2}
$$
ここで各 Head、つまり Scaled Dot-Product Attention は以下のように計算されます。
$$
\text{head}_i = \text{Attention}(QW_i^Q, KW_i^K, VW_i^V) \tag{3}
$$
ここで、$W_i^Q, W_i^K, W_i^V \in \mathbb{R}^{d_{\text{model}} \times d_k}$ および $W^O \in \mathbb{R}^{h d_k \times d_{\text{model}}}$ は学習可能な重み行列です。
具体的には次の式で計算されます。
$$
\text{Attention}(QW_i^Q, KW_i^K, VW_i^V) = \text{softmax}\left(\frac{QW_i^Q (KW_i^K)^\top}{\sqrt{d_k}}\right)VW_i^V
$$
特徴
- 多様性の確保: 各 Head が異なる情報を学習可能。
- モデルの頑健性: 複数の空間での Attention により、より表現力豊かなモデルを実現。
補足: 論文中のモデルにおける具体的な次元数
-
モデル全体の次元:
- $d_{\text{model}} = 512$(入力埋め込みや出力埋め込みの次元数)
-
$Q$ と $K$ の次元:
- $d_k = 64$(key と query の次元数)
-
$V$ の次元:
- $d_v = 64$(value の次元数)
🐣 $Q$ と $K$ は内積を取るため同次元が必要ですが実は $V$ は別でも構いません
-
Head の数:
- $h = 8$(Multi-Head Attention 内の Head 数)
-
シーケンス長:
- 入力トークン数 $n$ はタスクに依存します。例えば、翻訳タスクではシーケンス長は最大 50 トークンと仮定して以下の表では $n = 50$ としています。
| 成分 | 次元 | 数値 |
|---|---|---|
| $X$ (入力埋め込み) | $\mathbb{R}^{n \times d_{\text{model}}}$ | $\mathbb{R}^{50 \times 512}$ |
| $W^Q, W^K, W^V$ | $\mathbb{R}^{d_{\text{model}} \times d_k}$ | $\mathbb{R}^{512 \times 64}$ |
| $Q, K$ | $\mathbb{R}^{n \times d_k}$ | $\mathbb{R}^{50 \times 64}$ |
| $V$ | $\mathbb{R}^{n \times d_v}$ | $\mathbb{R}^{50 \times 64}$ |
| スコア行列 | $\mathbb{R}^{n \times n}$ | $\mathbb{R}^{50 \times 50}$ |
| Attention 出力 | $\mathbb{R}^{n \times d_v}$ | $\mathbb{R}^{50 \times 64}$ |
| マルチヘッド 結合後 | $\mathbb{R}^{n \times (h \cdot d_v)}$ | $\mathbb{R}^{50 \times 512}$ |
| 線形変換後の出力 | $\mathbb{R}^{n \times d_{\text{model}}}$ | $\mathbb{R}^{50 \times 512}$ |
3.5, 3.6 Transformer の入力処理
次は入力について見ていきましょう。
- テキストの変換
- サブワード単位でトークン化(BPE 等)して ID に変換
-
[SOS]、[EOS]等の特殊トークンを追加 - ボキャブラリサイズは 3~4 万程度
🐣 SOS は Start of Sequence、EOS は End of Sequence の略です。助けて~じゃありません!
- ベクトル化
-
トークン ID を埋め込みベクトルに変換(512 次元)
-
サイン・コサイン波による位置エンコーディングを加算(式 (5), (6))
$$
PE_{(pos, 2i)} = \sin\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right)
$$
$$
PE_{(pos, 2i+1)} = \cos\left(\frac{pos}{10000^{2i/d_{\text{model}}}}\right)
$$
これで、位置情報を含む固定長ベクトル系列として扱えるようになります。単純にベクトルとして加算されるため、同一トークンでも異なる位置に現れると微妙にベクトルの内容が異なることになります。
補足: Skip-Connection と V 空間の縮小防止
問題点: 空間の縮小
Scaled Dot-Product Attention の出力は、$Q$ と $K$ に基づく加重平均によって $V$ 全体の線形和になります。この操作では、各トークンが他のすべてのトークンに依存する形で情報を集約します。その結果、情報が圧縮される傾向があり、操作を繰り返すうちに $V$ の空間が単一の方向に収束する可能性があります。
また、論文の式 (2) の Multi-Head Attention では、各 Head が独立に異なる情報を学習する設計ですが、最終的にはすべての Head の出力を結合 (Concat)して線形変換を施します。このとき、$V$ の影響もあり、この操作を繰り返すうちにモデル全体の表現力が減少する可能性があります。
解決策: 残差接続 (Skip-Connection)
論文では、これに対して Multi-Head Attention の出力に元の入力($X$)を加える残差接続を採用しています。この手法により、Scaled Dot-Product Attention で仮に $V$ の収束が生じても、モデル全体としての表現力を維持できます。
$$
\text{Output} = \text{LayerNorm}\left(X + \text{MultiHead}(Q, K, V)\right) \tag{4}
$$
ここで:
- $\text{MultiHead}(Q, K, V)$ は式 (2) の出力です。
- $X$ は層の入力(元の埋め込みベクトルまたは前層の出力)です。
- $\text{LayerNorm}$ は 3.3 節で説明される正規化操作で、数値の安定性を高めるために用いられます。
補足: エンコーダー部以外の Attention
Transformer ではエンコーダー部以外にも以下の 2 つの Attention があります。
-
デコーダーの Self-Attention: 未来のトークン情報を参照できないようにするため、マスク(未来位置のスコアを無効化) を適用します。この違いにより、エンコーダーは全体的な文脈を捉え、デコーダーは因果的な生成を保証します
-
エンコーダーデコーダー間の Attention: デコーダーのクエリ ($Q$) に対してエンコーダーの出力 ($K, V$) を用いることで、入力全体の文脈を参照しながら出力を生成する役割を果たします。これは Sefl-Attention ではなく Cross-Attention になります
🐣 ここも深掘りすると面白いんですが長くなるので今回は割愛…
4 なぜ Self-Attention なのか?
論文では Self-Attention を選んだ理由を3つの観点から説明しています:
- 計算量的な複雑さ
- 層あたりの総計算量
- 並列化可能な計算量(最小のシーケンシャル演算)
- ネットワーク内の最長パス(長距離依存の学習)
- 並列計算の容易さ
- Self-Attention は完全に並列化可能
- RNN は本質的に逐次処理が必要
- 長距離依存関係の学習
- Self-Attention: 全ての位置間で直接的な依存関係を学習可能
- RNN: 距離に応じて指数関数的に情報が減衰
- CNN: 受容野を広げるには多くの層が必要
これらの利点から、Self-Attention が選択されました。
補足: 結局従来の Attentionと本質的にどこが違うのか?
従来の Attention (例えば、BahdanauやLuongのモデル)では、エンコーダーとデコーダー間で Attention が機能します。この場合:
- query ($Q$) はデコーダーの隠れ状態から取得されます。
- key ($K$) と value ($V$) はエンコーダーの隠れ状態から取得され、通常は同一の表現が使用されます。
この Attention では、デコーダーの現在の状態($Q$)とエンコーダーの各隠れ状態($K$)との間でスコアを計算し、そのスコアに基づいて重み付けされたコンテキストベクトル( $V$ の加重平均)を生成します。
一方、Transformer では、 Attention 機構が大きく進化しています。主な違いは以下のとおりです:
-
Self-Attention 機構の導入:Transformerは Self-Attention を使用し、同一の入力シーケンス内での単語間の依存関係を捉えます。
-
$Q$、$K$、$V$ の独立した線形変換:
- 入力の埋め込み表現や隠れ状態に対して、独立した線形変換を適用して query ($Q$)、key ($K$)、value ($V$) を生成します。
- これにより、各単語が持つ異なる側面を別々に表現できます。
-
$K$と$V$の分離:
- key ($K$):各単語が他の単語から「注目されるべき特徴」を表現します。これは文中での関係性や役割を示します。
- value ($V$):実際に伝達すべき「内容」や「意味情報」を持ちます。
この設計により、Transformerは異なる $V$ であっても類似した $K$ を付与できる柔軟性があるわけです。
その結果として以下を利点を持ちます。
-
柔軟な関係性の捉え方:異なる品詞や概念であっても、文中で似た役割や関係性を持つ単語間の関連性を、key ($K$) を通じて効果的に捕捉できます。
-
意味情報の明確な区別:各単語の固有の意味や情報は、value ($V$) によって適切に区別・伝達されます。
-
文脈に依存する表現の理解:文脈によって意味が異なる同一表現を適切に扱えるようになりました。
つまり Transformer の最も革新的な部分の一つは「$K$-$V$分離による関係性モデリングの柔軟化」にあるといえます。
5 数値実験と結果
翻訳タスクにおける性能
WMT 2014 英独翻訳タスクにおいて、Transformer は “big” モデルで BLEU スコア 28.4 を達成し、当時の最先端モデルを超えました。また、“base” モデルは約 12 時間で学習が完了しています。
🐣 最近の BLEU スコアは 40 を軽く越しているそうです
6 まとめ
Transformer モデルは、Self-Attention を基盤にした革新的なアーキテクチャであり、従来の RNN や CNN を凌駕する性能を示しました。Attention を通じて、長距離依存を効率的に捉えながら、計算効率も向上しています。今後の研究では、さらなる効率化や他のドメインへの適用が期待されます。
🐣 そしてその後、期待を大きく上回る結果を出していくわけです
おわりに
論文の最後で示唆されているように、Transformer はその後あらゆるドメインで採用され大成功を収めました。現在、Hugging face の LLM はほぼ 100%、全体でも 90% を優に超すモデルが Transformer ベースだといわれています。一生に一本くらいはこんな論文を書いてみたいですよね。ではまた次の記事で。