AI・機械学習関連論文Advent Calendar 2024

論文紹介: AGENT SKILL ACQUISITION FOR LARGE LANGUAGE MODELS VIA CYCLEQD

Last updated at 2024-12-06Posted at 2024-12-05

はじめに

今回は、Sakan-AI の So Kuroki らによる「AGENT SKILL ACQUISITION FOR LARGE LANGUAGE MODELS VIA CYCLEQD」という論文を紹介します。この研究では、特定のタスクについて訓練された複数の大規模言語モデル (LLM) を初期個体群として、複数のタスクに適用可能な LLM を進化的に獲得する手法を提案しています。具体的には個体群内の LLM の多様性を保つために CycleQD というフレームワークを提案し、その有効性を数値実験により示しています。

参考文献:
S. Kuroki, T. Nakamura, T. Akiba, Y. Tang. "Agent Skill Acquisition for Large Language Models via CycleQD". Preprint (2024).

🐣 最近の論文で予定になかったのですが面白そうなので読んじゃいました

0 進化型計算に関する予備知識

進化型計算を理解するための基礎知識を簡潔に解説します。内容は主に遺伝的アルゴリズム（Genetic Algorithm, GA）に基づいていますが、他の進化型計算にも応用可能です。

初期収束 (Premature Convergence)

探索初期に個体群の多様性が失われ、特定の個体に収束する現象です。この現象が起きると、交叉の効果が低減し探索が停滞するため大きな問題となります。

島モデル遺伝的アルゴリズム (Island Model GA)

通常の GA では単一の個体群を使用しますが、島モデルでは個体群を複数の部分個体群 (島) に分割します。各島では独立して進化を進めつつ、特定の世代ごとに他の島にエリート個体 (最良個体) を移民として移住さる操作が実行されます。

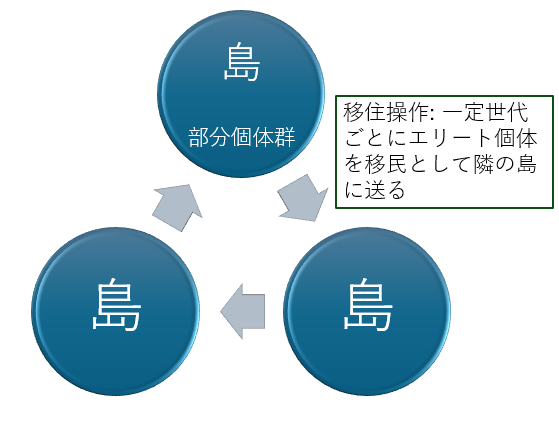
島モデル GA の概要図

論文では、島モデルに類似したアーカイブという構造を使用しており、各アーカイブは基本的に独立して進化します。

セルラー GA (Cellular GA)

2 次元格子状の空間に個体を配置し、ノイマン近傍 (上下左右) やムーア近傍 (周囲 8 近傍) を用いて遺伝演算子を適用する手法です。並列処理に適しており、個体群の多様性維持にも優れています。

セルラー GA の概要図

論文では、アーカイブ内の構造がセルラー GA に類似しています。ただし、超立方体構造を持つ点と遺伝演算子の近傍がない点が異なります。

多目的 GA (Multi-objective GA)

複数の目的関数を同時に最適化する手法です。多目的最適化では、各目的間のトレードオフが存在するため、パレート最適解を探索します。解の多様性が重要であり、論文では Q と BC を用いて類似の効果を実現しています。

世代交代モデルと連続世代モデル

従来の GA では世代交代ごとに個体群全体を更新しますが、連続世代モデルでは親から子を生成するたびに個体を逐次更新します。論文内の手法は各世代で親から 1 つだけ子を生成するので連続世代モデルに近いですが、子個体が複数のアーカイブにコピーされる可能性がある点が異なります。

1 論文の概要

この論文では、特化型の LLM から複数のタスクに適用可能な LLM を進化的に獲得する手法として CycleQD を提案しています。CycleQD は、タスク間の学習データの比率調整や複雑な目的関数設計を必要とせず、Quality Diversity (QD) フレームワークを進化型計算における各世代でサイクル的に適用することで高い性能を発揮します。

主要な結果として、CycleQD は LLAMA3-8B-INSTRUCT モデルに基づいた LLM エージェントを進化的に統合し、コード、OS 操作、およびデータベース生成タスクで GPT-3.5-TURBO に匹敵する性能を達成しています。

図 1: CycleQD による提案手法の概要図 (原論文 Figure 1 より引用)

図 1 に提案手法の概要を示します。この図のポイントを以下に示します。

二次元格子状の各格子点 (セル) に LLM が置かれる (実際は hyoercube です)
各タスクごと (図中の X, Y, Z) に独立した個体群を持つ
上記個体群を論文中ではアーカイブと呼ぶ
各世代ごとに異なるアーカイブを順番に対象として遺伝的操作を適用 (手法名 Cycle の由来?)
初期個体群として事前に学習したエキスパート LLM が配置される
上辺のタスクの性能、図 1 上部のアーカイブであれば Task Z の性能が目的関数。これを Q と呼ぶ
Q 以外の Task の性能、図 1 上部のアーカイブであれば　Task X, Y が BC となり多様性維持に利用

2 予備知識

提案手法に関係する既存手法の説明です。

進化的戦略 (Evolutionary Strategies; ES)

ES は自然淘汰に基づいた最適化アルゴリズムで、突然変異、交叉 (再結合) 、選択を用いて候補解の集団を改善します。適応度関数に基づいて進化を進め、多様性を維持することで、初期収束を避けます。この特性により、ES は単一の最適解ではなく、多様で高性能な解を生成する QD (Quality-Diversity) 最適化に適しています。

🐣 個人的にはこの論文の手法は ES ではなく島モデルベースの多目的進化型計算に見えます

MAP-Elites

QD フレームワークの中核となるアルゴリズムで、性能と多様性を同時に最適化します。

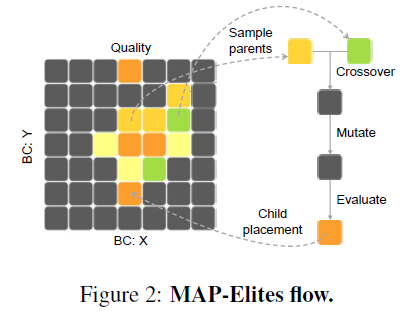
図 2: QD の中核となる MAP-Elites の流れ (原論文 Figure 2 より引用)

MAP-Elites の流れ：

アーカイブから 2 つの親を選択
後述する交叉と突然変異により子 1 つ生成
子の適応度と BC を評価
Q に相当するタスクの性能による適応度と、BC (Q 以外) のタスクの性能に基づいて既存の個体よりも優れていれば置換

これにより、性能と多様性のバランスを保ちながら解を進化させます。

3 提案手法

従来手法である MAP-Elites に比べて提案する CycleQD には以下の 3 つの特徴があります。

Quality と BC の交替: 従来手法では固定されていた Quality と Behavior Characteristics (BC) の設定を、世代ごとに動的に切り替えます。これは図 1 のように、アーカイブを 90 度回転させるような動作として捉えることができます。

🐣 論文の 90 度がわかりにくいですが『上辺が Q、それ以外が BC』という前提があるのでしょう

モデルマージを用いた交叉: 従来の手法のようにモデルパラメータを直接最適化するのではなく、モデルマージのアルゴリズムを交叉演算子として採用します。また各タスクに特化したエキスパートモデルを初期個体として使用します。
SVD ベースの突然変異: 従来のランダムな摂動ではなく、モデルパラメータ行列の主成分に沿った摂動を利用します。これにより、親モデルが形成する凸領域の外側も探索可能となります。

以下では各内容について詳述します。

3.1 Q と BC の切り替え

アーカイブの構造：

$K$ 個のタスクそれぞれが 1 つのアーカイブを管理
各アーカイブでは $K$ 個のタスクすべてに対する性能を評価 (1 つの Q、$K-1$ 個の BC)
各アーカイブは $K-1$ 次元の超立方体からなる格子状構造
Q ではないある BC タスク $k$ に対応する辺は $d_k$ 等分される。結果として格子点は $\prod_{k \neq i} d_k$ (Q 以外の区画数の積)
例えばタスク $k$ に対する各区間には、$k$ の初期エキスパートの性能の 85%〜115% を $d_k$ 分割して設定
【重要】タスク $i$ のアーカイブで新しい LLM 個体を作った場合には、このアーカイブではなく他のタスクが保持するアーカイブに対してもこの個体による置き換えを実施

補足：BC の役割

性能を 100 点満点で評価すると仮定します。例えば、ある LLM 個体の (Q のタスク性能、ある BC タスク性能) について以下の例を考えます。

LLM1：(90, 78)、LLM2：(81, 90)

このとき、Q に関しては LLM1 の 90 は LLM2 の 81 よりも高いので Q 基準であれば LLM2 を残す意味がありません。しかしながら 2 番目の BC の効果によって配置される区間が違うため競合することがありません。また、BC が 90 の区間中で LLM2 の 81 が最大の Q 性能であれば、LLM2 がその区間で生き残ることになります。いわゆる多目的最適化におけるパレート保存戦略のような効果が見込めるというわけです。

世代ごとの処理：

$t \mod K$ でアーカイブを順番に選択
選択されたアーカイブの Quality をメイン、BC をサブ的に評価して最適化
このステップで生まれた新しいモデルは全アーカイブで評価・更新を実行

親個体のサンプリング：
各アーカイブにはたくさんのパレート解が存在するため、交叉に参加する親をどう選ぶかという問題が生じます。提案手法の交叉は LLM のマージなのでコストが高く、論文では 1 世代に 1 回しか使用されていません。Q がタスク $i$ であるアーカイブ $i$ であればこのタスクの性能が高いものを選びたいところですが、生成された子は他のアーカイブでも評価されるため、BC についても考慮が必要です。そこで、その点を考慮した以下のサンプリング方が提案されています。
まず、アーカイブ $i$ 内のモデル(個体) $j$ が選択される確率 $P_j$ は次式で定義されます。

$$
P_j = \frac{\gamma_j}{\sum_{n=1}^N \gamma_n}
$$

ここで、

$N$ はアーカイブ $i$ 内のモデルの総数
$\gamma_j$ は $j$ 番目のモデルのスコア

さらに、$\gamma_j$ は次のように計算されます：

$$
\gamma_j = \prod_{i=1}^K \left( \alpha_{\text{low}} + \frac{f_{j,i} - \min(f_{1:N,i})}{\max(f_{1:N,i}) - \min(f_{1:N,i})} (\alpha_{\text{high}} - \alpha_{\text{low}}) \right)
$$

ここでの各パラメータは次の意味を持ちます：

$f_{j,i}$: $j$ 番目のモデルがタスク $i$ で達成した性能スコア。
$\min(f_{1:N,i})$, $\max(f_{1:N,i})$: タスク $i$ における全モデルのスコアの最小値と最大値
$\alpha_{\text{low}}$, $\alpha_{\text{high}}$: 正規化のためのハイパーパラメータ

補足: γ の式について

🐣 自明すぎて数学が得意な方には余計なお世話かもしれませんが…

$f_{1:N,i}$: この記号は、$1:N$ で $1$ から $N$ までの集合を表しており、「アーカイブ $i$ 内の全モデルのタスク $i$ に関する性能集合」を意味します。
論文内で $\gamma_j$ の式の直前に出てくる "the $i$-th archive..." の $i$ と $\gamma_j$ の式中の $i$ は異なる意味を持ちます。前者の $i$ は「Q が特定のタスク $i$ に対応している」という意味で、後者の $\gamma_j$ の式中の $i$ は $\prod$ の中で「(Q や BC という前提にとらわれない)全タスクにわたる変数」として使われています。この点は注意が必要です。
このことから $\gamma_j$ は Q や BC に依存する指標ではありません。そのため、アーカイブ $i$ の Q に相当するタスク $i$ の性能が極端に高くても、BC に該当するタスクの性能が低い場合は、他のモデルと比較して選ばれにくくなります。一方で、Q の性能がそこそこ高く、BC の性能が十分高いモデルは選ばれやすくなります。
この設計により、特定のアーカイブの Q のタスクに偏ることなく、全体としてパレートフロンティアの拡張を実現できます。
Q に対応するタスクを優遇する方法もありそうですが、CycleQD の設計思想に基づけば、このように全タスク間の公平性を重視した仕組みの方が適切であると判断されたようです。

3.2 モデルマージングに基づく交叉

CycleQD では、従来の遺伝的アルゴリズム (GA) のようにランダムなパラメータ交換ではなく、モデルマージングを交叉として利用します。

モデルマージングの定義

事前トレーニングされた基盤モデル $\theta_{\text{base}} \in \mathbb{R}^d$ と、特定のタスクにファインチューニングされたモデル $\theta \in \mathbb{R}^d$ の間で「タスクベクトル」$\tau$ を次のように定義します：
$$
\tau = \theta - \theta_{\text{base}}
$$

🐣 毎度おなじみ重み全体の差分ですね

このタスクベクトルは、基盤モデルから特定タスクに適応するための変更を表現します。

交叉では、親モデル $p_1$ と $p_2$ のタスクベクトル $\tau_{p_1}$ と $\tau_{p_2}$ を統合し、子モデル $\theta_{\text{child}}$ を以下のように生成します：
$$
\theta_{\text{child}} = \theta_{\text{base}} + \left( \frac{\omega_1}{\omega_1 + \omega_2} \right) \tau_{p_1} + \left( \frac{\omega_2}{\omega_1 + \omega_2} \right) \tau_{p_2}
$$
ここで、

$\omega_1, \omega_2$ は、正規分布 $\mathcal{N}(\mu, \sigma^2)$ に従って独立にサンプリングされた係数で、タスクベクトルの混合比率を決定します。
$\mu, \sigma$ は固定されたハイパーパラメータです。

🐣 要は二つのタスクベクトルの線形和を取っています

交叉の特性と安定性

多様なモデル生成:
- $\omega_1$ と $\omega_2$ をランダムにサンプリングすることで、タスクベクトルの混合比率を動的に変化させ、多様なモデルを生成します。
安定性の確保:
- $\tau_{p_1}$ と $\tau_{p_2}$ の重み係数を正規化しているため、生成された子モデルのパラメータが極端な値を取らないようにしています。

高度化の可能性

交叉については、以下のような高度化が議論されています：

親モデルの行動特性 (Behavior Characteristics, BC) に基づいて、ニューラルネットワークポリシー $\pi_\phi$ を利用して混合比率の分布パラメータ $(\mu, \sigma)$ を学習させる手法。
ただし、この手法はCycleQDの初期段階における学習負荷を増大させるため、現時点では採用されていません。

3.3 SVD に基づく突然変異

CycleQD では、モデルの能力をさらに多様化し、探索空間を拡大するために、SVD (特異値分解) に基づく突然変異を導入しています。

SVD に基づく突然変異の定義

突然変異操作は、まず交叉で得られた子モデルのタスクベクトル $\tau_{\text{child}}$ を次のように再定義します：
$$
\tau_{\text{child}} = \theta_{\text{child}} - \theta_{\text{base}}
$$

このタスクベクトル $\tau_{\text{child}}$ を層ごとの $\tau_l$ に分解し、この $\tau_l$ を SVD (特異値分解) によって次のように分解します。論文中では層ごとの重みに分解しています。
？

🐣 おそらく各層で分けないとサイズが大きすぎて特異値分解できないのかも？

$$
\tau_l = U_l \Sigma_l V_l^\top
$$

ここで、

$U_l \in \mathbb{R}^{m \times r}$: 左特異行列、
$\Sigma_l \in \mathbb{R}^{r \times r}$: 対角特異値行列、
$V_l \in \mathbb{R}^{n \times r}$: 右特異行列、
$r$: $\tau_l$ のランク (非ゼロ特異値の数) 。

突然変異の実行

SVD の結果に基づいて、次のように突然変異を適用します：
$$
\tau_l^\prime = U_l (\Sigma_l W) V_l^\top
$$
ここで、$W = \text{diag}(w_1, w_2, \dots, w_r)$ はランク $r$ に対応するスケールベクトルであり、各 $w_i$ は区間 $[0, w_{\text{max}}]$ から一様分布に従ってサンプリングされます。$w_{\text{max}}$ はハイパーパラメータとして設定されます。

最終的に、突然変異後の子モデルのパラメータは以下のように更新されます：
$$
\theta_{\text{child}}^\prime = \theta_{\text{base}} + \text{concat}({\tau_l^\prime}_l)
$$

特異値方向に基づく意味のある変動を追加することで、$\tau_{\text{child}}$ を「親モデルが形成する凸領域の外側」に拡張可能となり、新しい性能を持つモデルを探索する能力が向上します。

補足: 結局何をしたいの？

遺伝的アルゴリズムで用いられるような等方的な突然変異ではなく、モデルのパラメータ空間で「重要な方向」に沿って変化させ、新しい性能を持つモデルを効率的に探索したいということです。非常に荒っぽく説明すると、特異値分解で方向 ($V$ と $U$) とその重要度 (特異値, $\Sigma$) がわかります。そこで、特異値が小さい方向への摂動は抑えつつ、特異値が大きい方向に着眼して摂動を加えることで、モデルの特徴的な部分を強調した突然変異を実現したということです。論文中の Table 2 でガウス分布を使うよりも性能が良かったことが示されています。

4 数値実験

目的:
- CycleQD の性能を評価し、他手法 (NSGA-II, Lexicase など) と比較

🐣 NSGA-II と Lexicase はどちらも有名な多目的進化型計算手法です

実験タスク:
- マルチタスク環境でのパレートフロンティアの拡張
- タスクごとの性能をバランスよく向上させる能力を評価
主要な結果:
- パレートフロンティアの拡張:
  - CycleQD は、競合手法 (特に NSGA-II) と比較して、パレートフロンティアを広範囲に拡張
  - 各タスクの性能が偏ることなくバランス良く高い結果を示した
- Ablation Study:
  - SVD に基づく突然変異やタスク間の循環的アプローチが性能向上に重要な役割を果たすことを確認
  - 特異値方向に沿った摂動が探索効率を向上させていることが実証された
- 探索効率:
  - 少ない世代数でパレートフロンティアを大きく拡張できた
  - 他手法と比較して進化速度が速い
図表の示すポイント:
- Figure 4:
  - パレートフロンティアの拡張範囲が、従来手法と比較して広範囲に及ぶ
- Table 2:
  - 従来手法 (等方的な摂動など) よりも CycleQD が安定した高性能を達成していることを数値的に示す

CycleQD は、タスク間のバランスを保ちながら効率的に探索を進める能力が実証され、競合手法よりも優れた性能を示しました。この結果は、特異値分解に基づく突然変異や循環的最適化の有効性を裏付けています。

5 関連研究

LLM のスキル習得:
- LLM をエージェントとして活用する研究が進展 (Xi et al., 2023; Wang et al., 2024b)
- ReAct (Yao et al., 2023) のように推論と行動を統合する技術もあるが、スキル習得は従来のファインチューニングに依存し、複数スキルのバランスに課題が残る (Zeng et al., 2024; Qin et al., 2024)
**質的探索 (Quality-Diversity, QD) **:
- QD は多様かつ高性能な解を探索する進化的手法 (Pugh et al., 2016)
- MAP-Elites (Mouret & Clune, 2015) や MOQD (Pierrot et al., 2022) は、多様な行動や競合する目標に対応するために改良
- QD はニューラルネットや LLM プロンプトの探索に応用されているが、LLM の重みの進化的最適化は未開拓分野である (Guo et al., 2024; Xue et al., 2024) 。
モデルマージング:
- スパース化 (Yadav et al., 2023; Stoica et al., 2024) や最適化 (Yang et al., 2024) による進展がある

6 まとめと今後の課題

本研究の概要:
- CycleQD を提案し、従来の LLM ファインチューニングを進化的アルゴリズムで拡張
- 単一タスクのエキスパートモデルを出発点に、QD を用いて多様な特性を持つ LLM を生成
- 各タスクごとのアーカイブを設定することで多目的最適化を実現
- モデルマージングによる交叉、SVD に基づく突然変異によって LLM の進化的探索を実現
今後の研究方向:
- CMA-ME や PGA-MAP-Elites など、進化的アルゴリズムの高度な手法の適用
- CycleQD によって生成される多様なエージェントの協調や競争を通じたマルチエージェントシステムの構築

補足: 進化型計算としての視点

以下では本論文を進化型計算視点でまとめてみます。

個体群

かなり複雑な構造をしていますが、基本的にはアーカイブを部分個体群とした島モデル型であるといえます。ただし、島モデルとは違って移住はありませんが、その代わりに島モデルにはない新規生成個体による強制置換が存在します。(スーパー移住といえなくもない？)
各部分個体群は超立方体に基づく格子状空間でありセルラー GA との類似性があります。ただし、セルラー GA とは違って遺伝演算子を適用する際の近傍制約はありません。セルごとに BC の性能による区分けがあるので、地理的状況を導入したセルラー GA としてみるのが自然かもしれません。

遺伝演算子

選択が特殊で、アーカイブごとの相関を生み出しています。ただし、強力な個体が生み出された場合はアーカイブを超えて一気にその個体が広がってしまう危険性があります。
交叉の処理が重いため、1 世代で 1 個体しか生成されません。その点では連続世代モデルとの類似性が認められます。一方で、連続世代モデルとは異なり親以外とも戦えるので生き残りやすく交叉と突然変異の無駄が少ない点は探索効率的には大きな利点です。

多目的最適化

必ず Q に関する各目的関数が順番に主役になれるため中途半端なパレート解で占められてしまい探索が停滞するリスクが軽減できています。ただし、これはすべての多目的進化型計算にいえることですが、目的関数が多くなると面倒な点が顕在化しそうです。
明示的なパレート解ではなく、主となる Q と配置されるセル分けに使われる BC という分離はパレート面の多様性維持という観点からは効果的だと思われます。

拡張の可能性

格子状空間を設定しながらその近傍構造を使っていないので、交叉の選択時に反映するなどができそうです。
多様性維持の観点からはアーカイブを超えた個体のコピーは少し危険なので、同一アーカイブ内への同一個体のコピーを禁じるか既にいる同種の個体数に応じたシェアリングが適用できるかもしれません。
各アーカイブは新規個体のコピー判定時のみ相互参照するので、世代ごとに順番ではなく各アーカイブの探索を (計算資源が許すのであれば) 並列化できそうです。

おわりに

Exploration-Exploitation Trade-off をうまく解決する CycleQD フレームワークと、マージ交叉と SVD 突然変異に基づく進化的なアプローチには将来性を感じました。是非ともまた実際に動かしてみたいですね。ではまた次の記事でお会いしましょう。

🐣 CycleQBC ではないんですよね～

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up