はじめに
本記事は,以下のサイト
http://masato-ishikawa.blogspot.com/p/blog-page_13.html
にて非線形制御を初めて勉強する人向けに勧められている多様体の基礎の解説,特に冒頭の位相多様体の解説を試みたものです.
この記事が,読者の方の学習に少しでも役立ててもらえたら幸いです.
位相多様体の定義と解説の流れ
定義の紹介
解説に先立ち、位相多様体の定義を紹介します.
位相多様体の定義
位相空間$M$が次の条件を満たすとき,$M$を**$m$次元多様体(topological manifold)**という.
- $M$はハウスドルフ空間(位相空間)である.
- $M$の任意の点$p$について,$p$を含む$m$次元座標近傍$(U,\varphi)$が存在する.
定義中に
- ハウスドルフ空間(位相空間)
- 座標近傍
という言葉が出てきたので,これら2つの用語の定義も示します.
ハウスドルフ空間(位相空間)の定義
集合$X$の部分集合族$O$が次の3条件を満たすとき,$O$を$X$の**位相(toplology)と呼び,$X$と$O$の対$(X,O)$を位相空間(topologycal space)**という.
- $X\in O$ かつ $\phi\in O$
- $U_1,U_2\cdots,U_k\in O$ ならば $U_1\cap U_2\cap\cdots\cap U_k\in O$
- 任意の集合族 $(U_\lambda)_{\lambda\in \Lambda}$ について, $U_{\lambda}\in O(\forall \lambda \in \Lambda)$ ならば $\bigcup_{\lambda \in \Lambda}U_\lambda\in O$
座標近傍の定義
位相空間$X$の開集合$U$から,$m$次元数空間$R^m$のある開集合$U'$への同相写像
$$\varphi:U \rightarrow U'$$
があるとき,$U$と$\varphi$の対$(U,\varphi)$を**$m$次元座標近傍(coordinate neighbourhood)といい,
$\varphi$を$U$状の局所座標系(local coordinate system)**という.
解説の流れ
前節で紹介した定義の関係を論理記号で表すと以下の様になります.
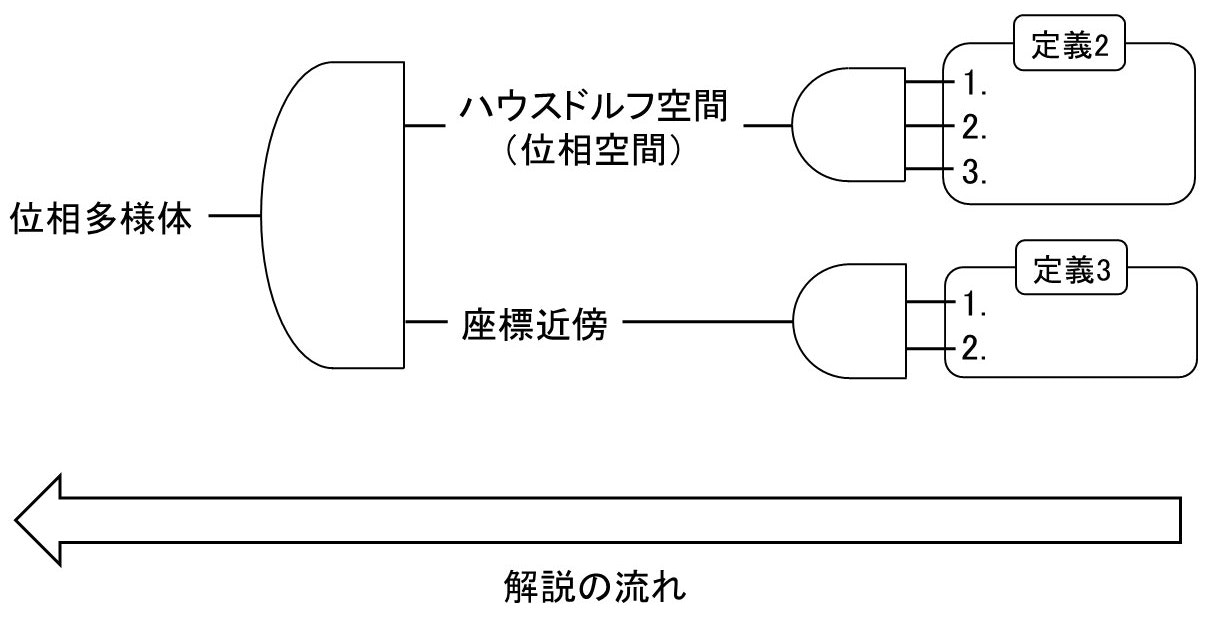
図中矢印のように,右から左にかけて定義を解説していきます.
位相多様体をなす定義の解説
「位相空間」の定義の解説
位相空間の定義を見ると,前提として
- 集合$X$
- 部分集合族$O$
- 部分集合族の$O$要素$U_i(i=1 \cdots k)$
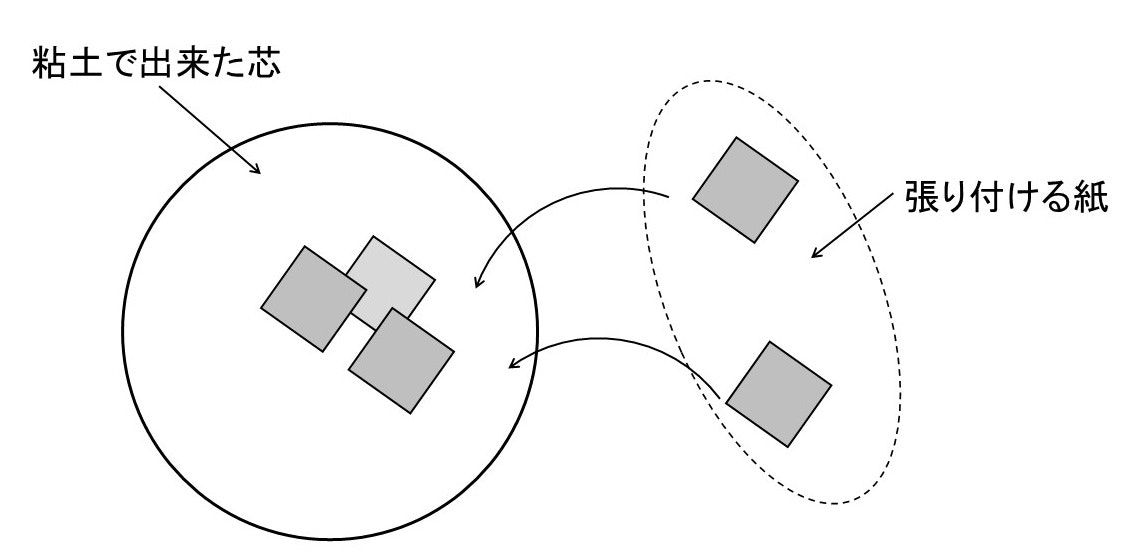
が必要だとわかるでしょう.これを張り子の球で例えると,
集合$X$ $\rightarrow$ 張り子の芯となる、球状の粘土
部分集合族$O$ $\rightarrow$ 貼り付けた紙の集まり
$O$の要素 $\rightarrow$ 貼り付けた紙一枚一枚
となります。
球が集合であるといわれて「どいうこと?」と思われる方は,3次元空間上に球の方程式を満たす点をすべてプロットしてみてください.その点全てを集合ととらえると,球とともに同じになりますよね.
これから張り子の球を例に,位相空間の定義を見てみます。
位相空間の第1の定義
1つ目の定義である,
- $X\in O$ かつ $\phi\in O$
を見てみると,まず前者の$X\in O$は,貼り付けた紙の中に1枚で球全体を覆うものがあることを意味します.
そして$\phi$は空集合を指す記号であるため,後者$\phi\in O$は,紙を貼り付けない場合も,貼り付けた紙の集まりに属しているとみなすことを意味します.
位相空間の第2の定義
次に2つ目の定義である,
2 . $U_1,U_2\cdots,U_k\in O$ ならば $U_1\cap U_2\cap\cdots\cap U_k\in O$
を見てみましょう.
定義中の$U_1,U_2\cdots,U_k$は,貼り付けた紙1枚1枚を指しており,そして$U_1\cap U_2\cap\cdots\cap U_k\in O$なので,これは貼り付けた紙の集合の中に,紙同士の共通部分とぴったり重なる紙があるということを意味します.また$\phi \in O$であるので,仮に紙を重なりなく貼り付けていても問題なくこの定義を満たします.この定義上では,$k$は有限の数を取ります.
位相空間の第3の定義
最後に3つ目の定義である,
3 . 任意の集合族 $(U_\lambda)_{\lambda\in\Lambda}$ について, $U_{\lambda}\in O(\forall \lambda \in \Lambda)$ ならば $\bigcup_{\lambda \in \Lambda}U_\lambda\in O$
を見てみます.
定義3では$\bigcup_{\lambda \in \Lambda}U_\lambda\in O$とあるように和集合記号があるので,この定義は貼り付けた紙の集合の中に,紙同士の和集合とぴったり重なる紙があるということを意味します.この定義上では,$\lambda$は有限,ないしは無限の数を取ります.
張り子の球を位相空間と呼ぶには
以上をまとめると,張り子の球を位相空間と呼ぶには,次のように紙を貼り付けなければならないことがわかります.
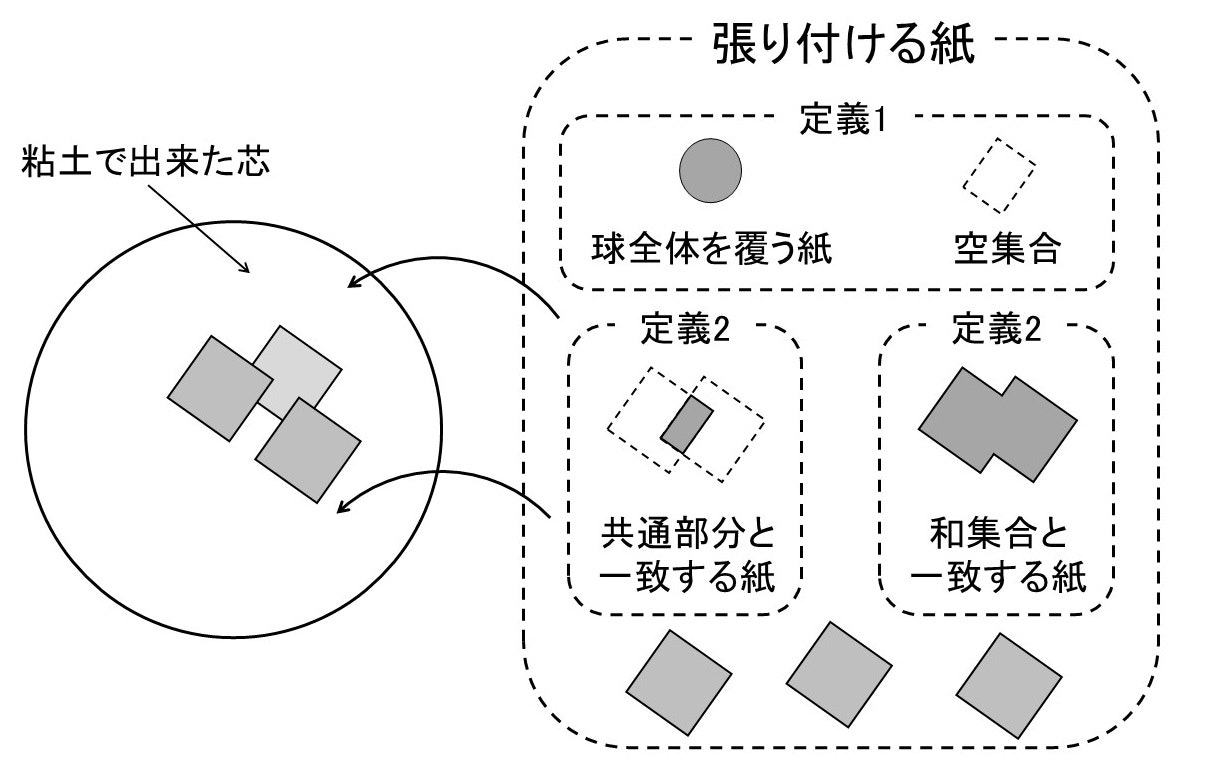
「座標近傍」の定義の解説
この定義で出てくる同相写像とは,
- 写像前と写像後が1対1で対応している($=$全単射である)
- 正写像や逆写像が連続写像である
となる写像を指します.
これを張り子の球で説明すると,下図のように貼り付けた紙からまた別の紙への写像があり,その写像が同相写像であることを意味します.
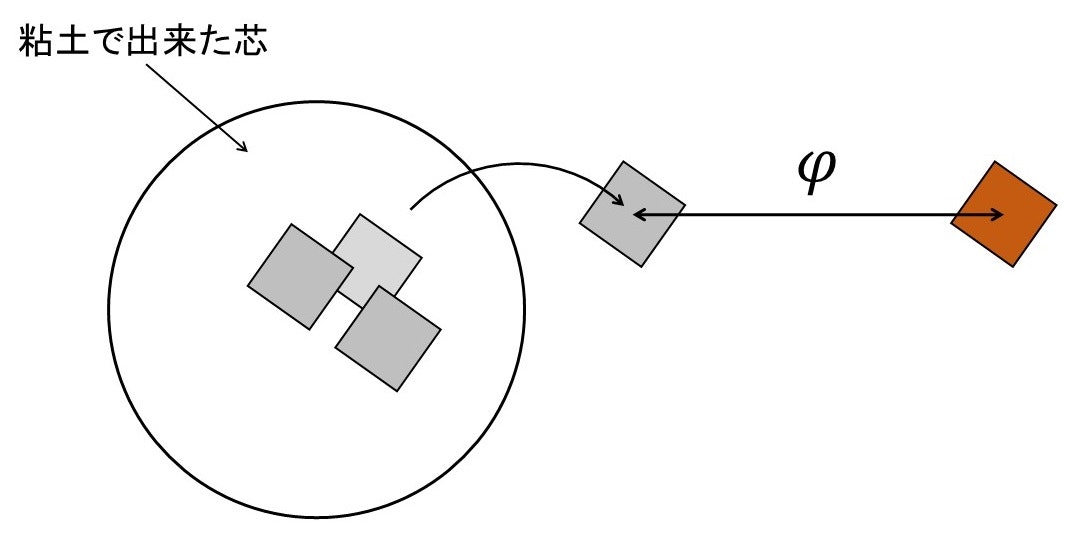
まとめ
冒頭の繰り返しになりますが,上記で解説した位相空間と座標近傍の定義を満たす空間$M$を,位相多様体と呼びます.
また,位相多様体の定義は以下のように言い換えられるのではないでしょうか.
- $M$はハウスドルフ空間(位相空間)である.
$\rightarrow$ $M$は部分空間で覆われている - $M$の任意の点$p$について,$p$を含む$m$次元座標近傍$(U,\varphi)$が存在する.
$\rightarrow$ 多様体$M$から所望の局所部分空間へ同相写像する関数が存在する.
特に2.の局所部分空間を局所座標系とすれば,位相多様体とは,好きなところに局所座標系が描けるような空間であるということを数学の言葉で表現していることになります.
番外編
位相空間とハウスドルフ空間の違い
前半の解説では,
- 位相空間
- ハウスドルフ空間
を区別しませんでしたが,厳密には違いがあります.
ハウスドルフ空間は,以下に示すハウスドルフの公理で定義されています.
ハウスドルフの公理
位相空間$(X,O)$の任意の異なる2点$p,q$に対して,$p$を含む開集合$U$と$q$を含む開集合$V$であって,互いに交わらないもの(つまり$U \cap V=\phi$)が存在する.
これを張り子の球で言うなら,貼り付けた紙の組み合わせの中で,1組でも重なり合わない組み合わせがあればハウスドルフ空間であるということができます.逆に,貼り付けた紙全てが互いに重なり合っているなら,ハウスドルフ空間とは言えないということになります.
非線形制御と微分幾何学はどう関わるのか
現代制御理論において,線形システムの
- 可制御性
- 可観測性
といった性質は(言わずもがな)非常に重要な性質であり,この記事の読者の中にも最初にこれを学んだという人も多いのではないでしょうか.(著者もそうでした)
非線形制御理論における微分幾何学の立ち位置を調査すると,上記の性質を非線形システムに拡張する試みに微分幾何学の蓄積が大いに活きているようです。
参考文献
- http://masato-ishikawa.blogspot.com/p/blog-page_13.html
- https://www.jstage.jst.go.jp/article/sicejl1962/25/11/25_11_1006/_article/-char/ja
- http://www.math.titech.ac.jp/~kawahira/courses/kiso.html
- 松本幸雄, 多様体の基礎
- Isidori, Nonlinear Control Systems third edition
更新履歴
- 2025/03/21 表記の乱れを修正