LoginSignup
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@hiyo_control(hiyo control)

線形近似と厳密な線形化の比較 ～単振子の角度レギュレーションを例に～

Last updated at Posted at 2025-08-10

はじめに

　本記事のタイトルにある「厳密な線形化」・「線形近似」はともに非線形システムを制御する方法ですが、「線形近似の方が簡単かつ、欲しい性能を得るのに十分であるため、厳密な線形化が応用される場面は少ない」というのが筆者の調べた限りの印象です。
　そこで、この印象がどれだけ正しいかを確認するため、単振子の角度レギュレーションを例に、厳密な線形化と線形近似を応用して制御器を設計し、挙動を比較することにしました。

※ 注意点
本記事では厳密な線形化を応用した制御器設計法を述べますが、理論的な説明などは省略します。
詳細を知りたい方は以下記事を参考いただけると幸いです。
http://www.sl.sc.e.titech.ac.jp/SCHPPUBLIC/lecture/iolin.pdf

例とする単振子の運動方程式

単振子の外観

　本記事では下図のように回転部に加速度が働く振子を扱います。

　この振子の運動方程式は下式です。

I\ddot{\theta}=-d_p\dot{\theta}-\frac{1}{2}mgl\sin{\theta}+\frac{1}{2}ml\cos{\theta}\ddot{x}

　式中の文字の意味を下表にまとめます。

文字 文字の意味 単位
$\theta$ 振子角度 rad
$m$ 振子質量 kg
$I$ 振子の慣性モーメント kg*m^2
$l$ 振子長さ m
$d_p$ 振子角速度に比例する粘性抵抗 N*sec/rad
$\ddot{x}$ 回転部に働く加速度 m/sec^2
$g$ 重力加速度 m/sec^2

振子の運動モデル

　次節より制御設計について述べますが、それに先立ち、運動方程式を以下のような非線形の状態方程式に変換します。

  • 状態変数
\boldsymbol{z}=
\begin{bmatrix}
  z_1\\
  z_2
\end{bmatrix}
=
\begin{bmatrix}
  \theta \\
  \dot{\theta}
\end{bmatrix}
  • 状態方程式
\begin{bmatrix}
  \dot{z_1} \\
  \dot{z_2}
\end{bmatrix}
=
\begin{bmatrix}
  z_2 \\
  -\frac{d_p}{I}z_2-\frac{mgl}{2I}\sin{z_1}
\end{bmatrix}
+
\begin{bmatrix}
  0 \\
  \frac{ml}{2I}\cos{z_1}
\end{bmatrix}
\ddot{x}

\dot{\boldsymbol{z}}=f({\boldsymbol{z}})+g({\boldsymbol{z}})\ddot{x}
  • 出力方程式
y=z_1=h(\boldsymbol{z})

制御器設計

線形近似の場合

　振子の角度$\theta =z_1$を微小とみなすと、$\sin{z_1}$と$\cos{z_1}$は以下のように見なすことができます。

\begin{align*}
    \sin{z_1} &\rightarrow z_1
    \\
    \cos{z_1} &\rightarrow 1
\end{align*}

このようにみなすと、状態方程式は以下のように線形化できます。

\begin{bmatrix}
  \dot{z_1} \\
  \dot{z_2}
\end{bmatrix}
=
\begin{bmatrix}
  0 && 1 \\
  -\frac{mgl}{2I} && -\frac{d_p}{I}
\end{bmatrix}
\begin{bmatrix}
  z_1 \\
  z_2
\end{bmatrix}
+
\begin{bmatrix}
  0 \\
  \frac{ml}{2I}
\end{bmatrix}
\ddot{x}

\dot{\boldsymbol{z}}=\boldsymbol{A}\boldsymbol{z}+\boldsymbol{b}\ddot{x}

この状態方程式に対して、下記に示す線形状態フィードバックを考えます。

\ddot{x}=
-\begin{bmatrix}
  f_1 && f_2
\end{bmatrix}
\begin{bmatrix}
  z_1\\
  z_2
\end{bmatrix}
=
-\boldsymbol{f}\boldsymbol{z}

すると、閉ループ系は、

\dot{\boldsymbol{z}}=\{\boldsymbol{A}-\boldsymbol{b}\boldsymbol{f}\}\boldsymbol{z}

となります。
この閉ループ系$\boldsymbol{A}-\boldsymbol{b}\boldsymbol{f}$の極が安定（=極の実部が負）になるように$\boldsymbol{f}$を設計すれば、振子を安定化できます。

厳密な線形化の場合

以下に示す非線形な状態方程式と出力方程式を厳密な線形化、つまり非線形項を打ち消すように制御器を設計します。

  • 状態方程式
\begin{bmatrix}
  \dot{z_1} \\
  \dot{z_2}
\end{bmatrix}
=
\begin{bmatrix}
  z_2 \\
  -\frac{d_p}{I}z_2-\frac{mgl}{2I}\sin{z_1}
\end{bmatrix}
+
\begin{bmatrix}
  0 \\
  \frac{ml}{2I}\cos{z_1}
\end{bmatrix}
\ddot{x}

\dot{\boldsymbol{z}}=f({\boldsymbol{z}})+g({\boldsymbol{z}})\ddot{x}
  • 出力方程式
y=z_1=h(\boldsymbol{z})

本記事では入力→出力を線形化する入出力線形化を応用し、制御器を設計します。
まず、入力$\ddot{x}$が陽に現れるまで出力$y=h(\boldsymbol{z})$を微分します。

  • 微分1回目
\begin{align*}
  \dot{y}
  &=\frac{\partial h(\boldsymbol{z})}{\partial \boldsymbol{z}}\dot{\boldsymbol{z}} \\
  &=\frac{\partial h(\boldsymbol{z})}{\partial \boldsymbol{z}}\{f(\boldsymbol{z})+g(\boldsymbol{z})\ddot{x}\} \\
  &=\frac{\partial h(\boldsymbol{z})}{\partial \boldsymbol{z}}f(\boldsymbol{z})
  +
  \frac{\partial h(\boldsymbol{z})}{\partial \boldsymbol{z}}g(\boldsymbol{z})\ddot{x} \\
  &=L_fh(\boldsymbol{z})+L_gh(\boldsymbol{z})
\end{align*}

この右辺第二項は、

\begin{align*}
  L_gh(\boldsymbol{z})
  &=
  \frac{\partial h(\boldsymbol{z})}{\partial \boldsymbol{z}}g(\boldsymbol{z}) \\
  &=
  \begin{bmatrix}
    1 && 0
  \end{bmatrix}
  \begin{bmatrix}
    0
    \\
    \frac{mgl}{2I}\cos{z_1}
  \end{bmatrix}
  \\
  &=0
\end{align*}

であるので、入力は陽に現れません。

  • 微分2回目
\begin{align*}
  \ddot{y}
  &=\frac{\partial L_fh(\boldsymbol{z})}{\partial \boldsymbol{z}}\dot{\boldsymbol{z}} \\
  &=\frac{\partial L_fh(\boldsymbol{z})}{\partial \boldsymbol{z}}\{f(\boldsymbol{z})
  +
  g(\boldsymbol{z})\ddot{x}\} \\
  &=\frac{\partial L_fh(\boldsymbol{z})}{\partial \boldsymbol{z}}f(\boldsymbol{z})
  +
  \frac{\partial L_fh(\boldsymbol{z})}{\partial \boldsymbol{z}}g(\boldsymbol{z})\ddot{x} \\
  &=L_f^2h(\boldsymbol{z})+L_gL_fh(\boldsymbol{z})\ddot{x}
\end{align*}

$L_fh(\boldsymbol{z})$は、

\begin{align*}
  L_fh(\boldsymbol{z})
  &=
  \frac{\partial h(\boldsymbol{z})}{\partial \boldsymbol{z}}f(\boldsymbol{z}) \\
  &=
  \begin{bmatrix}
    1 && 0
  \end{bmatrix}
  \begin{bmatrix}
    z_2 \\
    -\frac{d_p}{I}z_2-\frac{mgl}{2I}\sin{z_1}
  \end{bmatrix}
  \\
  &=z_2
\end{align*}

であるので、この右辺第二項は、

\begin{align*}
  L_gL_fh(\boldsymbol{z})&=\frac{\partial L_fh(\boldsymbol{z})}{\partial \boldsymbol{z}}g(\boldsymbol{z})\\
  &=
  \begin{bmatrix}
    0 && 1
  \end{bmatrix}
  \begin{bmatrix}
    0 \\
    \frac{mgl}{2I}\cos{z_1}
  \end{bmatrix}
  \\
  &=\frac{mgl}{2I}\cos{z_1}
\end{align*}

となります。制御入力が陽に現れたので、微分はここで止めます。

次に制御入力$\ddot{x}$の構造を

\ddot{x}=\alpha+\beta v

とし、$y$を2階微分（=制御入力が陽に現れるまで微分）した式が、

\ddot{y}=v

となるように$\alpha$と$\beta$を決定します。
これを計算すると、

\begin{align*}
  \ddot{y}
  &=L_f^2h(\boldsymbol{z})+L_gL_fh(\boldsymbol{z})(\alpha+\beta v)\\
  &=L_f^2h(\boldsymbol{z})+L_gL_fh(\boldsymbol{z})\alpha+L_gL_fh(\boldsymbol{z})\beta v \\
\end{align*}

となるので、$\alpha$と$\beta$は以下のようになります。

\alpha=-\frac{L_f^2h(\boldsymbol{z})}{L_gL_fh(\boldsymbol{z})}

\beta=\frac{1}{L_gL_fh(\boldsymbol{z})}

$\alpha$と$\beta$の分子/分母の要素は以下となります。

\begin{align*}
  L_f^2h(\boldsymbol{z})
  &=\frac{\partial L_fh(\boldsymbol{z})}{\partial \boldsymbol{z}}f(\boldsymbol{z}) \\
  &=
  \begin{bmatrix}
    0 && 1
  \end{bmatrix}
  \begin{bmatrix}
    z_2 \\
    -\frac{d_p}{I}z_2-\frac{mgl}{2I}\sin{z_1}
  \end{bmatrix}
  \\
  &=-\frac{d_p}{I}z_2-\frac{mgl}{2I}\sin{z_1}
  \\
  \\
  L_gL_fh(\boldsymbol{z})&=\frac{mgl}{2I}\cos{z_1}
\end{align*}

上記の$\alpha$と$\beta$を適用した式、

\ddot{y}=v

に対して、下記の様な線形状態フィードバックを考えます。

\begin{align*}
  v
  &=-
  \begin{bmatrix}
    k_1 && k_2
  \end{bmatrix}
  \begin{bmatrix}
    y \\ \dot{y}
  \end{bmatrix}
\end{align*}

このとき、

\begin{bmatrix}
  y \\ \dot{y}
\end{bmatrix}
=
\begin{bmatrix}
  z_1 \\ z_2
\end{bmatrix}

であるので、

\ddot{y}=v
\rightarrow
\dot{\boldsymbol{z}}
=
\begin{bmatrix}
  0 && 1 \\
  0 && 0
\end{bmatrix}
\boldsymbol{z}
-\boldsymbol{k}\boldsymbol{z}

と書くこともできます。
この閉ループ系の極が安定（=極の実部が負）になるように$\boldsymbol{k}$を設計すれば、振子を安定化できます。

線形近似と厳密な線形化の比較結果（シミュレーション）

シミュレーション条件

線形近似と厳密な線形化両者の制御器設計法を述べたので、設計法で振子の挙動に違いが出るかをシミュレーションで確認します。
シミュレーション条件は下記です。

パラメータ名 値 単位
振子質量 0.21 kg
振子長さ 0.6413 m
振子角速度に比例する粘性抵抗 0 N*sec/rad
重力加速度 9.81 m/sec^2
サンプル時間 0.01 sec
閉ループ極 -1.185±4.9346j -

振子は一様な棒とみなすので、慣性モーメントは以下で計算できます。

I=\frac{1}{3}ml^3

線形近似と厳密な線形化で閉ループ極が異なると両者の比較ができないので、表で示した極に統一します。
そのためのフィードバックゲインは以下です。

  • 線形近似
\boldsymbol{f}=
\begin{bmatrix}
  1.2007 \\
  1.0133
\end{bmatrix}^T
  • 厳密な線形化
\boldsymbol{k}=
\begin{bmatrix}
  25.7541 \\
  2.37
\end{bmatrix}^T

シミュレーション結果

振子初期角度が微小

　まずは振子の初期角度を

\theta_{initial}=20 \text{[deg]}

としたときの挙動を比較します。
　狙いは線形近似が成立する領域での振子の挙動を比較することです。
　シミュレーション結果は以下となります。

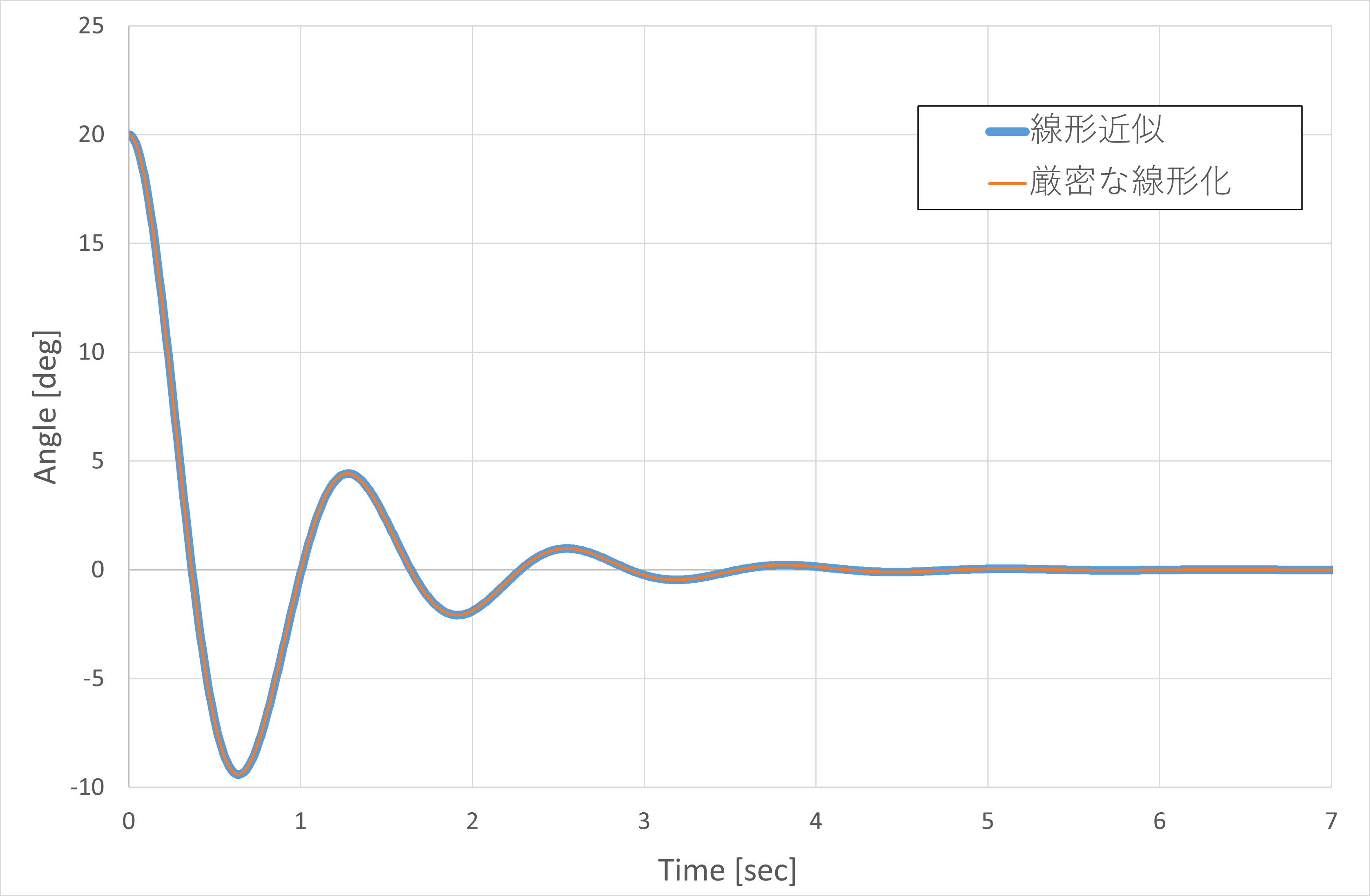
図より、

  • 両制御器ともに振子のレギュレーションが達成されていること
  • 両制御器の挙動がほぼ一致していること
    がわかります。

振子初期角度が大きい

　次に、振子の初期角度を

\theta_{initial}=200 \text{[deg]}

としたときの挙動を比較します。
　狙いは線形近似が成立しない領域での振子の挙動を比較することです。
　シミュレーション結果は以下となります。

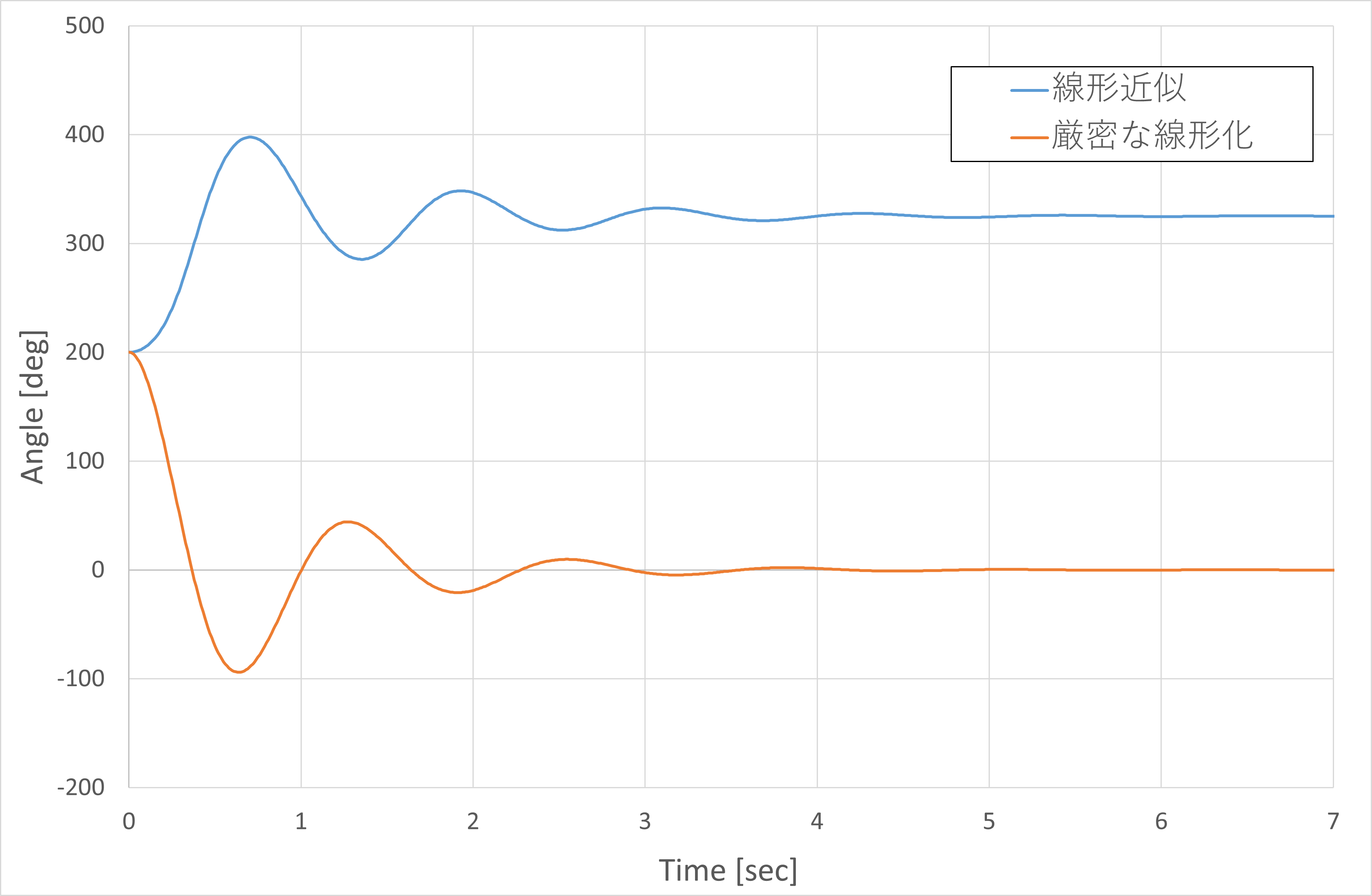
図より、線形近似が成立しない場合、線形近似で作った制御器では振子の安定化は達成できないことがわかります。

結論

　あくまで「単振子の角度レギュレーション」に限った話ではありますが、単振子の角度が小さい場合なら「線形近似でも欲しい性能を得るのに十分である」ことがわかりました。

本記事で使用したシミュレータ

本記事で使用したシミュレータは以下Githubリンクにて公開しております。

0
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?