はじめに
本記事で扱うカルマンフィルタは最もポピュラーなリアルタイム推定・ノイズ除去アルゴリズムであり,Qiitaではこのカルマンフィルタの理論・設計法に関する有益な記事が数多く投稿されています.
しかし,私の調べてた限りでは,カルマンフィルタによって実機がどれほど改善するかを述べた記事は見受けられませんでした.そこで,本記事では自作したBall&Beamを対象に,カルマンフィルタ実装前後の挙動を比較することで,カルマンフィルタによる実機挙動の改善効果を示すことを目的としました.
カルマンフィルタの概要
まずはカルマンフィルタの概要について述べますが,前述のように,カルマンフィルタの詳細については数多くの記事が投稿されているので,ここでは簡単な説明にとどめます.
カルマンフィルタの構造や,実機との関係をブロック線図にすると以下のようになります.

図のように,
- 実機からのセンサ情報とモデルによる推定値との誤差をフィードバックすること
- フィードバックゲインは統計処理に基づいて時々刻々と変わること
が,カルマンフィルタの特徴です.
自作Ball&Beam
本節で,私の作ったBall&Beamを紹介します
外観とシステム構成
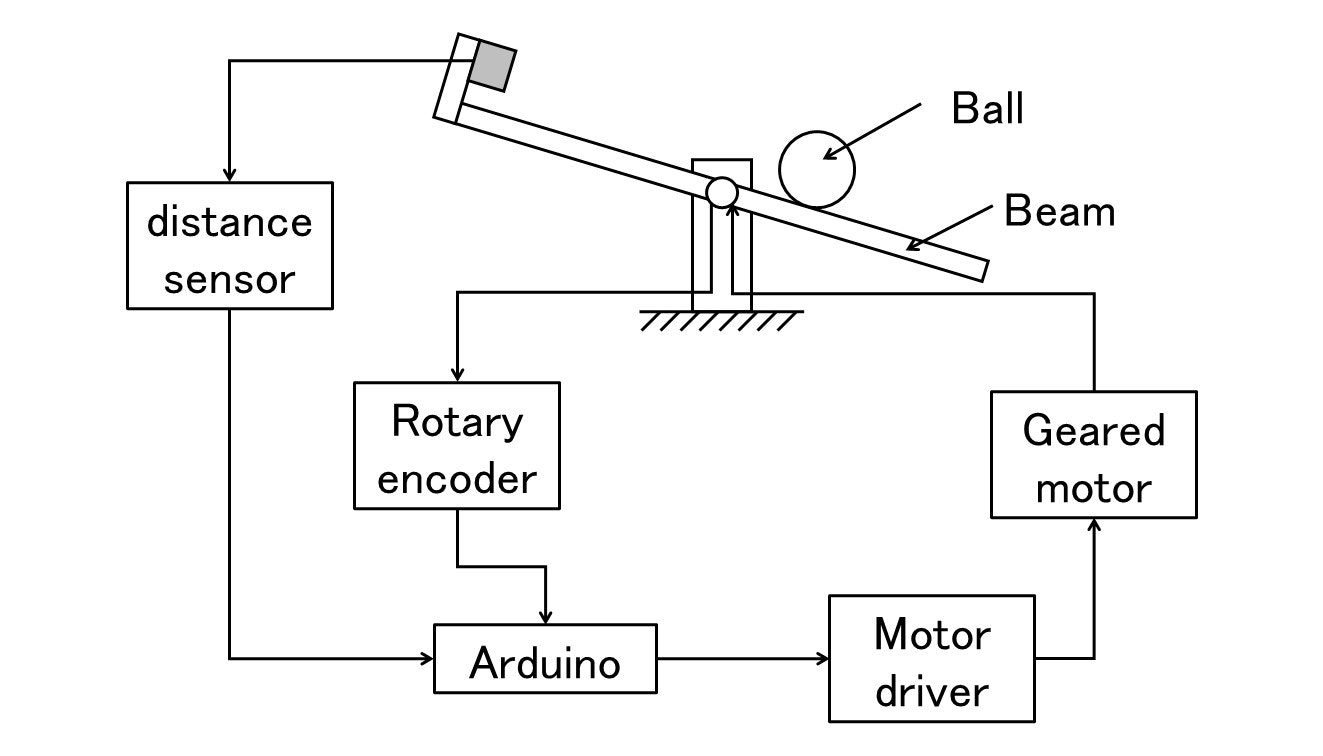
右図のように,距離センサ・ロータリエンコーダからBall位置・Beam角度情報をArduinoへ入力し,Arduinoはそれらのセンサ情報に基づき,モータドライバ・ギヤードモータからなるアクチュエータ系へ指令を送ることで,Ball位置が常にBeam回転軸にあるように制御します.
Ball&Beamの制御器構成
Arduinoに実装するBall&Beamの制御器は線形状態フィードバックに基づいて設計します.Ball&Beamの状態は
- Ball位置・速度
- Beam角度・角速度
の4つとします.Ball速度・Beam角速度はシステム構造上,直接測定することはできないので,直接測定できるBall位置・Beam角度を後退差分し,その値を代替とします.
制御器のブロック線図を以下に示します.

Ball&Beamの挙動とセンサノイズ
カルマンフィルタを用いない場合のBall&Beamの挙動を以下の動画に示します.
ご覧のように,Beamが暴れていてBallの位置が安定せず,制御がうまくいっているとは言えません.
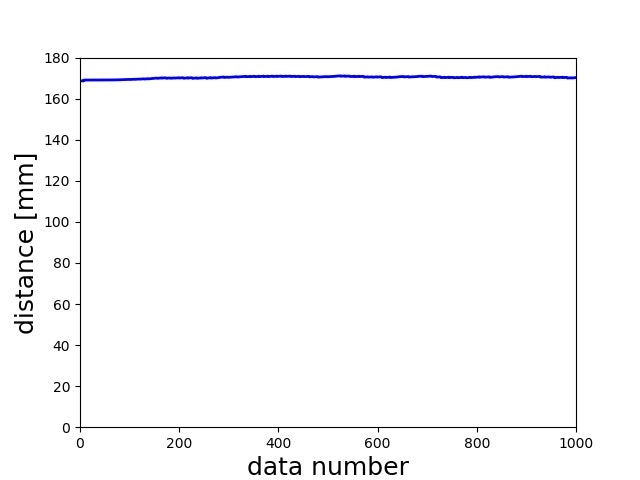
この原因究明にあたり,ひとまず高精度な計測の難しい距離センサ(シャープ測距モジュール GP2Y0A21YK)のデータを見てみました.データは下図のようにBeamを固定し,168mm先に障害物をおいて計測しました.
計測したデータの時系列波形は以下のようになります.
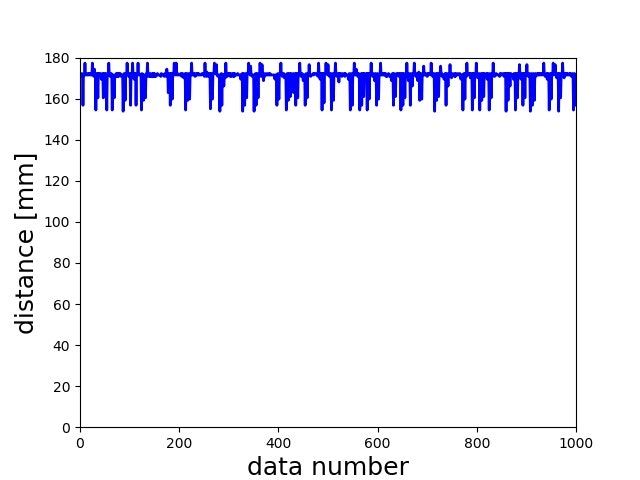
そしてこの時の分散値は
$$分散:19.1$$
です。
図や分散から,距離センサには強いノイズが含まれており,これでは制御に使えるレベルのBall距離・速度が得られないとわかります.
よって,できる限り正確なBall距離・速度を得るため,カルマンフィルタを用いることにしました.
カルマンフィルタ設計
カルマンフィルタの推定アルゴリズム
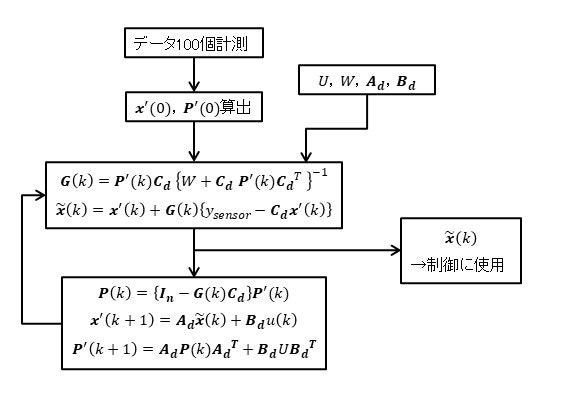
カルマンフィルタ設計にあたり,より詳細な推定フローを示します.
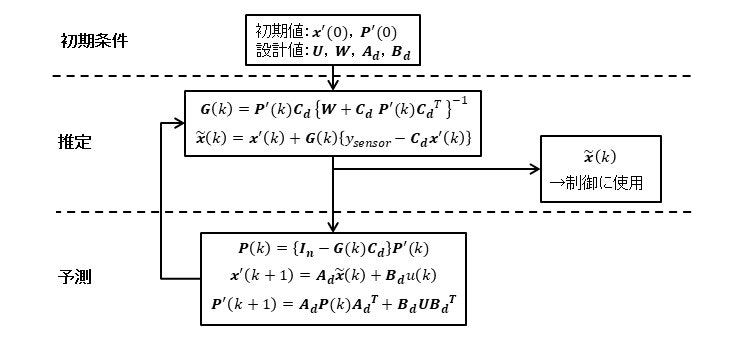
図のように,カルマンフィルタは事前情報である初期条件を受け取った後,推定→予測→推定・・・を繰り返します.
図中の文字の意味は下表のとおりです.
- 初期条件(事前情報)
| 文字 | 文字の意味 |
|---|---|
| $\boldsymbol{x'}(0)$ | カルマンフィルタの状態変数の初期値 |
| $\boldsymbol{P'}(0)$ | 状態変数の共分散行列予測値の初期値 |
| $\boldsymbol{W}$ | センサノイズの分散 |
| $\boldsymbol{U}$ | 制御入力の分散 |
| $\boldsymbol{A_d}$ | カルマンフィルタのシステム行列 |
| $\boldsymbol{B_d}$ | カルマンフィルタの入力分布ベクトル |
| $\boldsymbol{C_d}$ | カルマンフィルタの出力分布ベクトル |
- 推定
| 文字 | 文字の意味 |
|---|---|
| $\boldsymbol{G}(k)$ | カルマンフィルタのフィードバックゲイン |
| $\boldsymbol{\tilde{x}}(k)$ | 実機の状態変数の推定値 |
| $y_{sensor}$ | センサ出力 |
- 予測
| 文字 | 文字の意味 |
|---|---|
| $\boldsymbol{x'}(k)$ | カルマンフィルタの状態変数 |
| $\boldsymbol{P'}(k)$ | 状態変数の共分散行列(予測値) |
| $\boldsymbol{P}(k)$ | 状態変数の共分散行列(推定値) |
上図より,カルマンフィルタで状態推定を行うには
- 初期値:$\boldsymbol{x'}(0)$,$\boldsymbol{P'}(0)$
- 設計値:$\boldsymbol{U}$,$\boldsymbol{W}$,$\boldsymbol{A_d}$,$\boldsymbol{B_d}$
をあらかじめ決めておく必要があります.次節より,これらの事前情報について述べます.
必要な事前情報
事前情報:状態方程式と出力方程式
Ball&BeamにおけるBallの運動の様子を以下に示します.今回はカルマンフィルタでBallの位置・速度のみを推定したいので,状態方程式・出力方程式についてもBallの運動のみに注目します.

図中の文字は以下のようになります.
| 文字 | 文字の意味 |
|---|---|
| $x$ | Ball位置 |
| $m$ | Ball質量 |
| $I$ | Ball慣性モーメント |
| $r$ | Ball半径 |
| $\theta$ | Beam角度 |
| $g$ | 重力加速度 |
Ballの運動に,
- Ballは滑らないこと
- 粘性抵抗は無視すること
という仮定を置くと,運動方程式は以下のようになります.
\left(\frac{I}{r^2}+m\right)\ddot{x}=-mg\sin\theta
次にBall位置$x$とBall速度$\dot{x}$をそれぞれ状態変数$x_1$と$x_2$と置くことで,以下のような状態方程式が得られます.
\begin{bmatrix}
\dot{x_1} \\
\dot{x_2}
\end{bmatrix}
=
\begin{bmatrix}
0 & 1 \\ 0 & 0
\end{bmatrix}
\begin{bmatrix}
x_1 \\ x_2
\end{bmatrix}
+
\begin{bmatrix}
0 \\
-\frac{r^2mg}{I+mr^2}
\end{bmatrix}
\sin\theta
この状態方程式は$\theta$を入力と考えると非線形ですが,$\sin\theta$を入力とすると線形となります.よってマイコン上で$\sin\theta$の計算を行い,これをカルマンフィルタの入力とします.
Ballの状態方程式を線形で扱うことにしたので,カルマンフィルタにはシステム行列
\boldsymbol{A}=
\begin{bmatrix}
0 & 1 \\ 0 & 0
\end{bmatrix}
と入力分布ベクトル
\boldsymbol{B}=
\begin{bmatrix}
0 \\
-\frac{r^2mg}{I+mr^2}
\end{bmatrix}
を制御周期に応じて離散化した$\boldsymbol{A_d}$と$\boldsymbol{B_d}$を用いました.
次に出力方程式であるが,センサを使って距離を得るわけなので,
\begin{split}
y&=\boldsymbol{Cx} \\
&=
\begin{bmatrix}
1 & 0
\end{bmatrix}
\begin{bmatrix}
x_1 \\ x_2
\end{bmatrix}
\end{split}
となります.連続時間系と離散時間系の出力方程式は一致するため,
\begin{split}
\boldsymbol{C_d}&=\boldsymbol{C} \\
&=
\begin{bmatrix}
1 & 0
\end{bmatrix}
\end{split}
となります.
事前情報:カルマンフィルタの状態変数の初期値
Ball位置$x_1'$の初期値には,デモ前に静止状態で距離センサのデータを100個取得し,そのデータの平均値を用いることとしました.またデモ前は静止状態から始まるので,Ball速度$x_2'$の初期値はあらかじめ$0$としました.
事前情報:状態変数の共分散行列(予測値)の初期値
共分散行列
\boldsymbol{P'}
=
\begin{bmatrix}
P'_{11} & P'_{12} \\ P'_{12} & P'_{22}
\end{bmatrix}
の各要素の意味は以下の通りです.
- $P'_{11}$:Ball位置の分散
- $P'_{12}$:Ball位置とBall速度の共分散
- $P'_{22}$:Ball速度の分散
今回,Ball位置とBall速度は独立だと仮定することで,
P'_{12}=0
とします.残りの$P'{11}$と$P'{22}$は,実際にはどのような制御を行うかによるので,事前には決めづらいので,まずは,
P'_{11}=0.5 \\
P'_{22}=0.5
としました.
事前情報:センサノイズの分散
「事前情報:カルマンフィルタの状態変数の初期値」の節で述べたように,デモ前には距離センサから100個のデータを取得します.この100個のデータの分散を計算し,それをセンサノイズの分散$W$の値とします.
事前情報:制御入力の分散
カルマンフィルタにとっての入力は$\sin\theta$なので,この値の分散が$U$となります.しかしこれも$\boldsymbol{P'}$と同様に実際にはどのような制御行うかによるので,ここではひとまず
U=0.1
としました.
Ball位置・速度推定のアルゴリズム
Ball位置・速度の推定の流れを図にすると以下のようになります.
カルマンフィルタの効果検証実験
実験方法
下図のように,距離センサから168mmの距離に障害物を置きます.
そして,生データ・カルマンフィルタ推定値をそれぞれ1000個取得し,そのデータを用いて
- 測定値の時系列波形
- 平均値
- 分散
を示します.この3つの観点で,カルマンフィルタの効果を確かめます.
実験結果
まずは測定値の時系列波形を示します.左図が生データ、右図がカルマンフィルタによる推定値です。
グラフの比較から,カルマンフィルタによってノイズが抑制されていることがわかります.次に平均値・分散を表にまとめて比較してみます.
| - | 平均値 | 分散 |
|---|---|---|
| 生データ | 170.6mm | 19.1 |
| 推定値 | 170.3mm | 0.293 |
平均値はほぼ一致していますが,分散は大幅に低減されていることがわかります.
以上の結果から,カルマンフィルタにより距離センサのノイズが抑制されたことがわかります.
Ball&Beam挙動の比較
カルマンフィルタの有無でBall&Beamの虚移動がどのように変わるかを、以下の動画で示します.
カルマンフィルタの実装によって,Beamの動きが穏やかになっていることがわかります.これは,カルマンフィルタによって距離センサのノイズが抑えられたことが効いていると考えられます.
ソースコード
マイコン(Arduino)に実装したカルマンフィルタのソースコードを以下に示します.このソースコードはあくまでカルマンフィルタ用の開始プログラムであることに注意ください
- 動作前の静止状態で100個のデータ計測を許容できること
- 対象モデルが2次モデルであること
という条件を満たしていれば,本記事で扱ったBall&Beam以外でも応用することが可能です.
#include "Kalman_filter.h"
#include "Arduino.h"
Kalman_filter::Kalman_filter()
{
}
float Kalman_filter::initialization(float dist[100][1])
{
// 平均値計算-------------------------------------------------------
for (int i=0; i<100; i++)
{
dist_sum = dist[i][0] + dist_sum;
}
dist_average = dist_sum / 100;
// 分散計算---------------------------------------------------------
for (int i=0; i<100; i++)
{
dist_diff = pow(dist[i][0]-dist_average, 2) + dist_diff;
}
dist_variance = dist_diff / 100;
// 初期値設定---------------------------------------------------------
x_dash[0][0] = dist_average;
x_dash[1][0] = 0;
W = dist_variance;
return 0;
}
float Kalman_filter::Ball_estimate(float dist_sensor, float angle_sensor)
{
// calculate Kalman Gain:G(k) = P'(k)*Cd'*{ W + Cd*P'(k)*Cd' }^-1
den_G = P_dash[0][0]*pow( Cd[0][0], 2 ) + ( P_dash[0][1]+P_dash[1][0] )*Cd[0][0]*Cd[0][1] + P_dash[1][1]*pow( Cd[0][1], 2 ) + W;
G[0][0] = ( P_dash[0][0]*Cd[0][0] + P_dash[0][1]*Cd[0][1] ) / den_G;
G[1][0] = ( P_dash[1][0]*Cd[0][0] + P_dash[1][1]*Cd[0][1] ) / den_G;
// x_estimate = x_dash + G(y_sensor - y_dash)
x_estimate[0][0] = x_dash[0][0] + G[0][0]*( dist_sensor - x_dash[0][0] );
x_estimate[1][0] = x_dash[1][0] + G[1][0]*( dist_sensor - x_dash[0][0] );
// P(k) = { I-G(k)*Cd }*P'(k)
P[0][0] = P_dash[0][0]*( 1-Cd[0][0]*G[0][0] ) - P_dash[1][0]*Cd[0][1]*G[0][0];
P[0][1] = P_dash[0][1]*( 1-Cd[0][0]*G[0][0] ) - P_dash[1][1]*Cd[0][1]*G[0][0];
P[1][0] = P_dash[1][0]*( 1-Cd[0][1]*G[1][0] ) - P_dash[0][0]*Cd[0][0]*G[1][0];
P[1][1] = P_dash[1][1]*( 1-Cd[0][1]*G[1][0] ) - P_dash[0][1]*Cd[0][0]*G[1][0];
// x_dash = Ad*x_estimate + Bd*u
u = sin( angle_sensor );
x_dash[0][0] = Ad[0][0]*x_estimate[0][0] + Ad[0][1]*x_estimate[1][0] + Bd[0][0]*u;
x_dash[1][0] = Ad[1][0]*x_estimate[0][0] + Ad[1][1]*x_estimate[1][0] + Bd[1][0]*u;
// P' = APA^T + BUB^T
P_dash[0][0] = U*pow( Bd[0][0], 2 ) + Ad[0][0]*( P[0][0]*Ad[0][0]+P[1][0]*Ad[0][1] ) + Ad[0][1]*( P[0][1]*Ad[0][0]+P[1][1]*Ad[0][1] );
P_dash[0][1] = U*Bd[0][0]*Bd[1][0] + Ad[1][0]*( P[0][0]*Ad[0][0]+P[1][0]*Ad[0][1] ) + Ad[1][1]*( P[0][1]*Ad[0][0]+P[1][1]*Ad[0][1] );
P_dash[1][0] = U*Bd[0][0]*Bd[1][0] + Ad[0][0]*( P[0][0]*Ad[1][0]+P[1][0]*Ad[1][1] ) + Ad[0][1]*( P[0][1]*Ad[1][0]+P[1][1]*Ad[1][1] );
P_dash[1][1] = U*pow( Bd[1][0], 2 ) + Ad[1][0]*( P[0][0]*Ad[1][0]+P[1][0]*Ad[1][1] ) + Ad[1][1]*( P[0][1]*Ad[1][0]+P[1][1]*Ad[1][1] );
return 0;
}
float Kalman_filter::x1_kalman()
{
return x_estimate[0][0];
}
float Kalman_filter::x2_kalman()
{
return x_estimate[1][0];
}
#ifndef KALMAN_FILTER_H
#define KALMAN_FILTER_H
#include "Arduino.h"
class Kalman_filter
{
public:
Kalman_filter();
float Ball_estimate(float dist, float angle);
float initialization(float dist[100][1]);
float x1_kalman(); // Kalman filterの出力(位置)
float x2_kalman(); // Kalman filterの出力(速度)
private:
// 初期値設定変数---------------------------------------------------------------------------
float dist_sum;
float dist_diff;
float dist_average;
float dist_variance;
// kalman filter変数-----------------------------------------------------------------------
// モデル
const float Ad[2][2] = { { 1 , 0.05}, { 0 , 1 } } ; // システム行列(離散系)
const float Bd[2][1] = { {0.0074 }, {0.294 } } ; // 入力分布ベクトル(離散系)
const float Cd[1][2] = { {1 , 0 } } ; // 出力分布ベクトル(離散系,位置出力)
float x_dash[2][1]; // カルマンフィルタの状態変数
float x_estimate[2][1]; // 推定値
float u; // 制御入力
// 分散
const float U = 0.5; // 制御入力の分散
float W; // センサノイズの分散
float P_dash[2][2] = { {0.5, 0}, {0, 0.5} }; // 更新前の状態変数の分散行列(右辺は初期値)
float P[2][2]; // 更新後の状態変数の分散行列
// その他変数
float den_G; // 逆行列格納変数
float G[2][1]; // カルマンゲイン
};
#endif
参考資料
- http://www.musashinodenpa.com/arduino/ref/
- トランジスタ技術 2019年7月号
- 距離センサ:https://akizukidenshi.com/catalog/g/gI-02551/
製作に必要な部品
機械部品
| No | 品名 | 個数 |
|---|---|---|
| 1 | ロータリーエンコーダ | 1個 |
| 2 | ステンレス丸棒 150mm | 1本 |
| 3 | シャフトジョイント大 | 1個 |
| 4 | ロッドホルダ(販売中止) | 2個 |
| 5 | アングルホルダ(販売中止) | 2個 |
| 6 | ベアリング | 2個 |
| 7 | フランジ | 2個 |
| 8 | ユニバーサルアーム | 1セット |
| 9 | ユニバーサルプレート | 2セット |
| 10 | おねじめねじスペーサ(長さ45mmは販売中止) | 6本 |
| 11 | シャフトジョイント小 | 1個 |
| 12 | タミヤ ギヤボックス | 1個 |
| 13 | 絶縁スタンド | 1セット |
| 14 | DCDCコンバータ | 1個 |
| 15 | DCジャック | 1個 |
| 16 | ACアダプタ | 1個 |
| 17 | 小型ユニバーサル基板 | 1枚 |
| 18 | 距離センサ | 1個 |
| 19 | ブロックロボ | 1個 |
| 20 | ピンポン玉(100円ショップで購入できるもの) | 1個 |
電気回路部品
| No | 品名 | 個数 |
|---|---|---|
| 1 | TA7291P | 1個 |
| 2 | 3mm 白色LED | 1個 |
| 3 | 3mm 青色LED | 1個 |
| 4 | 抵抗(220Ω) | 2個 |
| 5 | 抵抗(3.3kΩ) | 2個 |
| 6 | コンデンサ(10μF) | 1個 |
| 7 | コンデンサ(220μF) | 1個 |
| 8 | コンデンサ(0.1μF) | 2個 |
| 9 | ユニバーサル基板 | 1個 |
| 10 | トグルスイッチ | 1個 |
| 11 | コネクタハウジング(2P) | 2個 |
| 12 | コネクタハウジング(3P) | 1個 |
| 13 | コネクタハウジング(4P) | 1個 |
| 14 | コネクタベース(2P) | 2個 |
| 15 | コネクタベース(3P) | 1個 |
| 16 | コネクタベース(4P) | 1個 |
| 17 | コネクタコンタクト | 20個ほど |
| 18 | ワイヤー | 1セット |
| 19 | Arduino UNO | 1個 |