Irisで前処理を試してみる。 ～標準化、無相関化、白色化～

はじめに

この記事では「はじめてのパターン認識」(通称はじぱた)の第4章4.1節のデータの前処理(線形変換)の数値例をPython(numpyのみ)で実装する。

データのロード

Scikit-kearnのload_iris()を使う。

from sklearn.preprocessing import StandardScaler
import numpy as np
from matplotlib import pyplot as plt

from sklearn.datasets import load_iris
from sklearn import preprocessing
iris = load_iris()

import pandas as pd

df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['target'] = iris.target
df.loc[df['target'] == 0, 'target'] = "setosa"
df.loc[df['target'] == 1, 'target'] = "versicolor"
df.loc[df['target'] == 2, 'target'] = "virginica"

データの中身を確認する。

df.describe()

	sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)
count	150.000000	150.000000	150.000000	150.000000
mean	5.843333	3.057333	3.758000	1.199333
std	0.828066	0.435866	1.765298	0.762238
min	4.300000	2.000000	1.000000	0.100000
25%	5.100000	2.800000	1.600000	0.300000
50%	5.800000	3.000000	4.350000	1.300000
75%	6.400000	3.300000	5.100000	1.800000
max	7.900000	4.400000	6.900000	2.500000

データの統計量を確認する。

df.cov()

	sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)
sepal length (cm)	0.685694	-0.042434	1.274315	0.516271
sepal width (cm)	-0.042434	0.189979	-0.329656	-0.121639
petal length (cm)	1.274315	-0.329656	3.116278	1.295609
petal width (cm)	0.516271	-0.121639	1.295609	0.581006

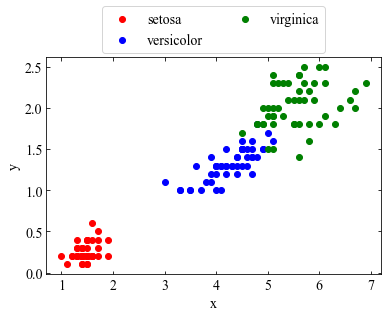
今回は「petal length」と「petal width」を対象にする。

x=df['petal length (cm)']
y=df['petal width (cm)']
z=df['target']

setosa = list(z.reset_index().query('target == "setosa"').index)
versicolor = list(z.reset_index().query('target == "versicolor"').index)
virginica = list(z.reset_index().query('target == "virginica"').index)

グラフ描画用の関数を作っておく。

def data_plot():
    plt.rcParams['font.size'] = 14
    plt.rcParams['font.family'] = 'Times New Roman'

    #目盛を内側にする。
    plt.rcParams['xtick.direction'] = 'in'
    plt.rcParams['ytick.direction'] = 'in'

    #グラフの上下左右に目盛線を付ける。
    fig = plt.figure()
    ax1 = fig.add_subplot(111)
    ax1.yaxis.set_ticks_position('both')
    ax1.xaxis.set_ticks_position('both')

    #軸のラベルを設定する。
    ax1.set_xlabel('x')
    ax1.set_ylabel('y')
    
    #元データ
    ax1.scatter(setosa_x, setosa_y, label='setosa', c='red')
    ax1.scatter(versicolor_x, versicolor_y, label='versicolor', c='blue')
    ax1.scatter(virginica_x, virginica_y, label='virginica', c='green')
    
    return ax1

ax1=data_plot()

fig.tight_layout()
ax1.legend(loc="lower center", bbox_to_anchor=(0.5, 1.02,), borderaxespad=0, ncol=2)

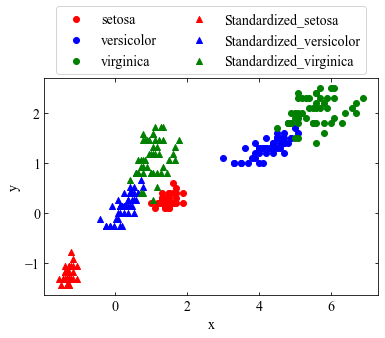
標準化

標準化とは測定単位の影響を取り除くべく、観測データの平均を0、分散を1にする変換のことである。
元のデータ$x$の平均$E\{x\}$を$\mu$、分散$Var\{x\}$を$\sigma$としたとき、線形変換
$$z=\frac{x-\mu}{\sigma}$$
を考えると、
$$E\{z\}=0、Var\{z\}=1$$
となる。
これらの関係が成り立つことを実装して確認する。

# numpyで平均、分散それぞれを計算する。
# 平均
ave_x=np.average(x)
ave_y=np.average(y)
# 分散
stdx=np.std(x)
stdy=np.std(y)

# 標準化の線形変換
nrom_x=[]
norm_y=[]
for i in range(len(x)):
    norm_x.append((x[i]-ave_x)/stdx)
    norm_y.append((y[i]-ave_y)/stdy)

#setosa, viersicolor, virginicaそれぞれをプロットするために配列を準備
setosa_x=[]
versicolor_x=[]
virginica_x=[]
setosa_y=[]
versicolor_y=[]
virginica_y=[]
n_setosa_x=[]
n_versicolor_x=[]
n_virginica_x=[]
n_setosa_y=[]
n_versicolor_y=[]
n_virginica_y=[]

for i in setosa:
    setosa_x.append(x[i])
    setosa_y.append(y[i])
    n_setosa_x.append(norm_x[i])
    n_setosa_y.append(norm_y[i])

for i in versicolor:
    versicolor_x.append(x[i])
    versicolor_y.append(y[i])
    n_versicolor_x.append(norm_x[i])
    n_versicolor_y.append(norm_y[i])

for i in virginica:
    virginica_x.append(x[i])
    virginica_y.append(y[i])
    n_virginica_x.append(norm_x[i])
    n_virginica_y.append(norm_y[i])

【参考】Scikit-learnを使う場合

# x,yを結合
data = np.c_[x, y]                                          

# 標準化を行う
sc = StandardScaler()
std = sc.fit_transform(data)

グラフを描画する。

ax1=data_plot()

ax1.scatter(n_setosa_x, n_setosa_y, label='Standardized_setosa', marker='^', c='red')
ax1.scatter(n_versicolor_x, n_versicolor_y, label='Standardized_versicolor', marker='^', c='blue')
ax1.scatter(n_virginica_x, n_virginica_y, label='Standardized_virginica', marker='^', c='green')

fig.tight_layout()
ax1.legend(loc="lower center", bbox_to_anchor=(0.5, 1.02,), borderaxespad=0, ncol=2)

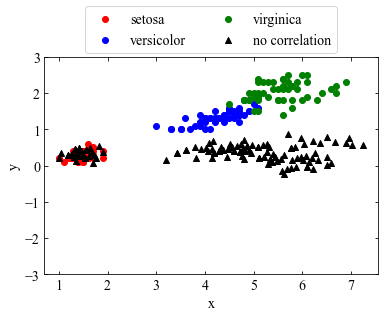
無相関化

無相関化とは、観測データ間の相関をなくす処理のことである。観測データから得られた共分散行列$\Sigma$の固有値問題
$$\Sigma \boldsymbol{s}=\lambda \boldsymbol{s}$$
を解いて得られた固有値を$\lambda_{1} \geqq \lambda_{2} \geqq \cdot\cdot\cdot\geqq\lambda_{d} $、
対応する固有ベクトルを$\boldsymbol{s_{1}, s_{2}, \cdot\cdot\cdot, s_{d}}$として、行列$\boldsymbol{S}$を以下で定義する。

$$\boldsymbol{S}=(\boldsymbol{s_{1}, s_{2}, \cdot\cdot\cdot, s_{d}})$$

観測データ$\boldsymbol{x}$に対して$\boldsymbol{S}^{T}$で線形変換を行う。すなわち、$\boldsymbol{y}=\boldsymbol{S}^{T}\boldsymbol{x}$を考えたとき、以下が成り立つ。
$$E\{\boldsymbol{y}\}=\boldsymbol{S}^{T}\boldsymbol{\mu}, Var\{\boldsymbol{y}\}=\boldsymbol{S}^{-1} \boldsymbol{\Sigma}\boldsymbol{S}=\boldsymbol{\Lambda}$$

$\boldsymbol{S}^{-1} \boldsymbol{\Sigma}\boldsymbol{S}$は$\boldsymbol{\Sigma}$の対角化そのものであるため、対角成分以外は0となる。すなわち、共分散は0となり、相関係数の定義から相関係数は0となることがわかる。

# 分散共分散行列の回転行列Sを求める。
_, S = np.linalg.eig(cov)           
S[:,1]=S[:,1]*(-1)

$\boldsymbol{S}^{T}=$$\boldsymbol{S}^{-1}$が成り立つ。すなわち、$S^{T}$$S$が単位行列であることが確認できる。

np.dot(S.T, S)

[[ 1.00000000e+00, -2.53792738e-17],
   [-2.53792738e-17,  1.00000000e+00]]

# データを無相関化 ※.Tは転置を表す
pledged_decorr = np.dot(S.T, data.T).T

$\Lambda = \boldsymbol{S}^{-1} \boldsymbol{\Sigma}\boldsymbol{S}$を求める。

lam = np.dot(np.dot(np.linalg.inv(S), cov), S)

はじぱたp.43の式(4.16)と同じ値であることを確認する。

print(lam)

[[3.66123805e+00 2.31134308e-16]
 [1.20962250e-16 3.60460707e-02]]

相関係数が0であることを確認する。

print('相関係数: {:.3f}'.format(np.corrcoef(pledged_decorr[:, 0], pledged_decorr[:, 1])[0,1]))

相関係数: 0.000

グラフを描画する。

ax1=data_plot()

ax1.scatter(pledged_decorr[:, 0], pledged_decorr[:, 1], label='no correlation', marker='^', c='black')

plt.ylim(-3,3)

fig.tight_layout()
ax1.legend(loc="lower center", bbox_to_anchor=(0.5, 1.02,), borderaxespad=0, ncol=2)

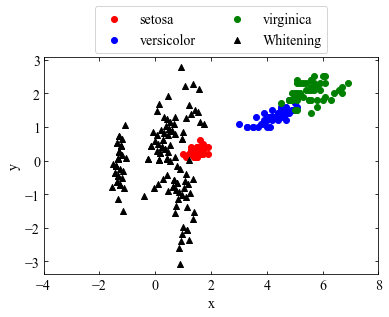
白色化

前述の$\boldsymbol{\Lambda}、\boldsymbol{S}^{T}$、観測データ$\boldsymbol{x}$の平均$\boldsymbol{\mu}$を用いて、線形変換$\boldsymbol{u}=\boldsymbol{\Lambda}^{-\frac{1}{2}}\boldsymbol{S}^{T}(\boldsymbol{x}-\boldsymbol{u})$を考えると、以下が成り立つ。
$$E\{\boldsymbol{u}\}=0$$
$$Var\{\boldsymbol{u}\}=\boldsymbol{\Lambda}^{-\frac{1}{2}}\boldsymbol{S}^{-1}\boldsymbol{\Sigma}\boldsymbol{S}\boldsymbol{\Lambda}^{-\frac{T}{2}}
=\boldsymbol{\Lambda}^{-\frac{1}{2}}\boldsymbol{\Lambda}\boldsymbol{\Lambda}^{\frac{1}{2}}=\boldsymbol{I}$$
ただし、$\boldsymbol{\Lambda}^{-\frac{T}{2}}$は$\boldsymbol{\Lambda}^{-\frac{1}{2}}$の転置行列である。このように観測データの標準偏差を1に正規化し、かつ中心化する変換を白色化と呼ぶ。

データを白色化する。

ave=np.c_[ave_x, ave_y]
lam_1_2=np.linalg.inv(np.sqrt(lam))
u = np.dot(lam_1_2, np.dot(S.T, (df_corr-ave).T))

グラフを描画する。

ax1=data_plot()
plt.xlim(-4,8)

ax1.scatter(u.T[:, 0], u.T[:, 1], label='Whitening', marker='^', c='black')

fig.tight_layout()
ax1.legend(loc="lower center", bbox_to_anchor=(0.5, 1.02,), borderaxespad=0, ncol=2)

最後に白色化後のデータの共分散行列が単位行列になっていることを確認する。

np.cov(u)

確かに単位行列になっている。

array([[ 1.00000000e+00, -6.58744352e-08],
       [-6.58744352e-08,  1.00000000e+00]])