原典
BROKEN NEURAL SCALING LAWS
https://arxiv.org/pdf/2210.14891
Published as a conference paper at ICLR 2023
有名な下記論文のスケーリング則の改善版です
Scaling Laws for Neural Language Models
https://arxiv.org/pdf/2001.08361
概要
この論文は、深層ニューラルネットワーク(DNN)の性能が、計算資源、モデルパラメータ数、データセットサイズなどの「スケール」の増大に伴ってどのように変化するか(スケーリング挙動)を予測するための新しい関数形式「Broken Neural Scaling Law (BNSL)」を提案しています。従来の単純なPower Law(べき乗則)では捉えきれなかった、性能が一時的に低下する「Double Descent」現象や、特定のスケールで急激に性能が向上する「相転移」のような複雑な挙動も、BNSLを用いることで正確にモデル化し、将来の性能をより高い精度で外挿(予測)できることを、多様なタスクと設定における広範な実験を通じて示しています。
Abstract (要旨)
- 本論文では、「Broken Neural Scaling Law (BNSL)」という新しい関数形式を提案します。
- BNSLは、DNNの評価指標(精度、損失など)が、訓練/推論に使われる計算資源、モデルパラメータ数、データセットサイズ、訓練ステップ数、上流タスクの性能などに応じてどのように変化するかをモデル化し、外挿(予測)します。
- 画像、言語、音声、動画、拡散モデル、強化学習など、非常に多様な上流・下流タスク(Zero-shot, Prompted, Fine-tuned設定を含む)において、BNSLが従来の関数形式よりも著しく高い精度でスケーリング挙動を予測できることを示します。
- 特に、Double Descentのような非単調な挙動や、算術タスクに見られるような急峻な変曲点(遅延して急激に性能が向上する点)など、他の関数形式では表現できない挙動も正確にモデル化・外挿できることを強調しています。
- 最後に、この関数形式を用いてスケーリング挙動の予測可能性の限界についても考察しています。
1 Introduction (はじめに)
- DNNの性能向上には計算資源、パラメータ数、データセットサイズの増加が不可欠であり、今後もこの傾向は続くと予想されます。
- しかし、将来の大規模なリソース環境でどの手法が最適かは現時点では不明であり、小規模での性能が大規模での性能を保証しないことが経験的に知られています。
- したがって、将来有望な手法を見極めるためには、性能がスケールに応じてどのように変化するかを予測する「ニューラルスケーリング則 (Neural Scaling Laws)」が重要になります。
- 既存のスケーリング則研究(主にPower Law)は、上流タスクの損失低下などを予測する上である程度成功しましたが、下流タスクの性能や、変曲点、非単調な挙動(例:Double Descent)といった複雑な現象を捉えるには限界がありました。
- AIの安全性(AI Safety)の観点からも、大規模化に伴う予期せぬ能力(Emergent Abilities)の発現を予測することは極めて重要です。
- 本研究は、これらの課題に対応するため、より表現力が高く、広範な現象を捉えられる新しいスケーリング則の関数形式(BNSL)を提案することを目的としています。
2 The Functional Form of Broken Neural Scaling Laws (BNSLの関数形式)
- 提案手法であるBNSLの数学的な関数形式(式1)を提示します。

- この関数は、対数-対数プロット上で、複数の滑らかに接続された区分的な(ほぼ)線形セグメントで構成されます。これは「滑らかに壊れたべき乗則」と表現できます。
-
nは「ブレーク(折れ曲がり)」の数を表し、全体でn+1個の線形セグメントが存在します。 - 各パラメータの意味を解説しています。
-
a: スケール無限大での性能の極限値(例:最小エラー)。 -
b: 対数-対数プロット上でのオフセット。 -
c0: 最初の線形セグメントの傾き。 -
ci:i番目のブレークにおける傾きの変化量。 -
di:i番目のブレークが発生するスケール(x軸上の位置)。 -
fi:i番目のブレークの鋭さ(値が小さいほど急峻な変化)。
-
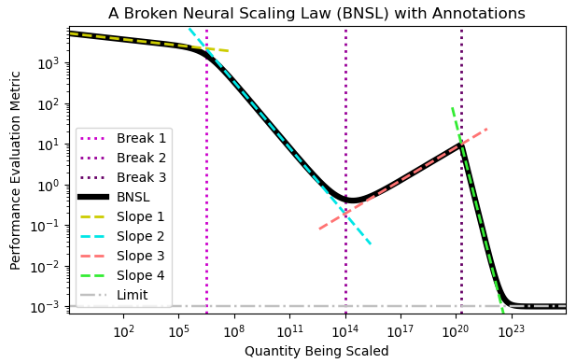
- Figure 1で、3つのブレークを持つBNSLの例を図示しています。
- この関数形式は十分なセグメントがあれば任意の滑らかな関数を近似できますが、未知の領域への外挿性能が良いかは自明ではない、としています。
3 Related Work (関連研究)
- 過去のニューラルスケーリング則に関する研究を紹介しています。
- Cortesら(1994)による初期の研究(データサイズに対する性能)。
- Hestnessら(2017)による多くの桁にわたるPower Lawの検証。
- Rosenfeldら(2019)によるモデルサイズに対するPower Law。
- Kaplanら(2020)による計算資源に対するPower Law(広く知られるきっかけ)。
- Abnarら(2021)による上流性能と下流性能の関係へのPower Law適用。
- Zhaiら(2021), Bansalら(2022)による、ランダム性能からの改善開始点を考慮した関数形式(M3)。
- Alabdulmohsinら(2022)による、データの不可削減エントロピーなどを考慮した別の関数形式(M4)とベンチマークデータセットの提供。
- Hernandezら(2021)が、特定の文脈(転移学習)でBNSLのn=1の場合と等価な形式に言及したが、一般化や検証は行われなかった点を指摘しています。
- BNSLと同様の「Broken Power Law」が天体物理学の分野で広く使われていることにも触れ、着想元の一つであることを示唆しています。
4 Theoretical Limitations of Previously Proposed Scaling Laws (既存スケーリング則の理論的限界)
- 既存のスケーリング則で提案された関数形式(M1, M2, M3, M4と呼称)の理論的な限界を数学的に分析しています。
- 単調性: M1, M2, M3 は常に単調(増加または減少の一方)であり、導関数が符号を変えないため、Double Descentのような非単調な現象を原理的に表現できません。
- 変曲点: M1, M2, M3 は(線形-線形プロット上で)変曲点を持つことができません(二階導関数が0にならないため)。多くの実データで見られる変曲点を捉えられません。
- M4の限界: M4は変曲点を表現できますが、逆関数の形で定義されているため、決定論的に単一のxに対して単一のyしか出力できず、非単調な挙動は表現できません。
- これに対し、BNSLはこれらの理論的限界を持たず、非単調性や変曲点を表現できる能力があることを示唆しています。
5 Empirical Results: Fits & Extrapolations of Functional Forms (実験結果:適合と外挿)
- BNSLが、既存の関数形式(M1-M4)と比較して、様々なタスクのスケーリング挙動をどの程度正確にモデル化し、外挿(予測)できるかを広範な実験で評価しています。
5.1 Vision (画像)
- Alabdulmohsinらのベンチマークデータセットを用い、画像分類タスクにおける上流データセットサイズに対する下流性能のスケーリングを評価。Table 2, 3でBNSLが約69%のタスクで最も良い外挿精度を示した(次点はM4の約14%)ことを報告。
- Appendixでは、計算資源に対するスケーリング、拡散モデル、動画生成モデル、ロボティクス、継続学習、敵対的頑健性、公平性など、さらに多様な画像関連タスクでのBNSLの有効性を示しています。
5.2 Language (言語)
- 同様にAlabdulmohsinらのベンチマーク(BIG-Bench, 上流LM/NMTタスク)を用い、言語タスクでのスケーリングを評価。Table 2, 4でBNSLが75%のタスクで最も良い外挿精度を示した(次点はM2, M3の10%)ことを報告。
- Appendixでは、モデルパラメータ数に対するスケーリング(Figure 2)、Sparseモデル、Retrieval拡張モデル、入力長スケーリング、RNN、音声認識、不確実性推定、分子タスク、OOD検出、量子化、蒸留、数学問題、コード生成など、極めて広範な言語・系列関連タスクでのBNSLの有効性を示しています。
5.3 Reinforcement Learning (強化学習)
- AlphaZero(コネクトフォー)、PPG(Procgen StarPilot)、PPO(Procgen Heist)といった強化学習アルゴリズムのスケーリング挙動(計算資源、データセットサイズ、パラメータ数に対して)もBNSLが正確にモデル化・外挿できることをFigure 3で示しています。
- Appendixでは、テスト時の推論計算量に対するスケーリングや、RLHF(人間からのフィードバックによる強化学習、AIアライメント)による性能向上のスケーリングについてもBNSLの有効性を示しています。
5.4 Non-monotonic Scaling (非単調スケーリング)
- BNSLが、既存手法では不可能なDouble Descent現象(モデル幅、データセットサイズに対して)を正確に捉え、外挿できることをFigure 4で実証しています。
5.5 Inflection Points (変曲点)
- BNSLが、算術タスク(4桁加算)における訓練データサイズに対する性能の急峻な変化(線形-線形プロット上の変曲点)を正確に捉え、外挿できることをFigure 5で示しています。他の関数形式ではこの変曲点を表現できません。
6 The Limit of the Predictability of Scaling Behavior (スケーリング挙動の予測可能性の限界)
- BNSLを用いても、スケーリング挙動の予測には限界があることを議論しています。
- 特に、「創発(Emergent)」「相転移(Phase Transition)」と呼ばれるような急峻な性能変化(BNSLにおける
fiが小さく|ci|が大きいブレーク)を外挿予測するには、その変化点(ブレークポイントdi)付近、あるいはそれ以降のデータ点が必要になる場合があることを指摘しています。 - 4桁加算の例では、ブレークポイント(約415)より前のデータだけでは、たとえノイズがなくても(シミュレーション結果)、正確な外挿は困難であったことを示しています。
- これは、将来現れるかもしれない未知の急峻な性能変化(新しい能力の獲得など)を、それが発生する前に完全に予測することの難しさを示唆しています。
7 Discussion (考察)
- 本研究で提案したBNSLが、非常に広範なDNNアーキテクチャ、タスク、設定におけるスケーリング挙動を正確にモデル化し、外挿できる強力な関数形式であることを改めて強調しています。
- 既存のスケーリング則の限界を克服し、Double Descentや急峻な変曲点といった複雑な現象も捉えられる点が重要な貢献です。
- 一方で、急峻な変化点の予測には限界があることも示し、今後の研究の方向性を示唆しています。
Ethics Statement (倫理的考察)
- BNSLはAIの能力向上予測に役立つ可能性がある一方、AIの安全性研究(予期せぬ能力発現の予測や、アライメント手法のスケーリング予測など)にも貢献しうると主張しています。
- BNSLの利用には十分なデータ収集が必要な場合があり、計算資源を持つ組織がより正確な予測を行えるようになることで、組織間の格差が拡大する可能性も指摘しています。
Acknowledgments (謝辞)
- 研究協力者やフィードバックを提供してくれた人々への感謝を述べています。
Appendix (付録)
- BNSLが対数-対数プロット上で区分的線形になる理由の数学的説明。
- BNSLを構成するPower Lawセグメントへの分解。
- 評価指標(RMSLE, Root Standard Log Error)の定義。
- 実験の詳細設定(4桁加算タスクのハイパーパラメータなど)。
- BNSLのフィッティング方法とブレーク数の決定方法。
- 本文で触れられた多数の追加実験結果のプロット(全36図)。
用語集
- Broken Neural Scaling Law (BNSL): 本論文で提案された、DNNのスケーリング挙動をモデル化・外挿するための新しい関数形式。対数-対数プロット上で、滑らかに接続された複数の区分的な(ほぼ)線形セグメント(べき法則)から構成される。
- Scaling Law (スケーリング則): DNNの性能や特性が、計算資源、モデルサイズ、データ量などの「スケール」の変化に伴って、どのように変化するかを記述する法則(多くは数学的関数)。
-
Power Law (べき乗則): スケーリング則の最も一般的な形式の一つ。
y = a * x^b + cのような形で表され、対数-対数プロット上で直線になる。 - Extrapolation (外挿): 観測されたデータ範囲の外側にある未知の値を、観測データに基づいて予測すること。スケーリング則の文脈では、小規模な実験結果から大規模モデルの性能を予測することを指す。
- Upstream Task (上流タスク): 大規模データを用いて事前学習されるタスク(例:言語モデリング、画像分類事前学習)。
- Downstream Task (下流タスク): 上流タスクで学習されたモデルを、特定の応用タスク(例:質問応答、物体検出、感情分析)に適応(Fine-tuningなど)させて評価するタスク。
- Zero-shot: モデルが特定のタスクの訓練データを全く見ずに、そのタスクを実行する能力。
- Prompted: 大規模言語モデルなどに対して、タスクを指示するテキスト(プロンプト)を与えることで、特定のタスクを実行させる評価方法。Few-shot Promptingは少数の例をプロンプトに含める。
- Fine-tuned: 事前学習済みモデルを、特定の(比較的小規模な)下流タスクのデータセットで追加学習させること。
- Compute (計算資源): モデルの訓練や推論に使用される計算量。多くの場合、FLOPs (Floating Point Operations) で測定される。
- Parameters (パラメータ): ニューラルネットワーク内の学習可能な重みやバイアスの数。モデルのサイズを表す指標の一つ。
- Dataset Size (データセットサイズ): 訓練に使用されるデータの量(例:サンプル数、トークン数、画像数)。
- Double Descent (ダブルディセント): モデルサイズや訓練データ量を増やしていくと、テストエラーが一度悪化してから再び改善するという、従来の統計学習理論の予測に反する現象。
- Inflection Point (変曲点): 関数のグラフで、曲がり方の向きが変わる点(凹から凸へ、または凸から凹へ)。線形-線形プロット上で、スケーリング挙動が急激に変化する(例:性能が急向上し始める)点として現れることがある。
- Grokking: DNNが訓練データに完全に過適合した後、時間をかけて汎化性能を獲得していく現象。特定のタスク(例:モジュラー算術)で顕著に見られる。これも急峻な性能変化の一種。
- Emergent Abilities / Phase Transitions / Breakthrough Behavior (創発的能力 / 相転移 / ブレークスルー挙動): モデルのスケールがある閾値を超えると、予測不能な形で急激に新しい能力が現れたり、性能が劇的に向上したりする現象を指す言葉。本論文では、BNSLにおける急峻なブレークとして捉えられる。
- Root Mean Squared Log Error (RMSLE): 予測値と真の値の対数の差の二乗平均平方根。スケーリング則の評価において、値のスケールが大きく異なる場合や、相対的な誤差を重視する場合によく用いられる誤差指標。
- Pareto Optimal (パレート最適): ある目的(例:性能)を改善しようとすると、他の目的(例:計算資源)を悪化させなければならない状態。計算資源と性能の関係において、特定の性能を達成するための最小計算資源(または特定の計算資源で達成できる最高性能)を結んだ曲線(パレートフロンティア)上でスケーリングを評価することがある。
- AI Alignment (AIアライメント): AIシステムの目標や行動を、人間の意図や価値観と一致させることに関する研究分野。
- Reinforcement Learning from Human Feedback (RLHF): 人間によるフィードバック(例:どちらの出力が良いかの比較)を報酬シグナルとして利用し、強化学習によってAIモデル(特に言語モデル)を人間の意図に沿うように訓練する手法。