統計学入門メモ(第2章_vol2_ヒストグラム操作)
やったこと
- ヒストグラムの色を変える(もうggplot2使った方がいいような・・)
- 度数分布表データを算出する
- 累積度数グラフを書く
- ローレンツ曲線を書く
ざっと読んでキーワード収集
- 階級値、相対度数、累積度数、累積相対度数、双峰型、単峰型、層別、歪んだ分布(感覚とは逆に歪むので注意)
- スタージェスの公式(目安となる階級数を求める)
$$ k = \frac{(log_{10}n)}{log_{10}2} $$
使ったデータ
R標準のdata()で出てきたサンプルデータを利用しました
LinkDataも良いんですが、地図データが多い印象で今回の記事での応用方法が分からず・・・。
leafletで使うと多分超楽しい
Rで実施
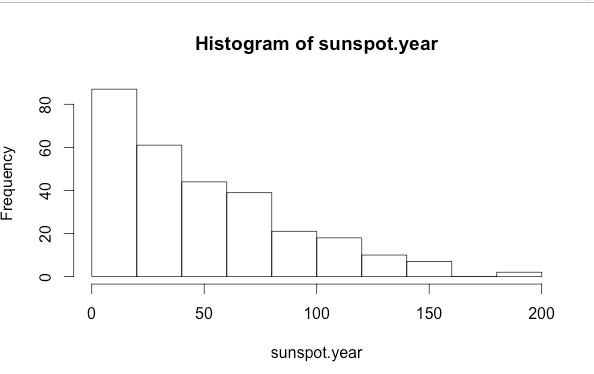
普通にヒストグラムを書く
hist(sunspot.year)
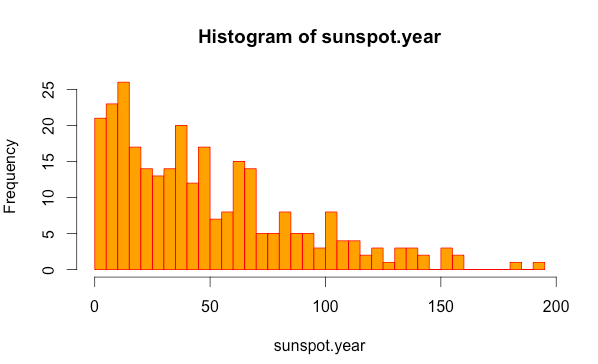
もうちょっと細かく見たり、色をつけてみたい。
hist(sunspot.year,breaks=50, col = "orange", border="red")
階級数、階級値、度数、相対度数、累積度数、累積相対度数を求める
参考ページより、hist(データ,plot=F)とすると、
度数分布表のデータが得られる。
hist(sunspot.year,plot=F)
$breaks
[1] 0 20 40 60 80 100 120 140 160 180 200
$counts
[1] 87 61 44 39 21 18 10 7 0 2
$density
[1] 0.0150519031 0.0105536332 0.0076124567 0.0067474048 0.0036332180 0.0031141869 0.0017301038
[8] 0.0012110727 0.0000000000 0.0003460208
$mids
[1] 10 30 50 70 90 110 130 150 170 190
$xname
[1] "sunspot.year"
$equidist
[1] TRUE
attr(,"class")
[1] "histogram"
出力結果を抜粋して、意味は以下の通り
| 変数名 | 意味 |
|---|---|
| $breaks | 階級の区切り |
| $counts | 度数 |
| $mid | 階級値 |
相対度数は度数の割合を出す。
累積度数、累積相対度数は度数、相対度数を順に足して行けばOKなので、
# 度数を変数に
sun_counts <- hist(sunspot.year,plot=F)$counts
# 相対度数
sun_relative_freq <- sun_counts / sum(sun_counts)
sun_relative_freq
[1] 0.301038062 0.211072664 0.152249135 0.134948097 0.072664360 0.062283737 0.034602076
[8] 0.024221453 0.000000000 0.006920415
# 累積度数
sun_cumulative_freq <- cumsum(sun_counts)
sun_cumulative_freq
[1] 87 148 192 231 252 270 280 287 287 289
# 累積相対度数
sun_cumulative_relative_freq <- cumsum(sun_relative_freq)
sun_cumulative_relative_freq
[1] 0.3010381 0.5121107 0.6643599 0.7993080 0.8719723 0.9342561 0.9688581 0.9930796 0.9930796
[10] 1.0000000
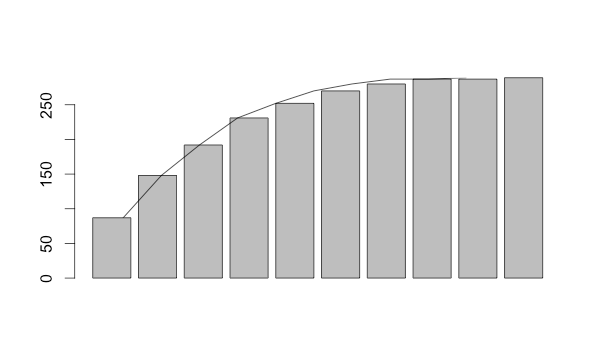
累積度数グラフを書いてみる
なんかそれっぽいの出てきた。
累積のbarplotとlinesをまとめて表示。
barplot(sun_cumulative_freq)
lines(sun_cumulative_freq)
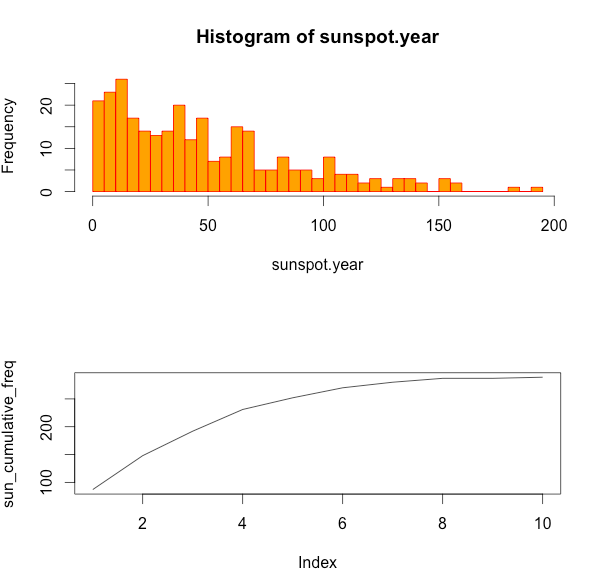
ヒストグラムと並べてみる
う、うーん。
並べる意味あんのかこれ。
par(mfrow=c(2,1))
hist(sunspot.year,breaks=50, col = "orange", border="red")
plot(sun_cumulative_freq,,"l")
ローレンツ曲線を描いてみる
r-de-rさんにご指摘いただいて図を修正
データ数1000個で偏りのあるサンプルデータを生成しました。
生成方法はrnormを調整して適当に。
標準偏差は150で固定
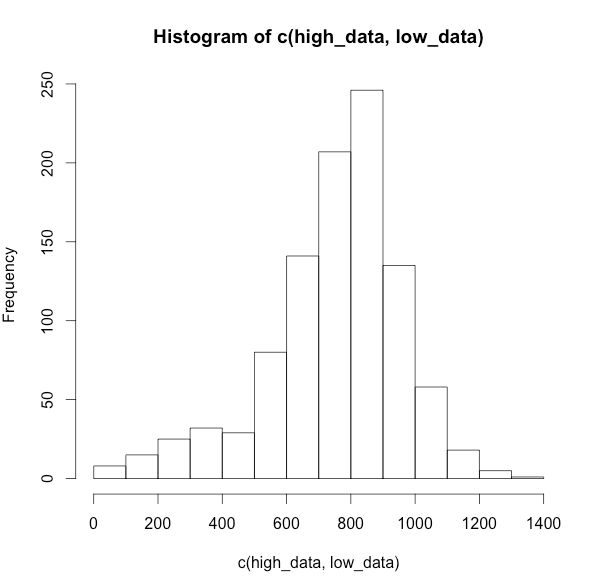
1.ヒストグラムが左に歪むもの
# 900個のサンプルデータを値高めの800で
high_data <- abs(rnorm(900,800,150))
# 100個のサンプルデータを値低めの300で
low_data <- abs(rnorm(100,300,150))
# データ結合してヒストグラムを書く
hist(c(high_data, low_data))
# ローレンツ曲線を書く準備
x <- cumsum(hist(c(high_data, low_data),plot=FALSE)$counts / sum(hist(c(high_data, low_data),plot=FALSE)$counts))
y_tmp <- hist(c(high_data, low_data),plot=FALSE)$counts * hist(c(high_data, low_data),plot=FALSE)$mids
y <- cumsum(y_tmp / sum(c(high_data, low_data)))
# 描画
plot(x,y,type="l",xlab="data_count",ylab="data_value")
# par(new=T)
# plot(0:1,0:1,type="l",col="blue")
# 高水準のplot関数にlinesで線を追加する事で軸が二重に描画されないようにする
lines(0:1,0:1,col="blue")
ヒストグラム
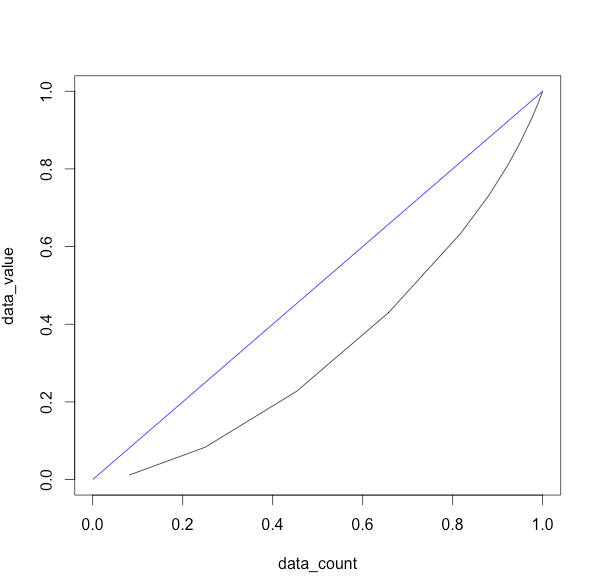
ローレンツ曲線
青はy=xの格差がない状態
黒がローレンツ曲線
想定通りの線がでました
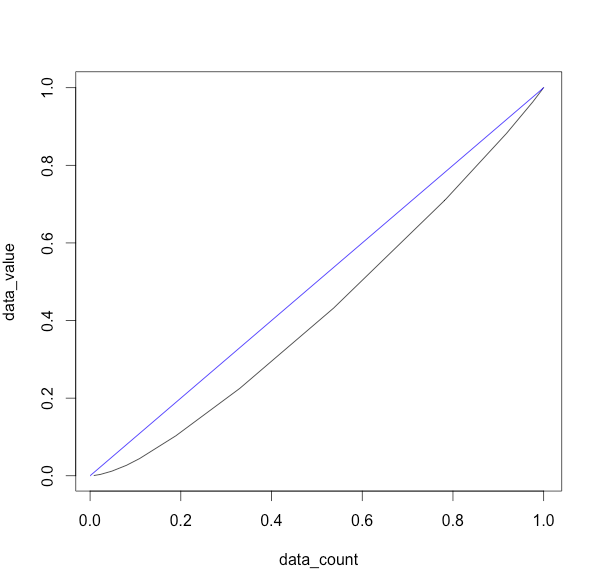
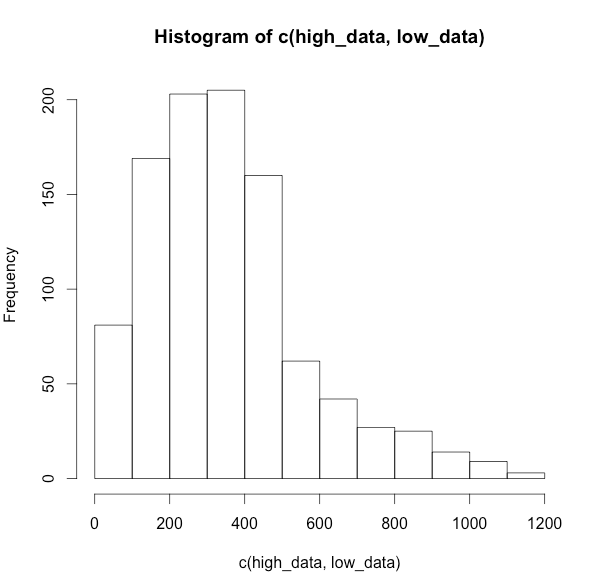
2.ヒストグラムが右に歪むもの
※データの作り方だけ異なり、ほかは同様
# 100個のサンプルデータを値高めの800で
high_data <- abs(rnorm(100,800,150))
# 900個のサンプルデータを値低めの300で
low_data <- abs(rnorm(900,300,150))
# その他のコマンドは同様
ヒストグラム
ローレンツ曲線
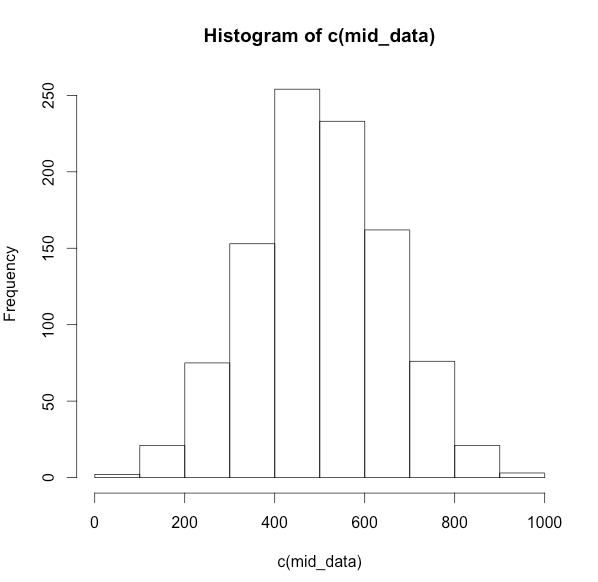
3.ヒストグラムがほぼ左右対称になるもの
mid_data <- rnorm(1000,500,150)
hist(mid_data)
ヒストグラム
ローレンツ曲線
ほぼまっすぐになると思ったのだが、分布の歪みがどうあれ格差があるのでこの結果は妥当なのかな。
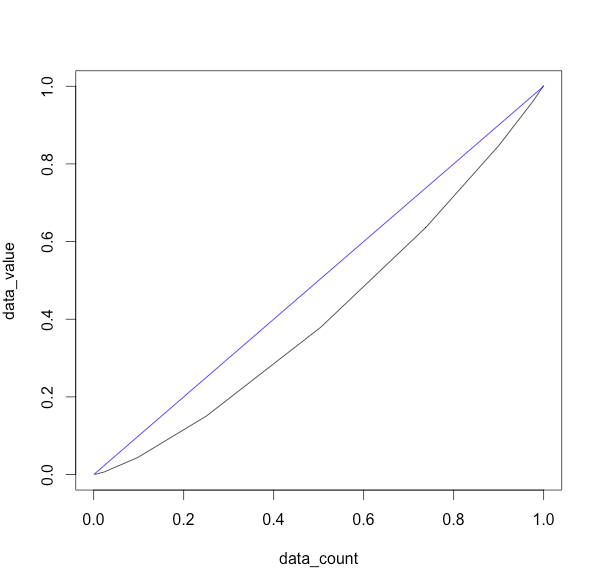
4.一様な分布の場合
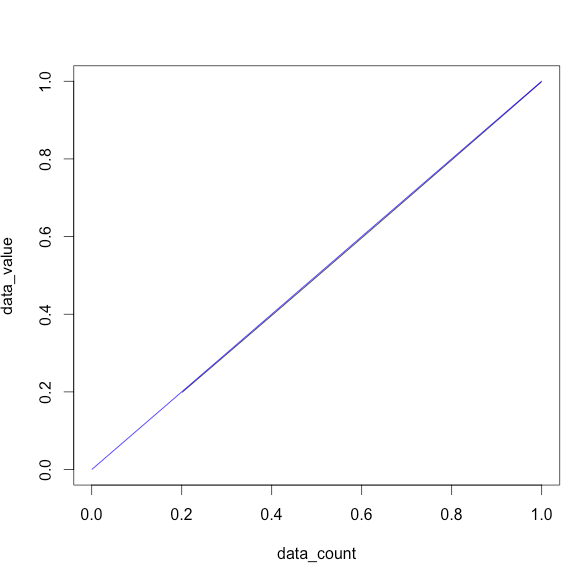
runif関数をつかって395から405の間でほぼ一様な分布を作る
uniform_data <- as.integer(runif(1000,395,405))
hist(uniform_data)
ヒストグラム
ローレンツ曲線
学べた事
- 分布からサンプルデータを求める方法
- ローレンツ曲線の特性
- 右に歪む場合上に凸になると思っていた・・・。
思ったこと
- ヒストグラムと累積度数グラフの使い分けはいつ?
- 双峰型データの検知は階級数を高めればわかるのか?実データで試したい。
- 確認出来なかったので次やりたい。
今回使ったRコマンド
※別途1記事にまとめて行きます。
参考資料
統計学入門 (基礎統計学)
Rによる優しい統計学
岩波データサイエンスvol1
LinkData
トライフィールズRデータ一覧
leaflet
はじめてのR(その4)
統計解析フリーソフト R の備忘録頁 ver.3.1 55. 複数の図