仮説:モナドとはポケモンである
このテキストは、でんこうせっかの速さでモナドが使えるようになりたいひとのための、真面目なモナド入門です。数学っぽい話はなるべく避けていますし、関数型言語についての知識がなくても読めるように書いています。対象の読者は以下のような人です。
- モナドが何なのか知りたい、使いたい
- Haskellを学ぼうとしたがモナドがわからなくて挫折した
- モナドを学ぼうとしたら、箱だのブリートだのと変な喩え話をされて余計わからなくなった
- プログラミングを学ぶつもりが数学の講義が始まったので止めた
- 最初はモナドは難しいからとGHCiを使わされたが、電卓程度にしかならないので飽きた
なお、何故か説明の補助としてポケモンが登場しますが、この記事を読むのに別にポケモンをプレイしたことがある必要はありません。この記事はもしポケモン要素を全部無視したとしてもわかるようになっています。
挿絵があったほうが楽しいと思ったので、ポケモンだいすきぬりえを使ってみんなが大好きなピカチュウを描いてみました。けっこう可愛く描けたと思います。
モナドの図鑑を眺めよう
モナドは難しくありませんし、複雑でもありません。なぜなら、たったふたつの関数だけで説明がついてしまうからです。ただ、モナドはとても抽象的な概念なので、取り組み方を間違えるとさっぱり要領が掴めず学習に苦労するはずです。特に、以下の様な遠回りの学びかたをしているひとが多くいる気がします。このような学び方は止めておきましょう。
- 「モナド」でググって、モナドを解説しているブログを片っ端から読み漁る
- 質問サイトで『モナドとは何ですか?』と質問してみる
- モナドの定義やモナド則とにらめっこして、それが何を意味しているのか頑張って頭のなかで考えぬく
- 関数型でない言語を使ってモナドの移植に取り組む
- プログラミングのモナドが数学の圏論に由来するという豆知識を聞きかじり、数学書を開いて圏論に学ぼうという高尚な志を抱く
- 新しい概念を学ぼうとせず、自分が既に知っている何らかのプログラミング知識に照らし合わせようとする
- 箱とかブリートとかポケモンとか、何かの比喩として理解しようとする
モナドに限りませんが、抽象的な概念を学ぶコツは具体例を数多く学ぶことです。「ポケモン」が「ピカチュウ」や「ラッタ」といった具体的なポケモンの総称であるように、モナドとはMaybeモナドやListモナドといったモナドの**具体例**の総称です。モナドを理解するには、なによりモナドのインスタンスを数多く知り、それぞれのモナドの具体例を使えるようにすることが大切です。モナドの具体例をいくつも知れば、やがてその共通点としてモナドとは何なのかが見えてきます。
「モナドについて学んでみたが、よくわからなかった」という人がいたら、モナドの具体例を5つ挙げてみてください。もしそう言われて即座に5つ答えられないようでは、それは「モナドを学んだことがある」という段階とすら言えるかどうか怪しいところです。個々のモナドがすぐに挙げられないようでは、モナド全体の理解など程遠いです。「ポケモンの名前5つ答えてみて」と言われて答えられないようでは、「ポケモンをやったことがある」と言えるのかどうかというレベルでしょう。それと同じです。
それでは、まずはモナドの図鑑をパラパラとめくって、駆け足でいろんなモナドを眺めてみましょう。
Maybeモナド
プログラミングでは、操作が必ずしも成功するとは限りません。例えば、リストの要素への参照では、インデックスが範囲内なら成功してその要素を返せますが、そうでないなら失敗になります。あるいは、文字列中の別の文字列の位置を調べるindexOfも、その文字列が見つかればインデックスを返せますが、そうでなければ失敗になります。
ここではリストxsへのi番目の要素へのアクセスを、!!という演算子を使ってxs !! iというように表すことにします。また、文字列xの位置を文字列yの中から探す操作をindexOf x yと書くことにします。このような失敗しうる計算が何度か続くとき、Haskellライクな言語では例えば次のように表すことができます。
x <- ["Space", "World", "Universe"] !! 1
y <- indexOf x "Hello, World"
pure ("String \"" ++ x ++ "\" at " ++ show y)
このプログラムは次のような順序で計算が進んでいきます。
1.["Space", "World", "Universe"] !! 1という式でリストの1番目の要素を参照し、結果である値Worldに変数xが束縛されます。
2. 次にindexOf x "Hello, World"という式が計算され、結果である7という値に変数yが束縛されます。
3. 最後に"String \"" ++ x ++ "\" at " ++ show yが計算され、これがpure関数に渡されます。
4. この最後の行の値が、この一連の計算全体の結果になります。
まあ上から下に順番に計算が行われていったというだけなのですが、この一連の計算の途中で失敗が起こるともっと興味深い振る舞いになります。たとえば、2行目で"World"という文字列を検索するときに、どうみても"World"が含まれていないような文字列を与えてみます。
x <- ["Space", "World", "Universe"] !! 1
y <- indexOf x "----"
pure ("String \"" ++ x ++ "\" at " ++ show y)
このとき、計算がindexOf x "----"のところまで来ると、この計算は失敗し、そこで一連の計算は中止され、呼び出し元に失敗したという情報のみが伝わります。一連の計算が失敗した時点で、この計算を中止して呼び出し元に戻るのです。これは単にプログラムがクラッシュしたとかではなくて、呼び出し元は計算が成功したか失敗したか、結果を条件分岐して調べて、安全にプログラムの実行を継続することができます。
また、Nothingという値を使うと、その地点で確実に計算を失敗させることができます。次のコードでは、必ず二行目で計算が失敗し、そこで計算が中止され、呼び出し元に戻ります。
x <- ["Space", "World", "Universe"] !! 1
Nothing
pure ("String \"" ++ x ++ "\" at " ++ show y)
そういえば、一番最後の行ではpureという関数を呼び出していますが、これは必ず成功する『失敗しうる計算』を表現するためのものです。x + y + zという普通の計算を、pure関数に渡すことで、!!やindexOfのような操作と同種の計算として扱えるように変換しているのです。
つまり、この一連の『失敗しうる計算』はシンプルな例外処理機構として働きます。途中で失敗すればそこで計算を中止し、呼び出し元では計算が最後まで成功したかどうか、それとも失敗したかどうかわかります。また最後まで成功した場合はその結果の値もわかります。Nothingを挟めば、まるでthrowで例外を投げるように途中で計算を中止できます。Maybeモナドというのは、このような構文を実現するものです。Maybeモナドはモナドを学び始める時にだいたい最初に扱うシンプルなモナドで、物語序盤でみんなが遭遇し、最弱クラスだけど最弱ではないポケモン、**コラッタ**のような存在です(強引)。
ここではこれ以上Maybeモナドの詳細には踏み込みません。ここでよく確認しておきたいのは、このMaybeモナドの振る舞いでも実装の詳細でもなく、次の2点です。
結果 <- 何らかの同種の計算という文の連続として一連の計算を表現できることpure関数で任意の式をその計算に組み込めること
Eitherモナド
Maybeモナドは失敗して計算が中止しても、呼び出し元がなぜ計算が失敗したのかを窺い知ることはできません。失敗した時にその理由を呼び出し元にちゃんと伝えたいという場合は、次のEitherモナドを使います。
JSONオブジェクトのプロパティを読み取る関数readIntProp、readStringProp、readBooleanPropのような関数があったとしましょう。これらの関数は、引数に指定した名前のプロパティが存在しない時や、読み取ろうとしたプロパティのデータ型が一致しない場合に失敗になります。コードは例えば次のようになります。
x <- readIntProp "x" json
y <- readStringProp "y" json
z <- readBooleanProp "z" json
pure { x: x, y: y, z: z }
このコードでも、上から順に一行づつ実行されていき、途中で失敗がなければ最後まで計算が進み、それから最後の行の値が最終的な結果になります。失敗した場合は、どのプロパティの読み取りに失敗したのかが呼び出し元に伝わります。
MaybeモナドではNothingで明示的に失敗させて中止することができましたが、Eitherモナドでも同じようにLeftで計算を中止できます。ただし、Leftは関数になっていて、引数に受け取ったデータを呼び出し元に伝えることができます。この点がMaybeモナドとの違いです。
x <- readIntProp "x" json
y <- Left "Some error" -- 計算はここで中止され、"Some error"という例外情報が呼び出し元に伝わる
z <- readIntProp "z" json
pure { x: x, y: y, z: z }
これはつまりEitherモナドは、Maybeモナドと同様の機能を備えているだけでなく、その自然な拡張になっています。ポケモンで言えばコラッタの進化系である**ラッタ**であるといえるでしょう。Haskell/PureScriptはtry-catch文のような例外処理専用の構文を持たないのですが、まさにthrow文と同じようにエラーオブジェクトと共に計算の途中で抜けるという振る舞いが、このEitherモナドで実現できるのです。
さて、ここでも重要なのはEitherモナドの振る舞いや機能ではなく、このモナドもまた**『結果 <- 計算という文の連続として計算を表せること』『pure関数で任意の値をその計算に組み込めること』**という共通点を持っていることです。
リストモナド
リストモナドとは、それぞれの計算が複数個の結果を持つような計算を表すことができるモナドです。リストモナドでは名前の通りそれぞれの行の計算がリストであるような式になっていて、このリストの要素がそれぞれの計算の結果だと考えます。例えば、次のようなコードを書くことができます。
x <- [1, 2, 3]
pure (x * x)
このコードは次のように振る舞います。
- 最初の行
[1, 2, 3]の最初の値1にxが束縛されます。 - 最後の行で
x * x = 1 * 1 = 1が計算される - 最初の行
[1, 2, 3]の次の値2にxが束縛されます。 - 最後の行で
x * x = 2 * 2 = 4が計算される - 最初の行
[1, 2, 3]の次の値3にxが束縛されます。 - 最後の行で
x * x = 3 * 3 = 9が計算される - これまで最後の行で計算された結果がリストにまとめられて、全体の結果になる
この計算では不思議なことに、最後の行が3回実行され、それらの結果すべてがリストにまとめられて結果として変えるのです。行がもっと増えると、それぞれの行の要素すべてに網羅的に計算が行われます。
x <- [1, 2, 3]
y <- [7, 8]
pure (x + y)
例えば、このコードでは、一行目は3つの値、二行目は2つの値があるので、最後の行は2 * 3 = 6回の計算が行われ[8, 9, 9, 10, 10, 11]という値として呼び出し元に返ってきます。
このモナドの特徴的な点は、それぞれの行の計算が、必ずしも上から順に一回づつ計算されていくというわけではない点です。それぞれの計算が複数値を返すことができ、それらのすべての場合について網羅的に計算が行われます。これはまるで、れんぞくパンチで1ターンに複数回攻撃する**ガルーラ**のようです。
MaybeモナドやEitherモナドは途中で中止されることがありましたし、リストモナドは同じ行を何度も計算することがあります。モナドがどのような順序で計算を進めていくのかは、それぞれのモナドによってまったく異なるのです。しかし、ここではモナドの共通点を探すことが重要でした。リストモナドがたとえこのような不思議な順序で計算が進むとしても、**「結果 <- 計算という文の連続で一連の計算を表すことができること」「pure関数で値を計算に組み込めること」**という2点には変わりはありません。今回重要なのはそこです。
STモナド
Haskellのような言語は変数の再代入禁止だとか聞いたことあるかもしれませんが、STモナドを使うと、どのオブジェクトも変更禁止、変数の再代入禁止という純粋な計算の中でありながら、変更可能な状態を作り出して計算することができます。
モナドの計算の中では、それぞれモナドの種類に応じた機能が使えます。MaybeモナドではNothingが、EitherモナドではLeftが、独自の操作として使うことができました。リストモナドでは[1, 2, 3]のようなリストリテラルをそのまま書けましたし、結果がリストになる式は何でも計算の中に組み込むことができます。そして、STモナドではnewSTRef、modifySTRef、readSTRefなどの多彩な関数を使うことができます。newSTRefは変更可能な領域を作り出す関数で、C++でいうところのnew演算子でヒープを確保しているようなものです。またmodifySTRefではこの領域の値に対して任意の変更を加える事ができます。そしてreadSTRefではその領域の値を読み出すことができます。
例えば、リストxsの値の合計をSTモナドで求めると、次のようになります。
n <- newSTRef 0
for xs $ \x ->
modifySTRef n (_ + x)
readSTRef n
ここで、領域nに格納された値は、forでの繰り返しの中で事実上繰り返し変更されていると捉えることができます。一見変更できないオブジェクトの不変性がありながら、内部で自由に変更可能なオブジェクトを提供するSTモナドは、まるで外側は固くて歯がたたないけど中は柔らかい**シェルダー**にそっくりです(強引)。
Identityモナド
Identityモナドは せかいで いちばん よわくて なさけないモナドです。酷い言われようですが、何しろこのIdentityモナドはpureくらいしかできることがありません。**モナド界のコイキング**とはIdentityモナドのことです。MaybeみたいにNothingで処理の途中で抜けたりはできませんし、リストモナドのように何度も計算を繰り返したり、STみたいに状態を変えていくこともできません。pureで計算に組み入れることはできても、それがそのまま<-で出てくるだけです。本当にそれくらいしかできません。
x <- pure 10
y <- pure 20
z <- pure 30
pure (x + y + z)
何も役に立つことはできそうにありませんが、「結果 <- 計算という文で表せる」「pureを使える」というモナドの共通点はしっかり満たしています。何もできないけどポケモンには違いないし枠を埋めることはできるコイキングみたいに、何もできないけどモナドには違いない、そういう感じの変なモナドです。このモナドは単独ではほとんど意味がなく、他のモナドの内部に埋め込まれることで真価を発揮します。
Freeモナド
このモナドはポケモンで言うと**メタモンのような、それ自身では何もできないが、どんなモナドにも変化することができるという、とにかくメタメタしい性質を持っています。不思議なことに、このFreeモナドをへんしんさせれば、Maybeモナドでもリストモナドでも、どんなモナドも創りだすことができるのです。これを説明しだすと長くなるので割愛しますが、とりあえずメタモンもポケモン**ということだけ頭に入れておけば大丈夫です。
メタモンかわいいよメタモン
IOモナド
IOモナドはreadFile関数でファイルの読み取り、putStrLn関数で標準出力など、外界とのあらゆるやりとりを一手に担うとても機能の多いモナドです。また、Eitherのように例外を投げて途中で脱出したり、STモナドのように変更可能な領域を作り出すことすらできます。
また、IOモナドはプログラムのエントリポイントとなるモナドであり、現実のコードだとこのIOモナドはプログラム全体にわたって登場し、ユーザはIOとは切っても切り離せない関係を築くことになります。まさにアニメ版ポケモンで主人公サトシが強制的に選ばされることになり、ボールに入るのが嫌などという言い訳でとにかく画面に映りたがる**ピカチュウ**のようなモナドといえます。
例えば、標準入力から指定した名前のテキストファイルをコピーする計算は次のようになります。
from <- getLine
to <- getLine
putStrLn ("copy " ++ from ++ " to " ++ to)
contents <- readFile from
writeFile to contents
このモナドも、**「結果 <- 計算という文の連続で一連の計算を表すことができること」「pure関数で値を計算に組み込めること」**という2点は満たしています。それを確認しておきましょう。
それで、モナドとはつまり何なのか
さて、モナド全体に共通するのは、次のたった2つの点だけでした。
-
結果 <- 何らかの同種の作用の連続で一連の計算が表現される -
pure関数で任意の値を計算に組み込める
そして、どのモナドも、あくまでこの枠組みの中にありながら、それぞれ異なるわざを持っていたのでした。
- Identityモナドは
pure以外には何もできない最弱のモナドです - Maybeモナドは
Nothingで計算の途中で抜けるという機能だけを持つとても弱いモナド - Eitherモナドは
Leftで計算の途中で脱出でき、その時追加の情報を持ち帰ることができる、Maybeよりちょっと強いモナド - リストモナドはそれぞれの計算が複数個の値を返すことができ、それらすべての値について繰り返し計算を行えるという独特の能力がある
- STモナドは
newSTRefで変更可能なデータ領域を好きなだけ作りだし、それをmodifySTRefで変更したりできます - IO/Effectモナドは
readFileファイル操作したりprintで標準出力したりといった機能のほか、throwErrorのようなEitherモナド相当の機能や、newIORefのようなSTモナド相当の操作もできる万能モナド - Freeモナドは最弱のモナドから最強のモナドまで何にでもへんしんできるモナド
つまり、ひとつの見かたとしては、モナドとは計算の中で使える操作や計算の過程を自由にカスタマイズできる領域特化言語を実現するための枠組みであると捉えることができるでしょう。
モナドによる抽象化は、
var 変数 = 式;
var 変数 = 式;
var 変数 = 式;
...
というような構文をカスタマイズできるようにしたもの、という見かたもあって、プログラム可能なセミコロンなどと説明されることもあります。文と文のあいだに置かれるセミコロンを一種の中置演算子だと考えて、このセミコロン演算子を演算子オーバーロードしてるようなものだ、というわけです。
HaskellやPureScriptはこの枠組みをコード全体に渡って一貫して再利用し、これらのモナドを目的に応じて使い分けて計算を進めていく言語なのです。このため、Haskell/PureScriptにはthrow/catchのような例外処理の専用の構文がないのに例外を投げて計算の途中から脱出したり例外を捕まえたりすることができるし、await/asyncもないのに非同期処理を同期的処理と同じように平坦に書くことができるのです。
そして、目的に合わせてカスタマイズした専用のモナドを自分で作って使うこともできるという、強力な拡張性も備えています。モナドを自分で定義すると、どんな操作を許しどんな操作を許さないか、何もかもを自分でコントロールできます。
やさしいモナドの使いかた
プログラミングにおけるモナドはコーディングの道具であって、理論を鑑賞して悦に浸るためのものではありません。使わなければ何の意味もないのです。ここからはモナドを使ったコードをどのように書けばいいのかを具体的に説明していきます。
さて、モナドにはいろいろな種類があり、それぞれ違った能力を持ちますから、まずは自分の計算の目的に応じて適切なモナドを選ばなくてはなりません。使いたいモナドがすぐに思いつくように、モナド図鑑をよく頭に入れておくことが大切です。ここでは説明のためにIOモナドを使ってみます。HaskellではIOモナド、PureScriptではEffectモナドは、唯一絶対に避けて通れないモナドになっています。これらの言語で実用的なコードを書くにはどうしてもIO/Effectだけでも使えるようになるのが先決ですし、ひとつでも使えれば他のモナドへの足がかりにもなります。
do式の一般形
これまで何度も見てきた結果 <- 作用というような文の連続からなる構文は、do記法と呼ばれています。このdo記法を使いこなせるようになっておくことが、モナドを実用に供する上で必要不可欠です。これまで見てきたとおり、do記法の構文は外見上結果 <- 作用でほとんどすべてという単純さなのですが、実はコードの字面に現れない隠れたルールこそが厄介です。
Haskellでは、コード中で式の型を明示するのに、ダブルコロン::を使って次のように書きます
式 :: 型
また、型変数aを含むような型mは、単にスペースを挟んで次のように書きます。
m a
これを使って、do記法の中の式にもれなく型注釈を書き込むと、do記法の一般形は次のようになります。
(do
v0 :: a <- expr0 :: m a
v1 :: b <- expr1 :: m b
v2 :: c <- expr2 :: m c
...
exprZ :: m z) :: m z
このmの部分にはモナドに結び付けられた型の名前が入ります。IOモナドを使う場合は、mをIOに置き換えて、次のようになります。
(do
v0 :: a <- expr0 :: IO a
v1 :: b <- expr1 :: IO b
v2 :: c <- expr2 :: IO c
...
exprZ :: IO z) :: IO z
このIO aは、それがIOという種類の操作であり、その結果としてa型の値を返すことを意味しています。
ルール1 頭にdoをつけてインデントを揃える
図鑑の擬似コードでは省略していましたが、do記法では先頭にdoというキーワードを付けます。また、そのdo記法内部の式はインデントを揃えなくてはなりません。
ルール2 結果はそこから下に書かれた計算の中でのみ使える
それぞれの計算の結果は、それ以降の計算の中でしか使うことができません。
do
v0 <- expr0
v1 <- expr1
v2 <- expr2
exprZ
このようなコードでは、例えば変数v1はそれより前の式であるexpr0、expr1の中からは参照することはできません。それより後ろにあるexpr2、exprZの中からのみ参照できます。これは普通の言語で変数に値を代入するときの振る舞いと同じです。
ルール3 結果を束縛する変数は省略できる
各行の結果 <-という部分は省略可能です。たとえば、標準出力を行う関数putStrLnの結果の型は()になっていますが、これはC言語でいうvoid型みたいなもので、データには何の意味もありません。このような操作の結果を変数に束縛するのは無意味なので、結果 <-という部分は省略することができます。()型に限らず、操作の結果が不要ならどの行でも自由に省略してしまって構いません。
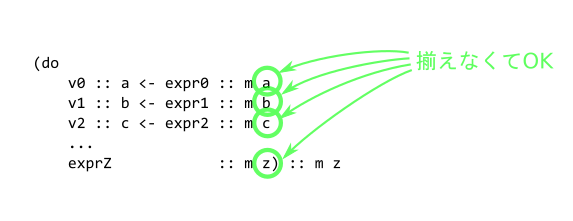
ルール4 最後の行は結果を束縛できない
最後の行では結果 <- 式というように<-を使って書けません。その最後の行の結果が、Do記法全体の結果になるからです。
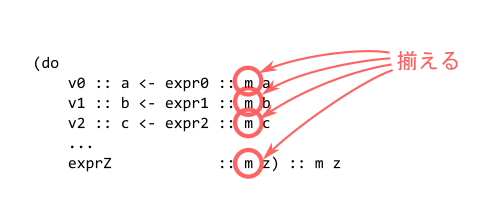
ルール5 型構築子は統一する
これは何を言っているかというと、以下の丸をつけた部分の型は、すべて同じでなくてはならないということです。
つまり、MaybeモナドとEitherモナドのように異なる種類のモナドの計算を、直接は混ぜることはできないということです。なお、この型構築子に与えられた、操作の結果の型のほうは、それぞれの行でバラバラで構いません。
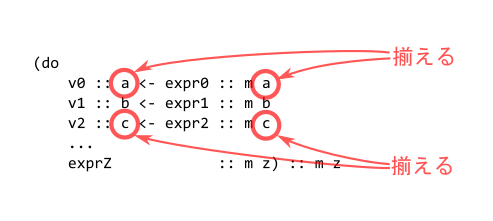
ルール6 計算の結果の型を一致させる
<-の右側の式の型m aは、その計算の結果はa型になるということを意味しています、これは以下の丸をつけた部分の型は、それぞれ一致していなければならないということです。
ルール7 最後の行とDo式全体の型を一致させる
do式はそれ全体が式であり、その型はdo式の最後の行の式と一致していなければなりません。この最後の式の値が、do式全体の計算の結果になるからです。
ドキュメントを漁る
さて、実際にモナドを使うには、どんな操作が可能なのかをドキュメントで確認する必要があります。たとえば、Haskellではデフォルトでインポートされる標準モジュールPreludeに標準出力を行う関数や簡単なファイル操作を行う関数が定義されています。
関数なら引数を与えて最終的にIO aというような形になればdo記法の中に書けますし、中にはそのままでIO aという値を持つ値もあります。これらをドキュメントから探します。ここでは次の関数や値を使うことにしましょう。
readFile :: FilePath -> IO String
writeFile :: FilePath -> String -> IO ()
getLine :: IO String
putStrLn :: String -> IO ()
いずれも、型注釈の最後がIO aという形になっていることがわかるでしょう。これらはすべてIOモナドの計算のなかで使える操作だということです。
完全なコードのサンプル
これらの関数を使って、テキストファイルのコピーを行うプログラムを作ってみます。標準入力から、コピー元のファイル名とコピー先のファイル名を読み取り、それらの名前に従ってファイルをコピーします。
main :: IO ()
main = do
from :: String <- getLine :: IO String
to :: String <- getLine :: IO String
putStrLn ("copy " ++ from ++ " to " ++ to) :: IO ()
contents :: String <- readFile from :: IO String
writeFile to contents :: IO ()
先に挙げたルールが守られていることを確認してみてください。
ここでは説明のために過剰に型注釈をつけていますが、これらはすべて型推論可能なので、次のようにすべて取り去ってしまっても大丈夫です。
main = do
from <- getLine
to <- getLine
putStrLn ("copy " ++ from ++ " to " ++ to)
contents <- readFile from
writeFile to contents
モナドのはじめかた
自分がモナドを理解できたかどうか確かめる唯一の方法は、自分で実際にコードを書いてみることだけです。もしモナドをなかなか理解できないなら、その最大の原因は自分でモナドを使ったコードを書こうとしていないからだと思います。啓蒙的な記事ばかりを幾つ読み漁ったところで、モナドは理解できません。なぜなら、自分でモナドを使ったコードを書いていないからです。モナドの定義を穴が空くまで眺めても、モナドは理解できません。なぜなら、自分でモナドを使ったコードを書いていないからです。多分この記事を開いたひとはみんなモナドを理解したいんだろうと思います。まずはコードを書いてみましょう。
Haskell
Haskellのインストールは、現状はStack一択です。インストールも難しくないのでさくっとインストールしてしまいましょう。
PureScript
PureScriptのインストールはnpmが入っていればnpm install purescriptで一発です。ただし素のコンパイラは色々下準備が大変なので、pulpというツールを使ってビルドするのが一番手っ取り早いと思います。
PureScriptは後発なだけあってライブラリがよく整理されていて、モナド周辺についても、年季が入ったHaskellのライブラリ群よりわかりやすいと思います。PureScriptのライブラリ群は、Pursuitというドキュメント検索エンジンで眺めてみるのが手っ取り早いです。
その他の言語
上記以外の言語ではモナドの威力を十分に引き出せません。やめておきましょう。
それで結局モナドの何が嬉しいのか
モナドの存在意義について「言語全体の式から副作用を排除したので、そのかわりモナドを導入して副作用を扱えるようにした」みたいに紹介されることがありますが、じゃあ最初から副作用アリにしとけばモナドなんて小難しいもの要らんやんけ!と思う人も多いんじゃないでしょうか。導入された当初のきっかけは確かにそれだったみたいなんですが、いろんなものがモナドとして扱えることがわかってきた現在では、単に純粋な言語の上で副作用を扱うためという以上のメリットがモナドにはあると思います。
わかりやすいところを挙げるなら、他の言語では言語の構文を拡張してようやく導入されるような機能を、言語じたいを変更することなく、単なるライブラリを追加するだけで実現できるということがあります。
- async/awaitが言語仕様になくても、
affパッケージを導入すれば非同期処理を平坦に書ける! - 例外処理機構が言語仕様にないのに、
exceptionsパッケージを導入すればthrow関数で例外を投げてtry関数で例外を捕まえることができる! - リストの内包表記がなくても、
listsパッケージを導入すればリストモナドで同様のことができる!(構文の見た目はかなり異なりますが) - 配列の要素を一部だけ書き換えるような構文はないのに、
stパッケージを導入すればpokeSTArray関数で配列の一部を書き換えての処理ができる! -
refsパッケージを導入すれば、writeRef関数で変数の中身を書き換えられる!
もちろん、特別な構文が欲しくなったらその都度言語仕様を改良してコンパイラを改造するという方法もあるでしょう。でもそのためには数ヶ月とか数年がかりの議論と、コンパイラ自体を改造する労力が必要になるでしょう。でもモナドで作用を抽象化してある言語なら、ひとつライブラリを作るだけで済みます。それに、新しい構文を導入してみたけど使ってみたら使いにくくてやっぱり要らないねとか、もっと新しい方法が出てきたので古い構文は要らないね、みたいなこともあるでしょう。でもいったん言語仕様に組み込んでしまったらそうそう廃止することはできません。言語は複雑になっていく一方です。でもただのライブラリなら廃止もはるかに簡単です。
モナド則とか学ぶな
巷の『モナド入門』の多くは、『モナド則』なる数学っぽい規則を説明します。あまりに抽象的で初心者殺しのモナド則ですが、実は初心者はまったく知る必要のない知識だったりします。
モナド則というのはモナドのインスタンスを定義するときに守らなければならない規則であって、すでに定義されたモナドを使うときにはモナド則は勝手に満たされています。そして、Haskell/PureScript/Scalaあたりならモナド関連のライブラリは豊富に揃っているので、自分でモナドのインスタンスを定義する機会はまずありません。モナド則が必要になる時というのは、今まで誰も作ったことのない新たなモナドを思いついたということで、それはとても高度なトピックです。既存のライブラリにないような新しいモナドを思いつくというのは、まったく新しいソートアルゴリズムを考案したとか、まったく新しいデータ構造を考案したとか、そういうレベルの話です。普通はそこまでの知識は必要になりません。
しかも、モナドの実装がちゃんとモナド則を満たしているのかを確認する簡単な方法はありません。そのため、Haskellの標準ライブラリで提供されていたListTというモナド(正確には『モナド変換子』)がモナド則を満たしていないというバグが後になって発覚したということが実際に起きています。関数型プログラミングに習熟した人でさえ、うっかり間違えてモナド則を破ることがあるのです。こんな難解なトピックに初心者が取り組む必要はまったくありません。
もちろん知識としてモナド則を知っているに越したことはないですし、自分でモナドのインスタンスを定義してみるとより深い理解を得られるとは思います。数学的なことが好きな人は、そのあたりの概念について学んでみると面白く感じるでしょう。でも、モナド則の理解につまづいて関数型プログラミングの習得を諦めたりするくらいなら、そんなものさっさと飛ばして、実際にモナドを使う練習をしたほうがよほど理解につながります。
さまざまなモナドを地道に泥臭く学んでついにモナドの概念を身につけた人の中には、「『モナドとはなにか』はモナド則を見ればぜんぶわかるはず」などとスマートなことを言ってみせて格好つけるキザな人も少なくないようです。確かにモナドの定義はモナド則で述べられている通りで、言っていること自体は間違いとまでは言えませんが、モナド則だけ見て理解できる天才なんてほんとに一握りです。それ以外の普通の人は地道にいろんな具体的なモナドを実際に使ってみることでようやく理解に至っているはずです。そんなキラキラしたスマートでオシャレな入門は普通の人間にとっては近道なようで遠回りですから、それぞれのモナドを実際に使ってみて、地道に学びましょう。
結論:モナドはポケモンではない
モナドとは、結果 <- 作用という文の連続からなる計算を、その計算の中でどんな作用(操作)が可能か、どの順序で計算が進むかを自由に制御可能にするための枠組みです。先ほど見た7つのモナドでは、IOモナド以外はすべて自分で定義することが可能です。自分のやりたい計算に合わせてカスタムメイドのモナドを定義することもできます。この枠組ひとつあれば、for文のような繰り返しも、try-catch文のような例外処理機構も、書き換え可能な領域も、async/awaitのような非同期処理や、文字列の構文解析に特化したDSLまで、すべては自分で作り出せるのです。
どんなに定義を眺めても、箱だとかポケモンだとかいうメタファーに頼ってみても、あまりモナドの理解には繋がりません。それぞれのモナドを実際に使ってみて、あなたのモナド図鑑をひとつひとつ地道に埋めていくことが、モナドマスターへの唯一の道だと言えるでしょう。
ポケモンマスターはいろんなポケモンを使いこなすことができますが、初心者ポケモントレーナーが「自分がポケモンを使いこなせないのは、自分がポケモンマスターでないからだ。ポケモンを使えるようになるために、まずはポケモンマスターになろう」って考えたとしたら、それは因果関係が逆です。ポケモンマスターになったからポケモンを使えるのではなく、ポケモンを使えるからポケモンマスターなのです。同じように、モナドを理解したからモナドのインスタンスを使いこなせるのではなく、それぞれのモナドのインスタンスを使いこなせるようになったからこそ、モナドを理解したモナドマスターになれるわけです。どんな初心者トレーナーも最初はコラッタから捕まえていくように、まずはそれぞれのモナドを書いて地道に練習していきましょう。
おすすめ文献リンク集
まずは自分でコードを書いてみることが第一ですが、もちろん文献もモナドを理解するうえで欠かせないものです。筆者の個人的なおすすめは、「モナドのすべて」を頑張って読み通すことです。
- モナドはメタファーではない - モナドはメタファーではない!繰り返す!モナドはメタファーではない!だからモナドをポケモンに例えるのも不可能!知ってた!
- モナドのすべて――Haskell におけるモナドプログラミングの理論と実践に関する包括的ガイド - かなりヘヴィな文献ですが心配いりません。私はHaskellを使い始めたときこのテキストでモナドを学びましたから。危うく死ぬかと思いました。
- 絶対に理解出来ないモナドチュートリアル - 計算練習のようにコードを書くことが大事だ、というのは私もまったくもってその通りだと思います。
- What a Monad is not / モナドは何でないか
----------------------------------------------- キリトリセン ---------------------------------------------------------------
すごくどうでもいい補足(読む必要なし)
普段筆者は説明しすぎるきらいがあるので、長い文章が苦手な人でも読めるように今回は文章を可能な限り削ってみることにしました。当初書いた量の半分以下になっています。自分の知らない言語はたった数行でも読まない、振る舞いを類推することもしないという人もいるようなのですが、サンプルコードもひたすら切り詰めたので何とか想像して読んでください。不正確な内容についての注釈もガリガリ削ってあるので、細かいところは気にしないでください。
あとこの記事では、数学っぽい話はもちろん、「型クラス」のようなHaskell臭い機能や、Functor/Applicative/Monadという型クラス階層、モナドの定義、モナド則のような内容もごっそり省きました。型クラス階層を順に追い、定義とモナド則ファンクタ則で足元を固めていく入門は、すでにわかっている人にとっては簡潔、明瞭かつ合理的で整然とした過程に見えますが、初心者には抽象性の泥沼でしかありません。小学1年生に公理的集合論とペアノ算術を教えてから足し算を教えるような丁寧でお行儀のいい入門なんて、窓から投げ捨ててしまいましょう。モナド則に至っては、現実のコーディングではまず役に立たない知識です。理解の助けにもなりません。こんなものをさぞ大切なものであるかのように教えるのは、教える内容の優先順位を間違えていると思います。
ポケモン要素は、今年で20周年だという話を書いている途中で聞きつけて、後付けで説明に加えました。この記事べつにポケモン要素要らなくね?と思ったでしょうが、こういうのはインパクト重視です。まあこのテキストのネタかなり無理やりなので、見ての通り『モナド=ポケモン理論』は無事破綻しました。ギエピー!あと、冒頭の画像は、ピカチュウじゃなくてヤドンじゃねーか!って、はてブとかでツッコんで欲しかったのですが、誰もツッコんでくれませんでした!本当にありがとうございました!