はじめに
ここ最近は公私ともに雑多にいろんなことをしすぎていたので、久しぶりに統計のことに触れてみようと思った次第です。
環境
Mac OSX mojave
Python3.7
とりあえず超超有名な入門書
ハンバーガー統計をPythonで書いてみたいと思います。
元はこちらの内容
分量が多くなるので
①:平均と分散、信頼区間
②:カイ二乗検定
③:t検定
④:分散分析
のようなシリーズで行きたいと思います。
平均と分散
違う店舗のポテトの長さを比較するという話から平均値を求めることになりました。
総和をサンプルサイズで割るだけなので簡単ですね。
とりあえず必要そうなライブラリを入れます。基本はscipyでやります。
import pandas as pd
import numpy as np
import scipy as sp
from scipy import stats
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
%matplotlib inline
%precision 3
サンプルデータをリストにします。numpyのarrayにします。
list_wakupotates = [3.5,3.8,5.8,6.4,\
4.2,4.2,4.0,3.6,3.8,5.2,\
4.9,5.2,6.0,3.9,5.3,4.6,\
3.9,4.2,4.2,6.4,2.8,5.6,\
5.7,5.1,4.4,5.6,5.3,3.9,\
5.1,3.6,4.2,5.0,4.7,4.1,\
3.7,4.9,4.7,5.3,3.6,4.2,\
4.4,4.0,5.5,4.2,4.8,3.7,
3.1,4.7,5.0]
array_wakupotates = np.array(list_wakupotates)
次にサンプルサイズを出して、総和を出して、割ります。
$$
算術平均 = \frac{総和}{サンプルサイズ}
$$
N = len(array_wakupotates)
sum_value = sp.sum(array_wakupotates)
mu = sum_value/N #標本平均
print(mu)
4.571428571428571
これ一発で出ます。
sp.mean(array_wakupotates)
4.571
同じようにもう一つのお店も平均を出します。
list_mogupotates = [4.5,3.8,5.8,5.4,6.4,\
4.2,3.0,4.6,5.8,5.2,\
3.9,3.2,4.0,5.9,3.3,\
6.6,4.9,2.2,3.2,6.4,\
0.8,7.6,7.7,5.1,6.4,\
5.6,3.3,3.9,3.1,2.6,\
3.2,7.0,6.7,6.1,2.6,\
6.9,3.7,3.3,4.6,5.2,\
4.4,3.0,7.5,2.2,5.8,\
4.7,4.1,2.7,4.0 ]
array_mogupotates = np.array(list_mogupotates)
sp.mean(array_mogupotates)
4.614
そんなに平均に差が出ないのに、見た目が随分違うので、ヒストグラムで確かめて見ます。
sns.distplot(array_wakupotates,bins = 8,color = 'blue',kde = False)
sns.distplot(array_mogupotates,bins = 8,color = 'red',kde = False)
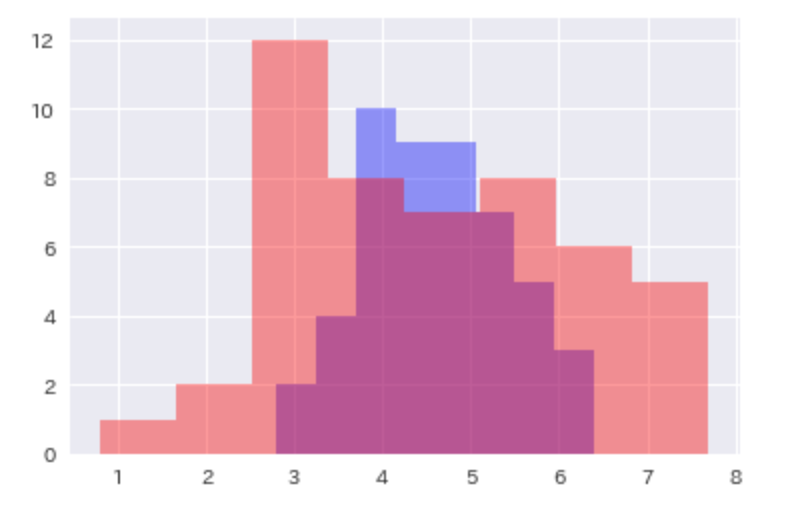
wakupotates(青)は真ん中に集中しているの対して、
mogupotates(赤)は広い範囲で分布していそうということがわかりました。
それではこのバラツキを計算してみます。言わずもがな分散(標本分散)です。
分散 = \frac{(各データ-平均)の総和}{サンプルサイズ}\\
標準偏差 = \sqrt{分散}
sigma_2_waku = sp.sum((array_wakupotates-mu)**2)/N
sigma_waku = sp.sqrt(sigma_2_waku)
print("分散:"+str(sigma_2_waku))
print("標準偏差:"+str(sigma_waku))
分散:0.6808163265306122
標準偏差:0.8251159473253514
これも一発で出ますね。
sp.var(array_wakupotates,ddof=0)
0.681
sp.std(array_wakupotates,ddof=0)
0.825
mogupotatesも調べておきます。
sp.var(array_mogupotates,ddof=0)
2.585
sp.std(array_mogupotates,ddof=0)
1.608
平均は同じようなものでも、mogupotatesの方が分散(標本分散)も標準偏差も大きいことがわかりました。
※ここまで分散は標本分散を使っていましたが、実際には過小評価されることを加味して不偏分散を使います。
不偏分散 = \frac{(各データ-平均)の総和}{サンプルサイズ−1}\\
標準偏差 = \sqrt{分散}
sigma_2_waku = sp.sum((array_wakupotates-mu)**2)/N-1
sigma_waku = sp.sqrt(sigma_2_waku)
print("分散:"+str(sigma_2_waku))
print("標準偏差:"+str(sigma_waku))
分散:0.695
標準偏差:0.8336666000266533
sp.var(array_wakupotates,ddof=1)
0.695
sp.std(array_wakupotates,ddof=1)
0.834
sp.var(array_mogupotates,ddof=1)
2.639
sp.std(array_mogupotates,ddof=1)
1.624
信頼区間
ポテトの本数が気になるというお客さんがきます。他のポテトと比べて多いのか少ないのか。
こういう時はランダムサンプリングをして母集団の推定を行います。
標本平均の平均は母平均と等しくなるという性質を使います。先ほどの不偏分散はここで出てきます。
この際、サンプルサイズが多ければ、標本平均と母平均が近くなります。どういうことか。
**標本平均の分散(バラツキ)は、母分散(不偏分散)をサンプルサイズで割ったものになります。**つまりサンプルサイズが多ければ割る数も大きなるので、標本平均の分散も小さくなるということです。(=>いくつか完成したポテトを選んで、各ポテトに入っている本数がどれくらいばらついているかは、母分散をサンプルサイズで割ったもの)
ということは、標本平均がどれくらいの範囲にバラつくかが分かれば、自然と母平均もその範囲に入るということになります。
ここで使うのは標本平均の標準偏差、つまり標準誤差です。
標準誤差 = \sqrt{{不偏分散}\div{サンプルサイズ}} \\
標準偏差 = \sqrt{分散}
計算してみます。
list_wakupotates_cnt=[47,51,49,50,49,46,51,48,52,49]
array_wakupotates_cnt = np.array(list_wakupotates_cnt)
N = len(array_wakupotates_cnt)
mu = sp.mean(array_wakupotates_cnt )
var = sp.var(array_wakupotates_cnt ,ddof = 1)
準備が終わったらt分布(自由度はサンプルサイズ−1)にしたがって計算を行います。
信頼区間 = 標本平均 \pm{t}\times{標準誤差} \\
信頼区間 = 標本平均 \pm{t}\times{\sqrt{不偏分散\divサンプルサイズ}}
信頼区間95%と99%どちらも計算します。
stder = sp.sqrt(var/N)
max_kukan95 = mu+2.262*stder
min_kukan95 = mu-2.262*stder
print("95%信頼区間:"+str(min_kukan95)+"~"+str(max_kukan95))
stder = sp.sqrt(var/N)
max_kukan99 = mu+3.250*stder
min_kukan99 = mu-3.250*stder
print("99%信頼区間:"+str(min_kukan99)+"~"+str(max_kukan99))
95%信頼区間:47.85966028186881~50.54033971813119
99%信頼区間:47.27422454291496~51.12577545708505
※結果は一緒ですが、標準誤差について
・$σ\div{\sqrt(N)}$:標準偏差をNの平方根で割る
・$\sqrt{σ^2\div{N}}$:不偏分散をNで割ったものの平方根
があります。どちらも一緒です。
さて、これらの信頼区間も一瞬で出ます。
stats.t.interval(alpha = 0.95,df = N-1,loc = mu,scale = stder)
(47.860, 50.540)
stats.t.interval(alpha = 0.99,df = N-1,loc = mu,scale = stder)
(47.274, 51.126)
終わり
楽勝ですね。続きはこちら