この記事は古川研究室 古川研究室Advent_calender9日目の記事です。
本記事は古川研究室の学生が学習の一環として書いたものです。内容が曖昧であったり表現が多少異なったりする場合があります。
情報量
まず情報量について、例えば、犬が人をかんでもそれほど驚きませんが、人が犬をかんだらとても驚きますよね！これは、（生起確率）発生確率が小さいことが発生したときの方が、情報量(ここでは驚き度)が大きいことを意味しています。だから、生起確率が小さくなるにつれて、情報量は次第に多きくなることがわかります。したがって、以下の式で表されます。
ビットのとき
$$ I = -log_2P$$
ナットのとき
$$ I = -log_eP$$
ビット(bit)はbinary unitの略、ナット(nat)はnatural unitの略で、単位の違いだけですが、微分の計算の時はナットが便利です。
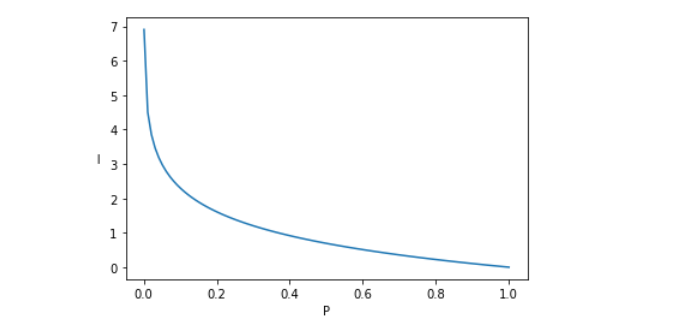
横軸に確率$P$縦軸に情報量$I=-logP$をプロットした図です。確率値が高くなればなるほど、情報量が少なくなることがわかります。
#エントロピー
エントロピーは情報源の平均情報量であり、情報源全体としてどのくらい情報量を持っているかを表します。
$$ H(s) = -\sum_{i=1}^Mp_ilog_2p_i$$
エントロピーの意味
明日の天気を予測する場合、情報源のA子さんは事象晴れ、雨、曇りがそれぞれ同じ確率で発生すると予測するとします。
晴れ：確率$1/3$
雨：確率$1/3$
曇り：確率$1/3$
プロの気象予報士B子さんは以下のように予測するとします。
晴れ：確率$4/5$
雨：確率$1/10$
曇り：確率$1/10$
このときの、エントロピー(平均情報量)を計算します。
A子さん:$H(A)=-\frac{1}{3}log_2\frac{1}{3}-\frac{1}{3}log_2\frac{1}{3}-\frac{1}{3}log_2\frac{1}{3}=1.585$
B子さん：$H(A)=-\frac{4}{5}log_2\frac{4}{5}-\frac{1}{10}log_2\frac{1}{10}-\frac{1}{10}log_2\frac{1}{10}=0.922$
エントロピーは__情報源のあいまいさ__を表しています。値が大きいほどあいまいであり、小さいほどあいまでないことを表します。
上の場合は、天気予報のあいまいさを表しており、A子さんはそれぞれ晴れ、雨、曇りが同じ確率で発生すると予測、すなわち明日の天気の予測ができていない状況であるため、エントロピー（あいまいさ）が大きく、B子さんはおおよそ晴れであると予測しているため、エントロピーが小さくなっています。
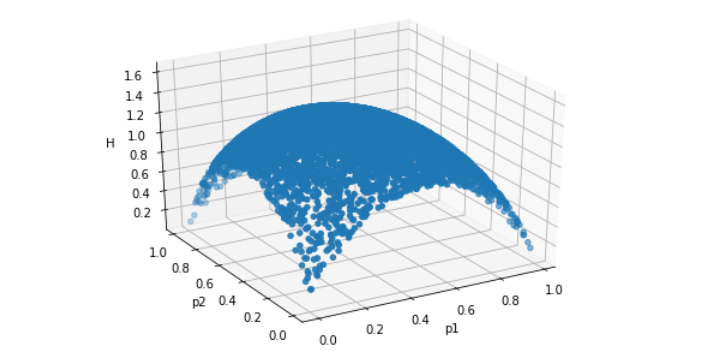
上の3元情報源を一般化します。
事象$a_1:p_1$
事象$a_2:p_2$
事象$a_3:1-p_1-p_2$
プロットするとこんな感じです。
分かりにくいですが、$p_1=p_2=1/3$で最大値をとっており、また、生起確率$p_1,p_2$が$0$もしくは$1$のとき、すなわち事前にどれが発生するかわかっているとき、エントロピーは$0$（あまいさがゼロ）になります。
#結合エントロピー
事象$x_i$および事象$y_i$の生起確率をそれぞれ$P(x_i)${$i=1,...,M$}および
$P(y_i)${$j=1,...,N$}で表すとし、それぞれの情報源$X,Y$とすると、結合エントロピーは以下で与えられます。
$$
H(X,Y)=-\sum_{i=1}^M\sum_{j=1}^NP(x_i,y_j)log_2P(x_i,y_j)
$$
このエントロピーは$X$と$Y$の値を同時に知った時に得られる平均情報量(あいまいさ)です。先ほどの、エントロピーの多変量化と捉えることができます。
#条件付きエントロピー
情報源$Y$が知られた場合の情報源$X$のあいまいさ$H(X|Y)$は以下で与えられます。
$$
H(X|Y)=-\sum_{i=1}^M\sum_{j=1}^NP(y_j)P(x_i|y_j)log_2P(x_i|y_i)
$$
同様に、情報源$X$が知られた場合の情報源$Y$のあいまいさ$H(Y|X)$は以下で与えられます。
$$
H(Y|X)=-\sum_{i=1}^M\sum_{j=1}^NP(x_i)P(y_j|x_i)log_2P(y_j|x_i)
$$
意味から考えて、情報源$Y$の値を得た後の情報源$X$のあいまいさ$H(X|Y)$は、情報源$X$のあいまいさ$H(X)$以下になります。情報源$Y$に関しても同様です。
#相互情報量
上記の条件付きエントロピーにおいて、$H(X|Y)≦H(X)$、$H(Y|X)≦H(Y)$となっていることを示しました。
情報源$X$と$Y$が互いに関連がある場合、一方の情報源から他方の情報源についてある情報源が間接的に得られたのです。これを定量的に示したのが相互情報量です。相互情報量は次式で示されます。
$I(X;Y)=H(X)-H(X|Y)$
または
$I(X;Y)=H(Y)-H(Y|X)$
図で示すとわかりやすいです。
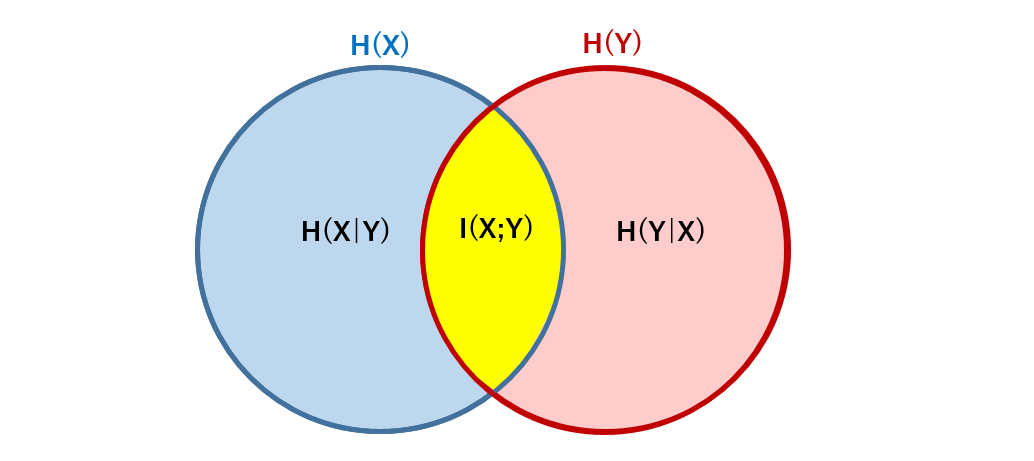
この図より、情報源$X$と情報源$Y$が互いに独立であるときは、$H(X|Y)=H(X)$、$H(Y|X)=H(Y)$となり、相互情報量$I(X;Y)$は$0$になることが分かります。また、情報源$X$と情報源$Y$の関連度が高ければ高いほど、図で示すところの黄色の部分が多くなり、相互情報量も大きくなることが分かります。
相互情報量は情報源$X$と情報源$Y$の関連の度合いというイメージですね。
#おわりに
今回、情報量からエントロピー、相互情報量までざっとまとめました。
この記事が誰かのお役に立つと幸いです。
#参考文献
https://www.coronasha.co.jp/np/isbn/9784339012026/