前回まで
前回は、単純に9984(ソフトバンク)の株価を表示してみました。
今回は、その株価の移動平均を計算してみます。
移動平均とは
移動平均にも様々な種類がありますが、単純移動平均の場合は、$p_t$を$t$日前の価格とすると、n日移動平均は、過去n日間の終値の平均値になります。
$$SMA_t = \frac{p_t + p_{t-1} + \ldots + p_{t - \left( n - 1 \right)}}{n};t \geq n - 1$$
移動平均は株価のテクニカル分析においてもっとも基本的な指標のひとつで、ゴールデンクロスやデッドクロスという条件の判定に用いられます。ゴールデンクロスは、5日移動平均線が25日移動平均線を上回ったときに「買うといいよ」ということで、デッドクロスはその反対です。
今回は、株価調整後の終値で移動平均を計算してみます。
コード
いきなりですが、コードです。
def _mavg_signal(data):
m5 = data["close_price_adj"].fillna(method='ffill').rolling(window=5, center=False).mean()
m25 = data["close_price_adj"].fillna(method='ffill').rolling(window=25, center=False).mean()
return {
"mavg_5:price": m5,
"mavg_25:price": m25,
}
# シグナル登録
ctx.regist_signal("mavg_signal", _mavg_signal)
initialize()の中で、_mavg_signal という関数を、ctx.regist_signal()で登録します。
_mavg_signal()の中では、5日移動平均と25日移動平均の2種類計算しています。
パラメータであるdataは、pandas.Panel型になり、3次元構造をとります。その3次元構造というのは、
axis-0(items): データ項目(close_price, volume, etc.)
axis-1(major): 日付(datetime.datetime型)
axis-2(minor): 銘柄名(symbol object型)
https://quantx.io/handbook/ja/#initialize より引用
というような構造になっているようです。なかなか想像しにくいですが、Excelみたいに考えるとわかりやすいかもしれません("行,列,シート"で3次元?)
handbookに実際の内部イメージが書かれていますが、axis-0のデータ項目を決めてやって2次元に落としてから、pandas.DataFrameの機能で移動平均を計算し、戻り値としてdictの値として返しています。
実行してみる
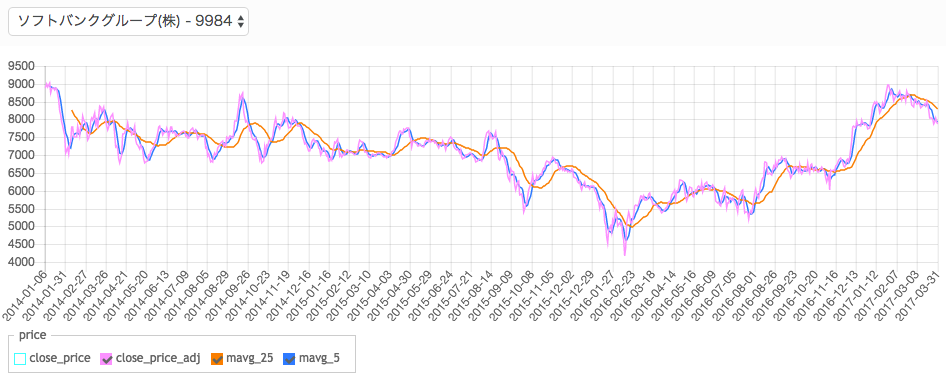
出てきました!
mavg_5というのが5日移動平均で、mavg_25が25日移動平均です。5日移動平均は、終値(close_price_adj)とあまり変わらないので、見にくいですね。
本当に計算できてる?
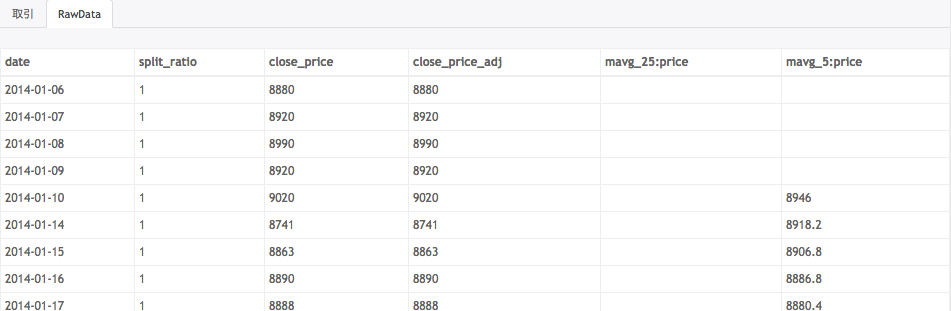
本当に計算できているのかな、ということでチャートのしたのRawDataというタブで、実際の計算結果を確認してみます。
2014-01-10の5日移動平均の値は、$\frac{8880 + 8920 + 8990 + 8920 + 9020}5 = 8946$ ということで、計算できているっぽいですね! mavg_5:priceは5日移動平均なので、バックテストを開始してから4日目までは計算できないので空欄になっています。
チャートの軸
移動平均を計算する_mavg_signal()では、
return {
"mavg_5:price": m5,
"mavg_25:price": m25,
}
というdictを返しました。dictの値は移動平均の計算結果のpandas.DataFrameです。
keyはチャートの軸名になりますが、:priceというのがポイントになっていて、チャートにおけるスケールを指定しています。
:priceというのは、あらかじめ定義されているスケールで、該当銘柄の株価スケールになります。mavg_5とmavg_25の軸を同じにすることで、はじめてチャート上で比較することが可能になります。
ためしに、
return {
"mavg_5:mavg_5": m5,
"mavg_25:mavg_25": m25,
}
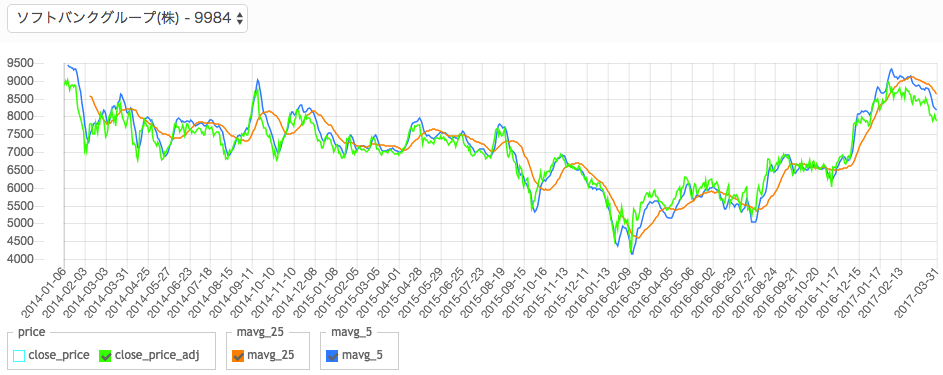
という感じで、実行してみると、
それぞれの移動平均値の縦軸のスケールが異なるため、微妙にチャートの重なり具合が変わってきています(わかりにくい)
そのため、このチャートからゴールデンクロスやデッドクロスの判断を行うのは難しくなりますので、軸は揃えましょう。
まとめ
今回のコードです。
def initialize(ctx):
ctx.configure(
target="jp.stock.daily",
channels={
"jp.stock": {
"symbols": [ "jp.stock.9984" ],
"columns": [ "close_price_adj" ]
}
}
)
def _mavg_signal(data):
m5 = data["close_price_adj"].fillna(method='ffill').rolling(window=5, center=False).mean()
m25 = data["close_price_adj"].fillna(method='ffill').rolling(window=25, center=False).mean()
return {
"mavg_5:price": m5,
"mavg_25:price": m25,
}
# シグナル登録
ctx.regist_signal("mavg_signal", _mavg_signal)
def handle_signals(ctx, date, current):
'''
current: pd.DataFrame
'''
pass
次回は、もっと複雑な指標を計算して表示してみようと思います。
参考情報
2018/1/11追記 正式版URL: