この記事では、私が最近設立に関わったtensor4allというグループを紹介します。
始めに
計算物理において、多くの重要な問題は数値的に解くのが極めて困難であり、特に量子多体系のシミュレーションや、超伝導体、分子シミュレーション、さらには量子コンピュータの基礎となるナノエレクトロニクスや超低温原子気体といった分野が含まれます。これらの問題に加え、部分微分方程式(PDE)の解法も非常に計算が重い場合があります。
このような多次元の問題を情報圧縮し解く技術として、ニューラルネットワークに代表される機械学習モデルが知られていますが、tensor4allでは特に「テンソルネットワーク」ベースの機械学習アルゴリズムを開発しています。後で解説するように、テンソルネットワークは情報の圧縮能力だけではなく、圧縮したまま演算することに長けています。元々、テンソルネットワークは、量子多体系の波動関数を圧縮するために考案されましたが、徐々にその適用範囲を拡げてきました。特に、応用数学の分野では、テンソルネットワークベースの機械学習アルゴリズムが様々開発されています。それらが物理に再導入される形で、量子多体波動関数以外の対象にも適用範囲を広げています。
一方、ディープニューラルネットワークベースの機械学習モデルの多くは勾配法に最適化を頼っています。一方、tensor4allで開発するアルゴリズムは、LU分解などの基本的な線形代数を利用しており、遅い勾配ベースの最適化とは異なる高速な学習が可能です。
tensor4allは、これらの新しい流れを牽引する物理学者らによって設立されました。CEAグルノーブルのWaintalグループ、LMUミュンヘンのvon Delftグループ、フラットアイアン研究所のParcolletグループ、日本からは私のグループが設立に関わっています。
最近、tensor4allのメンバーが中心になって、テンソルネットワークベースの機械学習アルゴリズムである、Tensor Cross Interpolation (TCI)の高速なアルゴリズムと実装を公開してます。C++, Python, Juliaの実装が公開されていて、量子多体系だけではなく量子情報の分野でも使われています。テンソルネットワークやTCIの基礎数理は、その論文の最初の数章で基本的な内容が十分解説されているため、興味がある方はご覧下さい。
今回の記事では、細かいことはさておき、Juliaでどのような計算が可能なのか例を示してみます。オンラインで公開されているチュートリアル集からの抜粋です。
Quantics Tensor Train (QTT)
その前に、Quantics Tensor Train (QTT)表現を解説しましょう (TCIとは独立の概念です)。
ある関数$f(x)$が与えられているとしましょう ($x \in [0, 1]$)。この関数をテンソルネットワークをつかって情報圧縮するには、まず関数をテンソル (=多次元データ)として表現する必要があります。因みに、TTとは、matrix product stateの応用数学分野の呼称です。コアテンソルが電車の車両のように並んで、連結されているイメージから来てます。話がそれましたが、まず$x = \sigma_1/2 + \sigma_2/2^2 + \cdots \sigma_R/2^R$というように、$R$ビットの2進数を使って、$x$を離散化します。すると、関数は、$F_{\sigma_1 \sigma_2 \cdots \sigma_R} = f(\sigma_1/2 + \sigma_2/2^2 + \cdots \sigma_R/2^R)$と離散化できます。この操作は、$[0, 1)$で$2^R$個の等間隔グリッドを構成して、グリッド上で関数の値をサンプリングすることに対応しています。この段階では、情報は圧縮されていません。
次に、$R$次元データ$F_{\sigma_1 \sigma_2 \cdots \sigma_R}$をTT形式で圧縮します。つまり、
$$
F_{\sigma_1 \sigma_2 \cdots \sigma_R} \approx \mathrm{Tr}[M^1_{\sigma_1} M^2_{\sigma_2} \cdots M^R_{\sigma_R}].
$$
ここで、それぞれの$M$は、3次元のテンソルで大きさは$\chi \times \chi \times 2$ (2は$\sigma$の足)です。ここで、$\chi$が所謂ボンド次元と呼ばれているもので、$\chi$が最悪$2^{R/2}$まで大きくなりますが、それより十分小さくてすめば、指数的にデータを圧縮できます。QTTは多次元関数にも拡張可能ですが、ここでは1変数の場合に留めておきましょう。
どういう関数が圧縮可能でしょうか?一番簡単な例は指数関数$e^{a x} = e^{a \sigma_1/2} \cdots e^{a \sigma_R/2^R}$で、QTTではボンド次元$\chi=1$の表現を持ちます。他には、多項式もQTT圧縮可能ですし、いろんな例が知られています。
重要な点は、$\chi$が小さくすめば (関数がQTT表現で低ランク)、データ量は高々$R$に比例する一方、グリッドの解像度を$R$に対して指数的に細かく出来ることです!これにより、桁違いに違う長さスケールが共存している関数を圧縮できる可能性があります。
ここまで読むと、QTTを持ち出さなくても、ディープニューラルネットワークなどでも圧縮できるのでは?と思い当たる人もいるかも知れません。QTTのメリットは、圧縮したまま、積分や、フーリエ変換、畳み込み積分など、基本的な数学的な演算が可能な点です。ニューラルネットワークの場合、積分は一般的にモンテカルロ積分が必要なのですが、QTTでは、
$$
\int dx f(x) \approx \frac{1}{2^R} \sum_{\sigma_1 \cdots \sigma_R} F_{\sigma_1 \cdots \sigma_R} = \frac{1}{2^R} \mathrm{Tr}[(\sum_{\sigma_1} M^1_{\sigma_1}) ((\sum_{\sigma_2} M^2_{\sigma_2}) \cdots (\sum_{\sigma_R} M^R_{\sigma_R})].
$$
という感じに、それぞれのテンソルの和を取った後に、積を計算する簡単な演算になります。
Tensor Cross Interpolation (TCI)
非常に駆け足ですが、上では、関数をどうやってテンソル化して圧縮するかを見てきました。
では、物理に出てくるような複雑な関数やデータを圧縮できるか、どうやって判定するのでしょうか?
数値データは非常に細かいグリッド上で定義されていて、数TBあるかもしれません。もしくは、与えられた$(\sigma_1 \cdots \sigma_R)$に対して複雑な計算をして値を返す「関数」として定義されているかも知れません。このような場合、$F_{\sigma_1 \cdots \sigma_R}$の数値データを特異値分解で分解して、TT表現を求めることは現実的ではありません。
Tensor Cross Interpolationは応用数学の分野で開発された、特異値分解とは別のアプローチで、元のテンソルのデータを全部読まずにTTを構成することを可能にします。ここで詳しい数学の話はしませんが、TCIとは以下の様な性質を持つアルゴリズムです。TCIは、与えられた関数が任意の点で評価可能であること仮定しています。これを使って、TCIは動的にサンプリング点を選んで関数を評価します。その結果を基に高速にTT表現を構築します。実際には、TT表現の精度をその都度評価して、近似精度が足りない部分に動的にサンプリング点を追加しつつ、最適な$\chi$を決定していきます (興味のある方は是非論文を!)関数の性質が良い場合、関数の回数 (サンプリング点)は、$O(\chi^2 R)$程度です。つまり、TTに含まれるパラメータ数程度です。
Juliaの実行例
Pluto.jlによるチュートリアル集があるので、詳しいところはそちらをご覧下さい。Pluto.jlによるウェブサイト構築には、Satoshi Terasakiさんが尽力されました。ローカルでのノートブック実行法は、ここに解説があります。
今回は、最も簡単な例を紹介しましょう。基本的には、Pluto.jlがインストールされていれば、各ページの上に表示されているコマンドを使えばローカルで開けます。今回の例では、以下で動くと思いますが、最新の情報はウェブサイトを参照して下さい。
BASE_URL = "https://raw.githubusercontent.com/tensor4all/T4APlutoExamples/refs/heads/main/pluto_notebooks/"
notebook = "quantics1d.jl"
url = joinpath(BASE_URL, notebook)
using Pluto; Pluto.run(notebook=download(url))
この例は Ritter2024 の図1から引用されて、以下の関数の積分
$$
\mathrm{I}[f] = \int_0^{\ln 20} \mathrm{d}x , f(x)
$$
を計算します。
$$
f(x) = \cos\left(\frac{x}{B}\right) \cos\left(\frac{x}{4\sqrt{5}B}\right) e^{-x^2} + 2e^{-x},
$$
ここで、$ B = 2^{-30} $ です。 この積分の結果は次のようになります:
$$
\mathrm{I}[f] = \frac{19}{10} + O(e^{-1/(4B^2)}).
$$
関数の解析を見れば分かるとおり、速い振動 ($B$程度の間隔)と遅い減衰が共存する複雑な形状をしています。ただ、TCIを使えば、このQTT表現を、関数のサンプリング結果から構築することが出来ます。
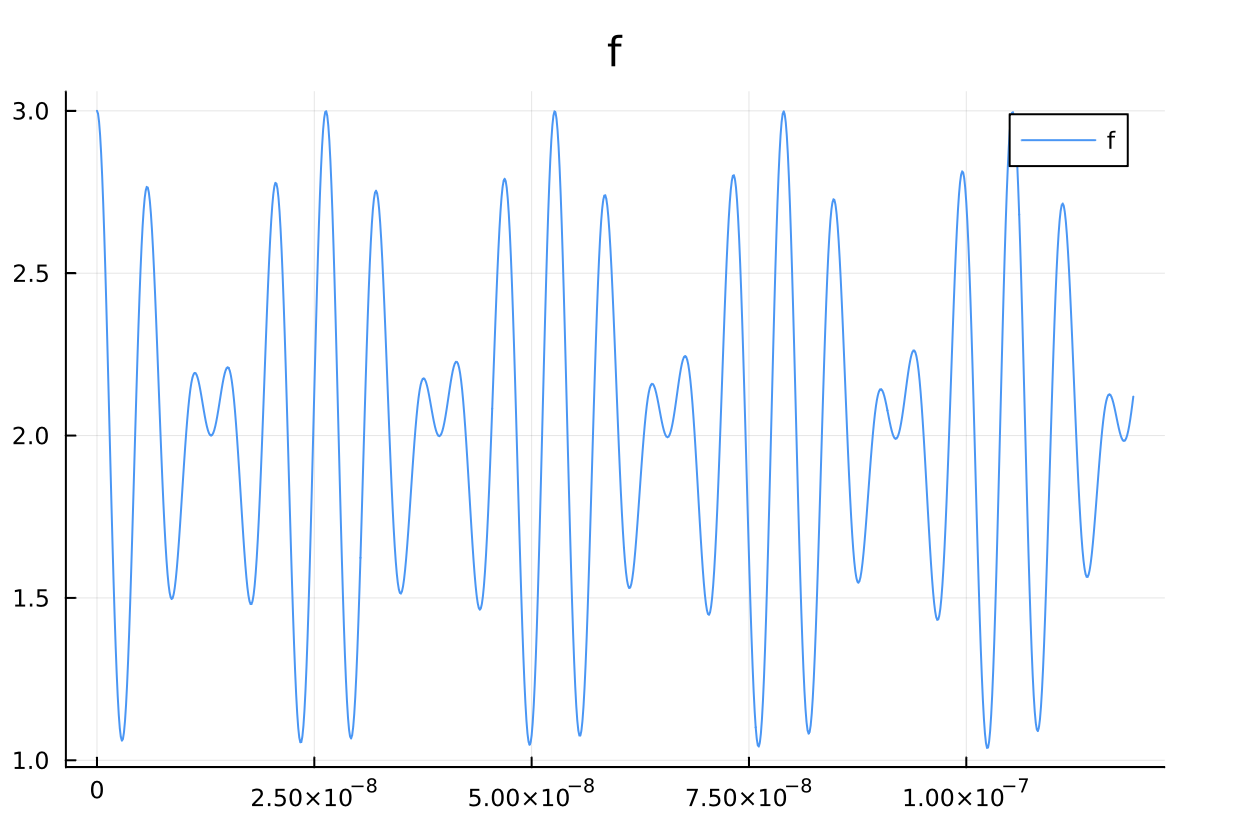
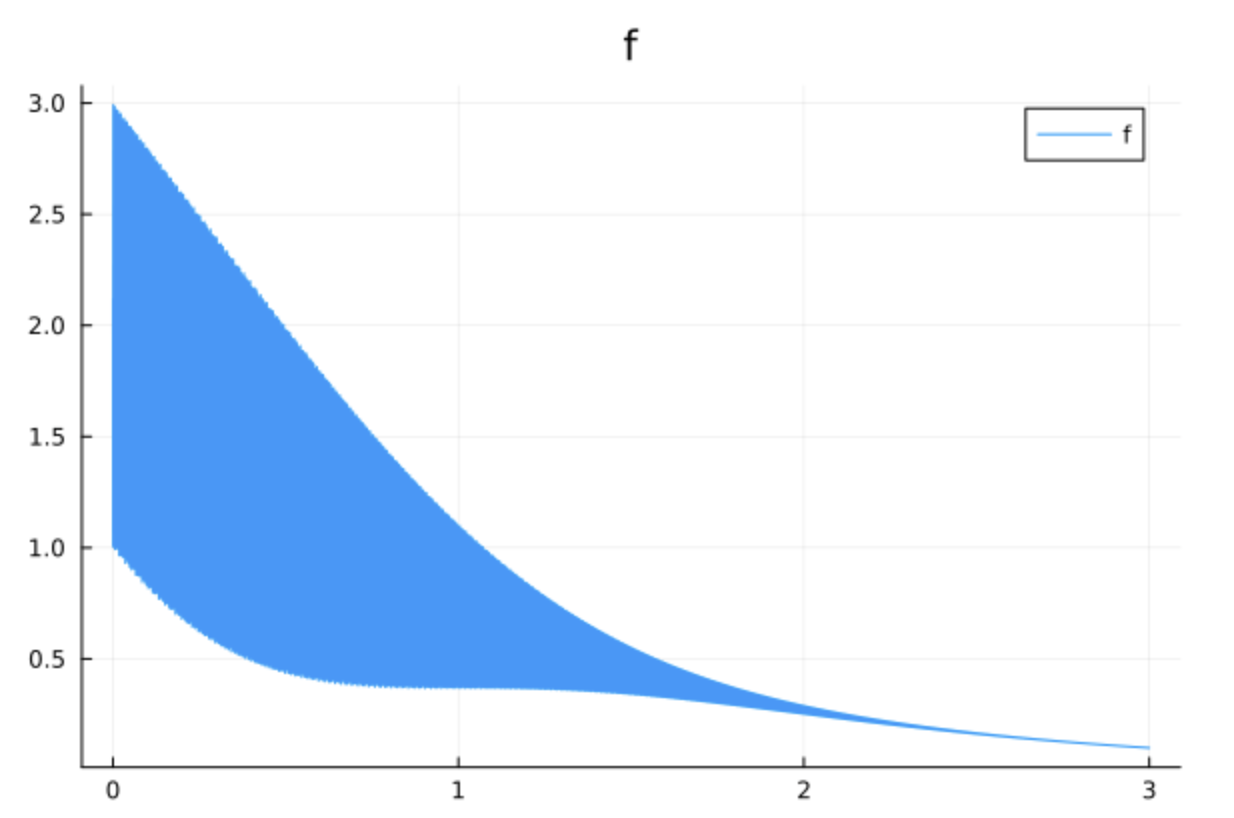
実際のコードは少し長いので、チュートリアル集から、結果をだけ抜粋します。
ちなみに、本当に重要な部分のコードは、以下の一行で、quanticscrossinterpolate関数に、対象の関数fを渡しているだけです。
ci, ranks, errors = quanticscrossinterpolate(Float64, f, qgrid; maxbonddim = 15)
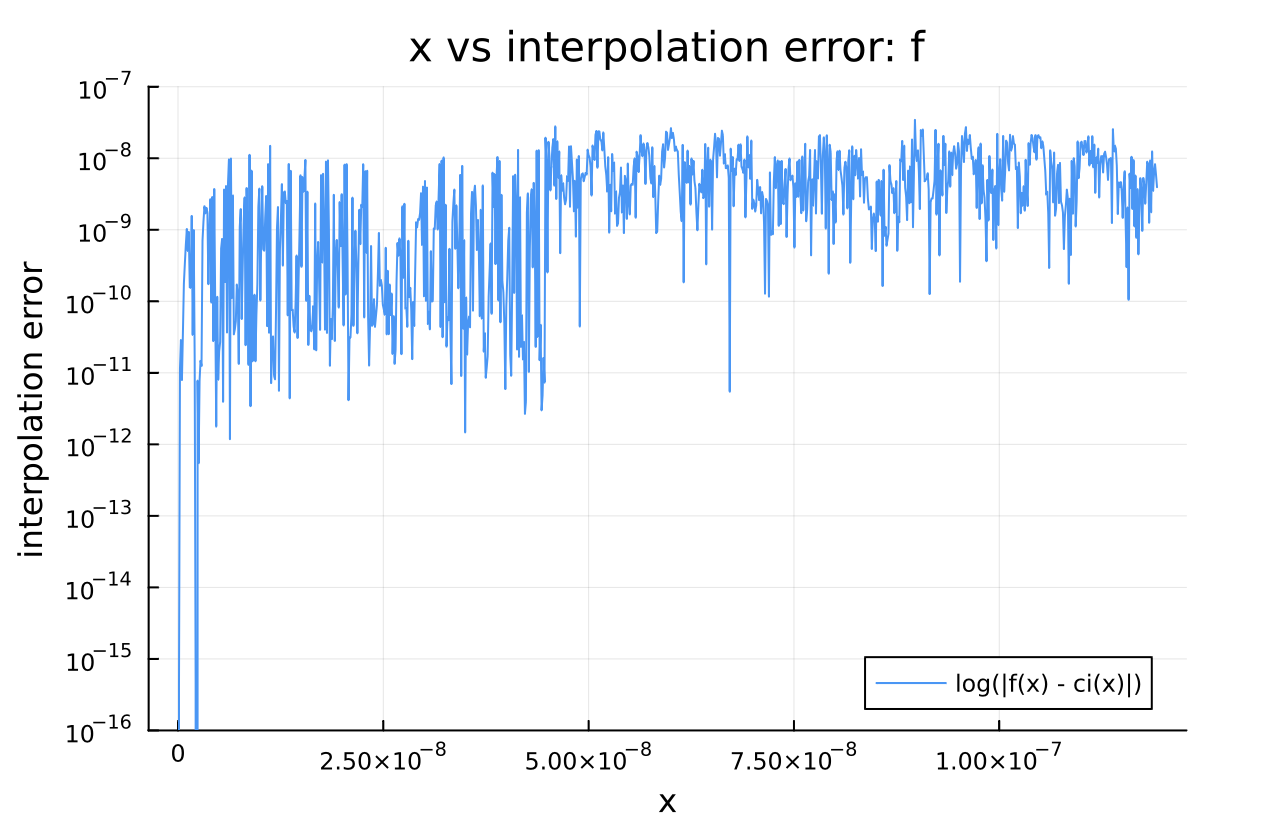
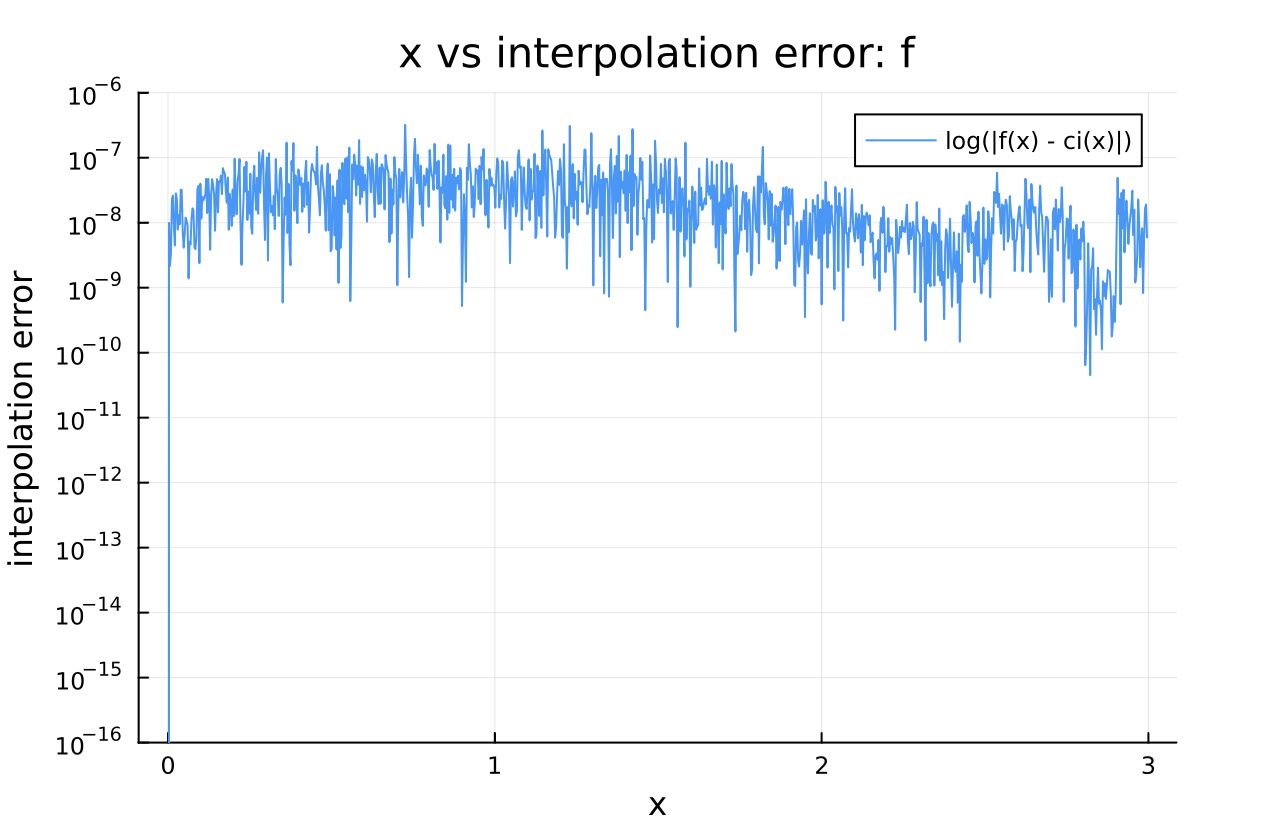
ボンド次元15ぐらいの内挿結果は、以下の様になって、すべての$x$の範囲で極めて高精度に近似されていることが分かります。
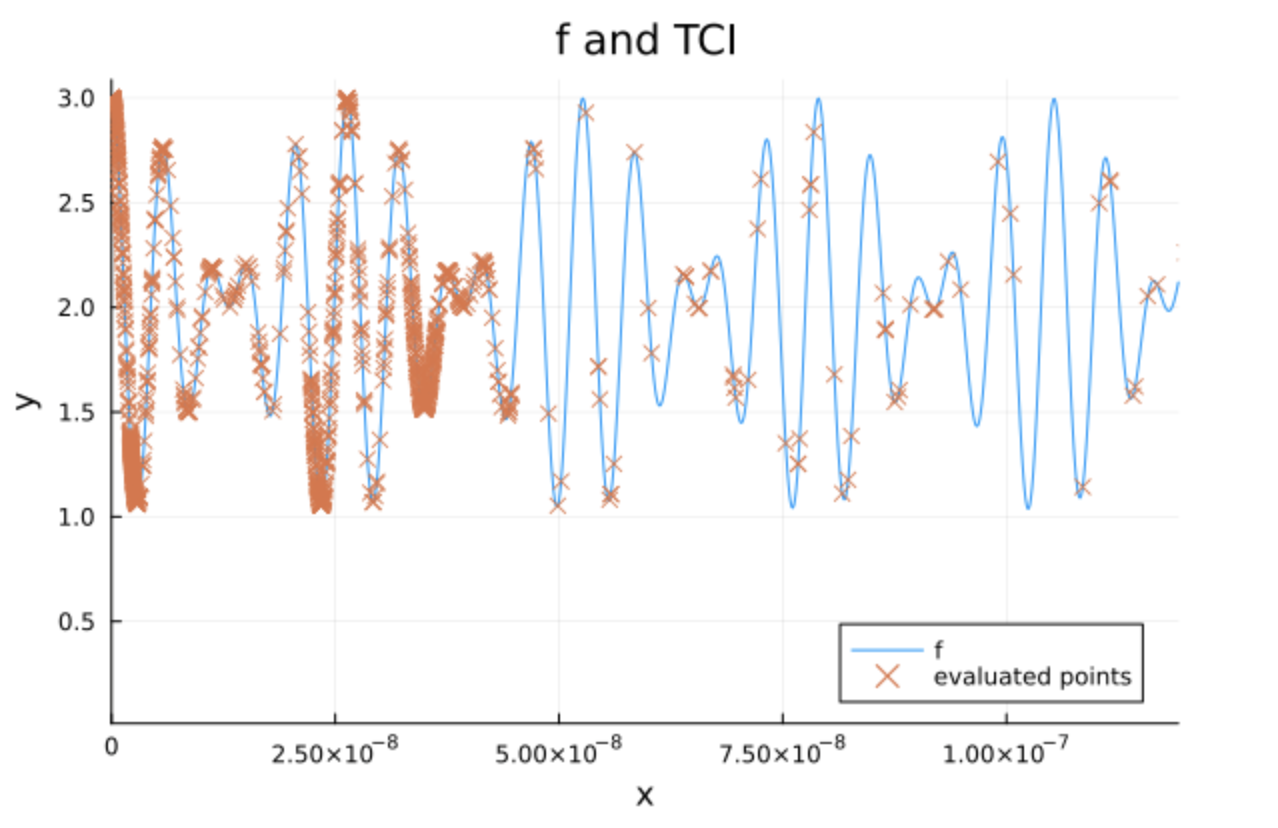
なお、サンプリング点は、こんな感じに重要な部分が自動的に選ばれていることが分かります。
まとめ
以上では、簡単な例しか示しませんでしたが、高次元関数の近似、積分やフーリエ変換などの例はチュートリアル集に用意されています。また、TCIの結果得られるTTは、ITensors.jlのMPSオブジェクトに変換することも出来ます。