LoginSignup
0
0

More than 3 years have passed since last update.

@hironarin

TeX&TikZで低気圧モデル（回転系の運動）

Last updated at Posted at 2021-02-06

$$
\def\fraction(#1/#2){\frac{#1}{#2}}\def\ff(#1/#2){\frac{#1}{#2}}\def\der(#1/#2){\frac{d #1}{d #2}}\def\dd(#1/#2){\frac{d #1}{d #2}}\def\del{\partial}\def\pdd(#1/#2){\frac{\del #1}{\del #2}}\def\DIS{\displaystyle}\def\Dt{\Delta t}\def\bm{\boldsymbol}
$$

TeXマクロ終了

はじめに

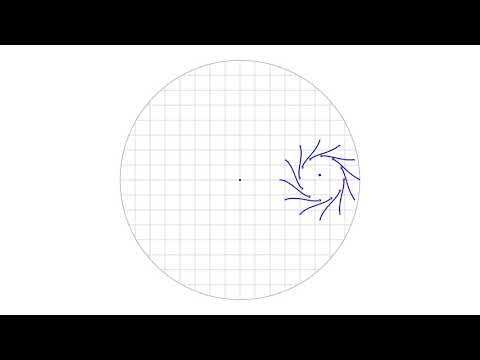
地球上の低気圧は，北半球では反時計回りに，南半球では時計回りに回転しながら中心部に空気を吸い込みます。回転の方向の原因は主に地球の自転による「コリオリ力」だと言われています。「ホントかよっ！」って思うので，TeXとTikZで作ってみました。

https://youtu.be/XTB3nxHq0LM
IMAGE ALT TEXT HERE

https://youtu.be/lYW5mVQ_Y90
IMAGE ALT TEXT HERE

主は，プログラミングの素人なので，作りはかなり幼いよう見えると思います。

TeXの計算能力は決して高くないので，計算の精度や作れる動画の尺には限界があります。

運動方程式を解くためのルンゲクッタ

運動方程式は

$$
\DIS \fraction(d^2x/dt^2) = f(x)
$$

を扱います。右辺の$f$は力を質点の質量で割ったものです。微分方程式を

\fraction(dv/dt) = f(x) \cdots (1)
\\
\fraction(dx/dt) = v(t) \cdots (2)

と2つの方程式にして取り扱います。(2)を積分すると，

x (t_0 + \Delta t) = x_0 + v_h \cdot \Delta t
\\
v_h = v(t_0 + \fraction(1/2)\Delta t )

積分値$x(t_0 + \Delta t)$を得るために，半分のステップ進んだ速さ$\DIS v(t_0 + \fraction(1/2)\Delta t )$の値が必要になります。(1)式を1ステップだけ積分した値は次のようになります。$v_0=v(t_0)$，

$$
v (t_0 + \Delta t) = v_0 + \phi \Delta t
$$

$$
\phi = f(x_0 + v_0 \cdot \fraction(1/2)\Delta t)
$$

この式に$\Delta t /2$を代入したものが$v_h$です。

$$
\DIS
v_h = v_0 + \phi \cdot \ff(\Delta t /2)
$$

$$
\phi = f(x_0 + v_0 \cdot \fraction(1/4)\Delta t)
$$

手順をまとめると次のになります。

  1. $v(t_0 + \Delta t)$を得る ・・・・・・次の$v_0$になる

    1. $f$に$t + \Delta t/2$，$x_0$，$v_0$を代入する

  2. $v_h = v(t_0 + \Delta t/2)$を得る ・・・・・・$x(t_0+\Delta t)$を得るため

    1. $f$に$t + \Delta t/4$，$x_0$，$v_0$を代入する

  3. $x(t_0+\Delta t)$を得る・・・・・・次の$x_0$になる。

回転系の運動

回転系の運動方程式(コリオリ力・遠心力)

慣性系に対して，一定の角速度で回転して観測をしている系を考えます。例えば自転をしている地球上で観測した物体の運動など。

$$
m \dd(^2/t^2) \bm x = \bm F + 2m\bm \omega \times \bm v + m \bm \omega \times (\bm \omega \times \bm x)
$$

注意するべきは，回転系で観測した位置座標・速度を使う点です。力$\bm F$は慣性系で働く力をそのまま使います。

以下では，質量で割った，

$$
\dd(^2/t^2) \bm x = \bm f + 2\bm \omega \times \bm v + \bm \omega \times (\bm \omega \times \bm x)
$$

の形で話を進めます。

TeX&TikZ コード

変数の名前は，紆余曲折を経て，変な名前になりました。笑ってあげましょう。

力・加速度関数

以下の形の，4変数の関数の形で定義します。関数の定義の仕方は，TeXでマクロを作る方法と同じです。

\def\funcAccelX#1#2#3#4{
2*\freq * (#4) + 0*\freq * \freq * (#1) - \freqP * \freqP * (#1) 
+ \PForce * (#1 - \variXCdMonkey)/sqrt((\variXCdMonkey -#1)^2 + (\variYCdMonkey -#2) ^2)^1  - \vFrac * (#3)
}
\def\funcAccelY#1#2#3#4{
-2*\freq * (#3) + 0*\freq * \freq * (#2) - \freqP * \freqP * (#2) 
+ \PForce * (#2 - \variYCdMonkey)/sqrt((\variXCdMonkey -#1)^2 + (\variYCdMonkey -#2) ^2)^1 - \vFrac * (#4)
}
% #1#2 テスト粒子のx,y座標 #3#4 テスト粒子の速度x,y成分

ルンゲクッタコード

ここは，実際にループして計算を行うブロックになります。

①初期値入力 → ②ルンゲクッタ計算 → ③値を出力

初期値の代入

繰り返し（ループ）を用いて計算するため，ステップごとに逐次値を代入していく。

\tikzmath{
    \NqtXTako = \csname variXCdNuko[\z] \endcsname;
    \NqtYTako = \csname variYCdNuko[\z] \endcsname;
    \NvtXTako = \csname variXVelocityNuko[\z] \endcsname;
    \NvtYTako = \csname variYVelocityNuko[\z] \endcsname;
}
計算部分

基本パーツは次の3つ

$\Delta t /2$(半ステップ)あとの速度

$\Delta t$(1ステップ)あとの速度（次のステップの初期値）

$\Delta t$(1ステップ)あとの位置座標

\tikzmath{
%半ステップ速度
    real \variFuji;
    \variFuji1=\NqtXTako;
    \variFuji2=\NqtYTako;
    \variFuji3=\NvtXTako;
    \variFuji4=\NvtYTako;
    \NatXTako = \funcAccelX{\variFuji1}{\variFuji2}{\variFuji3}{\variFuji4};
    \NatYTako = \funcAccelY{\variFuji1}{\variFuji2}{\variFuji3}{\variFuji4};
    %
    \variFuji1=\NqtXTako + 0.25 * \NvtXTako *\dT /\stepC;
    \variFuji2=\NqtYTako + 0.25 * \NvtYTako *\dT /\stepC;
    \variFuji3=\NvtXTako + 0.25 * \NatXTako * \dT /\stepC;
    \variFuji4=\NvtYTako + 0.25 * \NatYTako * \dT /\stepC;
    \NatXTako = \funcAccelX{\variFuji1}{\variFuji2}{\variFuji3}{\variFuji4};
    \NatYTako = \funcAccelY{\variFuji1}{\variFuji2}{\variFuji3}{\variFuji4};
    %
    \NvthXTako = \NvtXTako + 0.5 * \dT / \stepC * \NatXTako;
    \NvthYTako = \NvtYTako + 0.5 * \dT / \stepC * \NatYTako;
    %
    %
%%1ステップのvを計算するよ
            \variFuji1=\NqtXTako;
            \variFuji2=\NqtYTako;
            \variFuji3=\NvtXTako;
            \variFuji4=\NvtYTako;
            \NatXTako = \funcAccelX{\variFuji1}{\variFuji2}{\variFuji3}{\variFuji4};
            \NatYTako = \funcAccelY{\variFuji1}{\variFuji2}{\variFuji3}{\variFuji4};
%
            \variFuji1=\NqtXTako + 0.5 * \NvtXTako *\dT /\stepC;
            \variFuji2=\NqtYTako + 0.5 * \NvtYTako *\dT /\stepC;
            \variFuji3=\NvtXTako + 0.5 * \NatXTako * \dT /\stepC;
            \variFuji4=\NvtYTako + 0.5 * \NatYTako * \dT /\stepC;
%%
            \NatXTako = \funcAccelX{\variFuji1}{\variFuji2}{\variFuji3}{\variFuji4};
            \NatYTako = \funcAccelY{\variFuji1}{\variFuji2}{\variFuji3}{\variFuji4};
%%
            \NvtXTako = \NvtXTako +  \dT / \stepC * \NatXTako;
            \NvtYTako = \NvtYTako +  \dT / \stepC * \NatYTako;
%1ステップ後の座標の計算をするよ。
            \NqtXTako = \NqtXTako + \NvthXTako * \dT / \stepC;
            \NqtYTako = \NqtYTako + \NvthYTako * \dT / \stepC;
}
結果の出力
    \global\expandafter\edef\csname variXCdNuko[\z] \endcsname{\NqtXTako}
    \global\expandafter\edef\csname variYCdNuko[\z] \endcsname{\NqtYTako}
    \global\expandafter\edef\csname variXVelocityNuko[\z] \endcsname{\NvtXTako}
    \global\expandafter\edef\csname variYVelocityNuko[\z] \endcsname{\NvtYTako}

いくつかの注意点

\tikzmathによる計算結果は\loop内でのみ有効で，\loopの外にでると忘れてしまいます（多分ローカル変数）。\loop脱出後も数値を維持しておくために\global\edefを用いる。

\global全体で有効なマクロを作ることができる

\edef数値をとるマクロの作成

変数を配列的に使いたい場合（多粒子系のように），\csnameを使ったトークンを定義する。

\variable → \csname variable \endcsname

\csnameと\endcsnameで挟んで使う。注意すべき点 スペースもトークンを表している文字と認識されるため，スペースを入れている場合は注意を払う

\expandafter

マクロを定義するとき，\defはトークンにバックスラッシュ\を使用することができない。例えば\zの部分は1,2,3,..という数値(実数か整数かは注意)で定義したい場合に困ってしまう。そこで\zに先に数値(数字)であることを認識させるために\expandafterをつけておく。

ループする方法

くり返し計算(ループ)のコードには，LaTeXのカウンターを使用します。実は詳しくは分からないため，コードだけ書きます。コードは2つのブロックからなります。

カウンターの定義

\newcount\countA%ループ用カウンターを定義

ループ部分

\countA = 0 \loop\ifnum\countA < \stepA%ループ開始
{




}
\advance\countA by1\repeat % ループ終了

空行を入れても大丈夫

{ }は書かなくてもいいが，ループを入れ子にする場合，必要になる。何よりあった方が分かりやすい。

'\countA = 0 \loop\ifnum\countA < 10'と書くことで，\loop内を10回繰り返し実行します。

上の例では，\stepAには繰り返しの回数を前もって定義しておきます。例えば\def\stepA{10}のようにしておきます。あとから簡単に編集できるようになります。

力・加速度関数のモデル

加速度を与える関数のモデルとして，次のようにしました。

\def\funcAccelX#1#2#3#4{
2*\freq * (#4) + 0*\freq * \freq * (#1) 
- \freqP * \freqP * (#1) + \PForce * (#1 - \variXCdMonkey)/sqrt((\variXCdMonkey -#1)^2 + (\variYCdMonkey -#2) ^2)^1  - \vFrac * (#3)
}
\def\funcAccelY#1#2#3#4{
-2*\freq * (#3) + 0*\freq * \freq * (#2) 
- \freqP * \freqP * (#2) + \PForce * (#2 - \variYCdMonkey)/sqrt((\variXCdMonkey -#1)^2 + (\variYCdMonkey -#2) ^2)^1 - \vFrac * (#4)}

式で書くと次のものです。

$$
\bm f = \ff(f(\bm r- \bm r_{\rm s})/r - r_{\rm s}) -\beta \bm v
$$

$\bm r$はテスト粒子の位置，$\bm r_{\rm s}$は低気圧の位置\variXCdMonkeyと\variYCdMonkey，定数$f$は低気圧が吸い込む力\PForce，$\beta$は空気抵抗の大きさ\vFracです。

このモデルでは，低気圧が吸い込む力は距離に依存しない形になっています。遠心力をキャンセルしてあります。地球上の空気は地球と一緒に自転していると遠心力が発生します。ただし，空気自体にも重力がかかり地球に貼りつくように力を受けているでしょう。この力によって遠心力が釣り合っていると仮定しました。と言うより，この仮定だとうまく再現できたというのが本音です。

他に，低気圧の座標\variXCdMonkeyと\variYCdMonkeyを運動させるために，円運動を起こす加速度関数を定義します。低気圧は偏西風に流されて西から東へ移動するからです。

0
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
0