追記
モンテカルロ法を実装してみた記事です。すっかり忘れてしまっておりました。
1. はじめに
子供向けの統計の本[1]を読んでいたところ、米粒を撒いて円周率を計算しようという記事が目に入りました。面白そうだったので、ランダムに発生させたx,yの座標のデータを使って円周率を計算してみました。
[手順]
だいたいこんな感じ
- 正方形とその正方形に内接する円を準備する。
- そこにデタラメに(ランダム)にプロットする。この デタラメに というのがポイント!
- 円の内側に入った座標と外側の座標の数から円周率を求める。
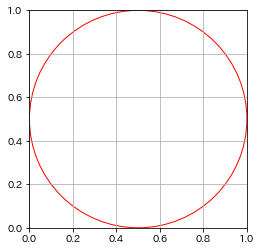
[目的]
どのくらいの座標(サンプル、つまり米粒)があれば、本当の円周率に近い値を算出できるようになるか、円周率に近い値が算出できるかを確かめてみます。
2. 実装する
実際に米粒をまいて実験するのは、難しかったのでコンピューター上で試してみました。
2-1. モジュール類をインポートする。
import numpy as np
import random
import matplotlib.pyplot as plt
import matplotlib.patches as patches
次に、いくつかのリストや定数を定義する。
今回使用するのは、辺が1の正方形と、半径が0.5の円とする。
今回の目的として、どのくらいの米粒があれば、本当の円周率に近い値が算出されるのかを調べるので、サンプル数の例を仮でn_listに定義した。
# 発生する座標の数
n_list = [10, 20, 50, 70, 100, 500, 1000, 5000, 10000, 100000,1000000]
# 円の半径
radius = 0.5
# 円周率 のリストの初期化
pi_list = []
2-2. ランダムな座標を生成する
ランダムな座標データ(デタラメに巻いた米粒に当たる)を生成する関数を定義します。
def gen_random_coordinate(n):
# 生成する座標リストの初期化
x=[]
y=[]
# 乱数によって座標を生成
x = np.random.rand(n)
y = np.random.rand(n)
return x,y
2-3. 視覚化する
実際にランダムな座標をプロットした様子を視覚化します。
# グラフの描画関数
def make_graph(x,y):
# Figureオブジェクトとそれに属する一つのAxesオブジェクトを同時に作成
fig, ax = plt.subplots()
# 円の作成
circle = patches.Circle(xy=(0.5,0.5), radius=0.5, ec='r', fill=False)
# 正しい縦横比に調整
ax.set_aspect('equal')
ax.add_patch(circle)
ax.scatter(x,y)
plt.axis('scaled')
plt.grid()
plt.xlim(0, 1.0)
plt.ylim(0, 1.0)
plt.show()
2-4. 座標データから円周率を計算する
円の内側の点の数と外側の点の数を使って円周率を計算します。
def calc_circular_constant(x,y):
# 円の内側の点の数の初期化
inner=0
# 円の外側の点の数の初期化
outer=0
# それぞれの点が円の内側か外側か点の数を数える
for xx , yy in zip(x,y):
# 円の中心からの距離を計算
dist=np.sqrt(np.square(xx-radius)+np.square(yy-radius))
if dist > radius:
outer +=1
else:
inner +=1
print('inner:outer = ', str(inner), ':', str(outer))
# 円周率を計算
pi = inner /(outer+inner) *4
pi_list.append(pi)
return pi
2-5. 実行する
上記で定義した関数をそれぞれ実行します。
どのくらいのサンプル数があれば本当の円周率に近づいていくのかを確認するのでしたね。
そこでサンプル数n_listのリストを使って順番に試してみます。
for n in n_list:
x,y = gen_random_coordinate(n)
make_graph(x,y)
print(calc_circular_constant(x,y))
3. 実験結果
以下が出力された結果です。サンプル数は10個から始まって、下に行くほど点の数が増えていきます。
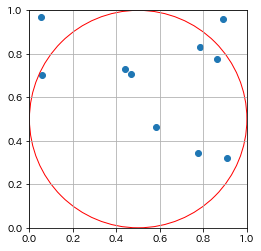
円の内側の点 : 円の外側の点 = 8 : 2
算出した円周率: 3.2
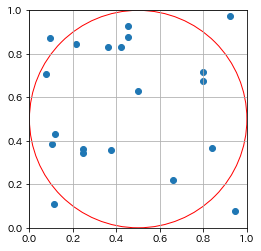
円の内側の点 : 円の外側の点 = 16 : 4
算出した円周率: 3.2
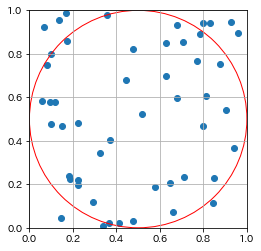
円の内側の点 : 円の外側の点 = 39 : 11
算出した円周率: 3.12
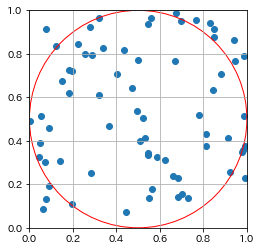
円の内側の点 : 円の外側の点 = 53 : 17
算出した円周率: 3.0285714285714285
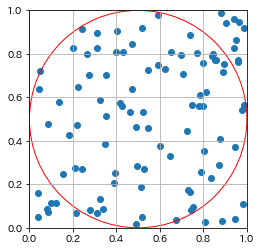
円の内側の点 : 円の外側の点 = 79 : 21
算出した円周率: 3.16
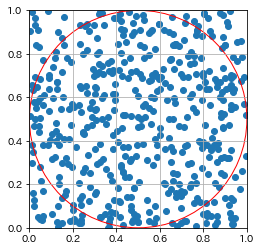
円の内側の点 : 円の外側の点 = 399 : 101
算出した円周率: 3.192

円の内側の点 : 円の外側の点 = 793 : 207
算出した円周率: 3.172
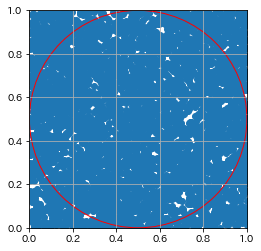
円の内側の点 : 円の外側の点 = 3894 : 1106
算出した円周率: 3.1152
円の内側の点 : 円の外側の点 = 7818 : 2182
算出した円周率: 3.1272
円の内側の点 : 円の外側の点 = 78611 : 21389
算出した円周率: 3.14444
円の内側の点 : 円の外側の点 = 785814 : 214186
算出した円周率: 3.143256
4. まとめ
今回の実験では、サンプル数が増えていくにしたがって、本当の円周率に近づいていく様子が確認されました。データ数が5000を越したあたりから、グラフが真っ青になってしまいましたね。
最終的に3.143256と、本当の円周率(3.141592653589..)と近い値になりました。
データ数が100程度であれば3.16とまだまだ程遠い。(それはそうなんですが、その理由を5に書きました。)
生成するデータにおいても一様にランダムなデータである必要があります。
上記の方法では、正規分布に従うデータを生成にしたら、まともな円周率の計算ができないでしょう。(円の内側のデータの数を使って、外側を補正すればいけるかな、また別の機会に試してみます。)
5. 最後に
今更ながら書いても100だとどんなにうまく行っても、0.04ステップで計算されるので、3.12の次は3.16になります。(上記の実験をしたかったので、この点はあまり触れませんでした。)
小学校で習う円周率のような結果を、目指すならデータ数が400必要です。(算出する円周率のステップが0.01になるため)。何度も何度もやっていれば3.14という数字が出てきそうです。
円の外側だけの米粒を数えるにしても、400粒の米粒を撒いて、何度も試行するのはなかなかタフな実験になりそうです。米粒自体の大きさもあるので、適切な大きさの紙を準備しないといけなそうです。
お子さんがいらっしゃる皆様、突然長くなった"春休み"の自由研究にいかがでしょうか。
参考文献
[1]統計ってなんの役に立つの? (著) 涌井良幸 (編)子供の科学編集部/誠文堂新光社
https://www.seibundo-shinkosha.net/book/kids/20689/