はじめに
本記事ではサポートベクターマシンについて説明します。非線形の識別関数を構成するサポートベクターマシンは、現在知られている最も認識性能の優れた学習モデルの1つと考えられています。サポートベクターマシンは未学習データに対して高い識別性能を得るための工夫があるためです。サポートベクターマシンは、基本的に二種類のクラスを識別する手法であり、文字認識などの多クラスの識別機を構成するには、サポートベクターマシンを複数組み合わせなけらばなリません。
パターン認識における学習とは
パターン認識には、まず入力から何らかの特徴量を抽出しなければなりません。そのような特徴量は通常特徴ベクトル$\mathbf x^T = [x_1,x_2,...,x_n]$と表されます。nは特徴量の個数であリます。認識対象のクラス数をKとし、クラスは$C_1,..,C_K$と表します。パターン認識における最も基本的な課題は、未知の認識対象から得られた特徴ベクトルからその対象がどのクラスに属するかを判定する識別子を開発することです。そのために、訓練データから、特徴ベクトルとクラスとの確率的な対応関係を学習することが必要である。
SVM(サポートベクターマシン)
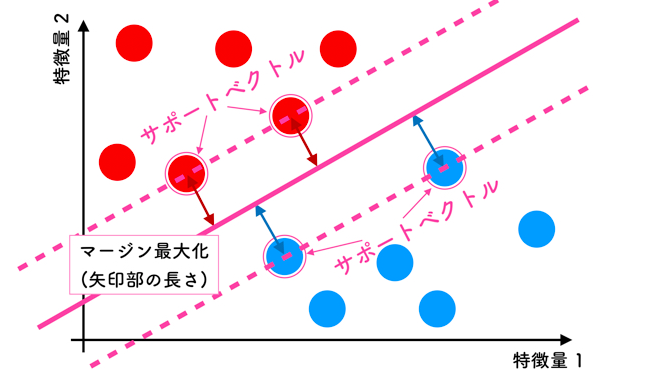
サポートベクターマシンは、ニューロンのモデルとして最も単純な線形しきい素子を用いて、2クラスのパターン識別器を構成する手法です。訓練サンプル集合から、「マージン最大化」という基準で線形しきい素子のパラメータを学習します。
ここで,上の特徴量としては2つ(2次元)なので「線」を引きますが,3次元になると「面」を引きます.
数学的に線形の場合,「直線」や「平面」の一般化として超平面という概念があるために,n次元(任意の次元)に対して求まる境界を超平面と言います。
ベクトル空間上の超平面
一般的に、ベクトル空間$\mathbf{x}$上での超空間は、以下のような式で表されます。
{\displaystyle
\mathbf{x}\mathbf{w}+w_0=0 \tag{1}
}
$\mathbf{w}$は法線ベクトルを表し、$w_0$は任意の実数を表します。
この時、ベクトル空間上の任意の$\mathbf{x_0}$とこの超平面の距離は以下のように表されます。
{\displaystyle
\frac{|\mathbf{x}_0\mathbf{w}+w_0|}{||\mathbf{w}||} \tag{2}
}
*重要
上記の式から、損失関数の最小値を与える重み$\mathbf{w}$と特徴量ベクトル$\mathbf{x_0}$との内積は、決定境界を表していたんですね。
サポートベクトルと決定境界の距離
クラスラベルを1と-1としたときに、決定境界からクラスラベルが1(+側)にあるサポートベクトルを$\mathbf{x_p}$と書いてあげます。
この時、決定境界$\mathbf{x}\mathbf{w}+w_0=0$とサポートベクトルとの距離は以下のようになります。
{\displaystyle
\frac{|\mathbf{x}_p\mathbf{w}+w_0|}{||\mathbf{w}||} \tag{3}
}
また決定境界からクラスラベルが-1(-側)にあるサポートベクトルを$\mathbf{x_m}$と書いてあげます。同様に決定境界とサポートベクトルの距離は以下になります。
{\displaystyle
\frac{|\mathbf{x}_m\mathbf{w}+w_0|}{||\mathbf{w}||} \tag{4}
}
ここがポイントです。決定境界は以下の式を満たすように重み$\mathbf{w}$を調整して無理やり決定してやります。
{\displaystyle
\mathbf{x}_p\mathbf{w}+w_0=1 \tag{5}
}
{\displaystyle
\mathbf{x}_m\mathbf{w}+w_0=-1 \tag{6}
}
重みを定数倍しても点と平面の距離は変化しないので、適当に定数倍してやることで、(5)、(6)式を満たすwを見つけることができるわけです。
{\displaystyle
\frac{|\mathbf{x}_p\mathbf{w}+w_0|}{||\mathbf{w}||} = \frac{|\mathbf{x}_m\mathbf{w}+w_0|}{||\mathbf{w}||} = \frac{1}{||\mathbf{w}||} \tag{7}
}
(7)式はサポートベクトルと決定境界との距離を表しており、これが最大化すべきマージンになります。
{\displaystyle
\frac{1}{||\mathbf{w}||} \tag{8}
}
実際は(8)式の逆数をとって2乗し、$\frac{1}{2}$をかけた値を最小化してやります。計算しやすいようにしているだけです。
{\displaystyle
\frac{1}{2}||\mathbf{w}||^2 \tag{9}
}
これを最小化するだけではなく、制約条件も考えなくてはなりません。
KKT条件
カルーシュ・クーン・タッカー条件(KKT条件)とは、非線形計画において一階導関数が満たすべき最適条件を指します。ラグランジュの未定乗数法が等式制約のみを扱うことに対し、KKT条件は、不等式制約を扱うことができる。
{\left\{
\begin{array}{ll}
最小化 & f(x) \\
制約条件 & g_i(x) \leq 0 (i=1,...,m)
\end{array}
\right.
}
この時、$f$が目的関数、$g$は不等式制約を表す関数です。KKT条件は、
{\left\{
\begin{array}{l}
\nabla f(\hat{x})+\sum_{i=1}^m \hat{\lambda_i} \nabla g_i(\hat{x})=0 \\
\hat{\lambda_i} \geq 0,g_i(\hat{x})\leq 0,\hat{\lambda_i} g_i(\hat{x}) = 0 (i=1,...,m)
\end{array}
\right.
}
マージン最大化における制約条件
(5)式で表される超平面よりクラスラベルが1側にある、トレーニングサンプル$\mathbf{x_i}$は、以下の式を満たす必要があります。
{\displaystyle
\mathbf{x}_i\mathbf{w}+w_0 \geqq 1 ~~~~~(y_i=1) \tag{10}
}
また、同様に(6)式で表される超平面よりクラスラベルが-1側にある、トレーニングサンプル$\mathbf{x_i}$は、以下の式を満たす必要があります。
{\displaystyle
\mathbf{x}_i\mathbf{w}+w_0 \leqq -1 ~~~~~(y_i=-1) \tag{11}
}
(10)、(11)式をまとめて以下のように書けます。
{\displaystyle
y_i(\mathbf{x}_i\mathbf{w}+w_0) \geqq 1 \tag{13}
}
これがマージン最大化における制約条件となります。
KKT条件を利用する
{\left\{
\begin{array}{l}
最小化 : \frac{1}{2}||w||^2 \\
制約条件 :t_i(w^Tx_i+\theta)\geq 1,(i=1,2,...,n)
\end{array}
\right.
}
ここでは、双対問題に帰着して解く方法を紹介する。まず、Lagrange乗数$\lambda_i(\geq0), i=1,..,N$を導入し、目的関数を、
L(w,\theta,\lambda)=\frac{1}{2}||w||^2-\sum_{i=1}^{N}\lambda_i\{t_i(w^Tx_i+\theta)-1\}
ここで、パラメータ$\mathbf{w}$および$\theta$に関する偏微分より、
\frac{\partial L}{\partial \theta}=\sum_{i=1}^{N}\lambda_it_i=0 \\
\frac{\partial L}{\partial w}=w-\sum_{i=1}^{N}\lambda_i t_i x_i=0 \\
$\frac{\partial L}{\partial w}$の右辺を変形すると、下記のようになる。
w=\sum_{i=1}^{N}\lambda_i t_i x_i \\
\sum_{i=1}^{N}\lambda_it_i=0
という関係が成り立つ。これらを上の目的関数の式に代入するので、$L(w,\theta,\lambda)$を計算しやすいように展開する。
L(w,\theta,\lambda)=\frac{1}{2}||w||^2-\sum_{i=1}^{N}\lambda_it_iw^Tx_i-\theta\sum_{i=1}^{N}\lambda_it_i+\sum_{i=1}^{N}\lambda_i
$L(w,\theta,\lambda)$に$\sum_{i=1}^{N}\lambda_it_i=0$,$w=\sum_{i=1}^{N}\lambda_i t_i x_i$を代入すると、
L(w,\theta,\lambda)=\frac{1}{2}||w||^2-\sum_{i=1}^{N}\lambda_it_ix_i\sum_{j=1}^{N}\lambda_j t_j x_j-\theta×0+\sum_{i=1}^{N}\lambda_i \\
L(w,\theta,\lambda)=\frac{1}{2}w\cdot w-\sum_{i=1}^{N}\sum_{j=1}^{N}\lambda_i\lambda_j t_it_j x_ix_j+\sum_{i=1}^{N}\lambda_i \\
L(w,\theta,\lambda)=\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\lambda_i\lambda_j t_it_j x_ix_j-\sum_{i=1}^{N}\sum_{j=1}^{N}\lambda_i\lambda_j t_it_j x_ix_j+\sum_{i=1}^{N}\lambda_i \\
L(w,\theta,\lambda)=-\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\lambda_i\lambda_j t_it_j x_ix_j+\sum_{i=1}^{N}\lambda_i
これを双対問題として、下記のように整理できる。
\left\{
\begin{array}{l}
最大化 : -\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\lambda_i\lambda_j t_it_j x_ix_j+\sum_{i=1}^{N}\lambda_i \\
制約条件 :\sum_{i=1}^{N}\lambda_it_i=0,\lambda_i\geq 0
\end{array}
\right. \\
これは、Lagrange乗数$\lambda_i(\geq0), i=1,..,N$に関する最適化問題となる。その解で$\lambda_i$が0でない、すなわち、$\lambda_i\geq0$となる訓練サンプル$\mathbf{x}_i$はまず2つの超平面
{\displaystyle
\mathbf{x}\mathbf{w}+w_0=1
}
{\displaystyle
\mathbf{x}\mathbf{w}+w_0=-1
}
のどちらかにのっています。このことから、$\lambda_i$が0でない訓練サンプル$\mathbf{x}_i$のことを「サポートベクター」と呼んでいます。これが、サポートベクターマシンの名前の由来です。直感的に理解できるように、一般には、サポートベクターは、もとの訓練サンプル数に比べてかなり少ないです。つまり、沢山の訓練サンプルの中から小数のサポートベクターを選び出し、それらのみを用いて線形しきい素子のパラメータが決定されることになります。
この式の$\lambda_i$が定まると、$w=\sum_{i=1}^{N}\lambda_i t_i x_i$から$\hat{w}$が定まります。
最適解$\hat{w},\hat{\theta},\hat{\lambda}$は相補性条件$\hat{\lambda_i}t_i(w^Tx_i+\theta)-1=0$を満たさなければなりません。
$t_i(w^Tx_i+\theta)-1>0$ならば、相補性条件より$\lambda_i=0$
$\lambda_i>0$を満たさないので、これは考えません。
$t_i(w^Tx_i+\theta)-1>0$の時を考えます。
目的関数は以下の手順で導出されます。
{f(x)=w^Tx+\theta,w=\sum_{i=1}^{N}\lambda_i t_i x_iより、\\
\hat{f}(x)=\sum_{i=1}^{N}\sum_{j=1}^{N}\hat{\lambda_i}t_i x_i^T x_j +\theta
}
相補性条件より、
t_i(w^Tx_i+\theta)-1=0,w=\sum_{i=1}^{N}\lambda_i t_i x_iより、\\
t_i(\sum_{i=1}^{N}\sum_{j=1}^{N}\hat{\lambda_i}t_i x_i^T x_j+\theta)-1=0
両辺を$t_i$で割ると
\sum_{i=1}^{N}\sum_{j=1}^{N}\hat{\lambda_i}t_i x_i^T x_j+\theta - \frac{1}{t_i}=0
$\theta$以外の項を移項して
\theta=\frac{1}{t_i} -\sum_{i=1}^{N}\sum_{j=1}^{N}\hat{\lambda_i}t_i x_i^T x_j
$\frac{1}{t_i}$は$t_i\in {1,-1}$であることから$t_i$と等しいので、
\theta=t_i -\sum_{i=1}^{N}\sum_{j=1}^{N}\hat{\lambda_i}t_i x_i^T x_j
したがって、
{\hat{f}(x)=\sum_{i=1}^{N}\sum_{j=1}^{N}\hat{\lambda_i}t_i x_i^T x_j + \frac{1}{N_S} \sum_{n \in S}(t_n - \sum_{m \in S}\hat{\lambda}_mt_m x_n^T x_m)
}
参考文献
http://www.msi.co.jp/nuopt/glossary/term_da98193bc878eb73f1624989004cfa809e13590a.html
https://home.hiroshima-u.ac.jp/tkurita/lecture/svm.pdf
https://kenyu-life.com/2019/02/11/support_vector_machine/