再帰関数

はじめに、 木情報源であったり、決定木アルゴリズムだったり、木構造の再帰を使う機会が多いので、再帰関数についてまとめたいと思います。
自分自身を実行する関数を再帰関数といい、再帰関数内の自分自身の実行箇所を再帰呼び出しと言います。

recursive.ipynb

def recursive_f(depth):
  print("depth: "+ str(depth))
  if depth == 10:
    return 
  recursive_f(depth + 1)

if __name__=="__main__":
  recursive_f(0)

実行結果は次のようになります。
depth: 0
depth: 1
depth: 2
depth: 3
depth: 4
depth: 5
depth: 6
depth: 7
depth: 8
depth: 9
depth: 10

自分自身を呼び出すので、どこかで条件分岐をしてあげなければ無限に実行が続きます。

決定木で実装する時は、ノードクラスを作ってやり、自分の子ノードを格納するメンバ変数を持たせ、自分を分割して子ノードを生成するメンバ関数を再帰関数化してやればいいです。自分の子ノードとなるメンバ変数が、更に孫ノードとなるメンバ変数を持ち、更に曽孫ノードとなるメンバ変数を持ち、、の様に永遠に子ノードを生成します。
簡単のため、深さが3のときの図を表すと、

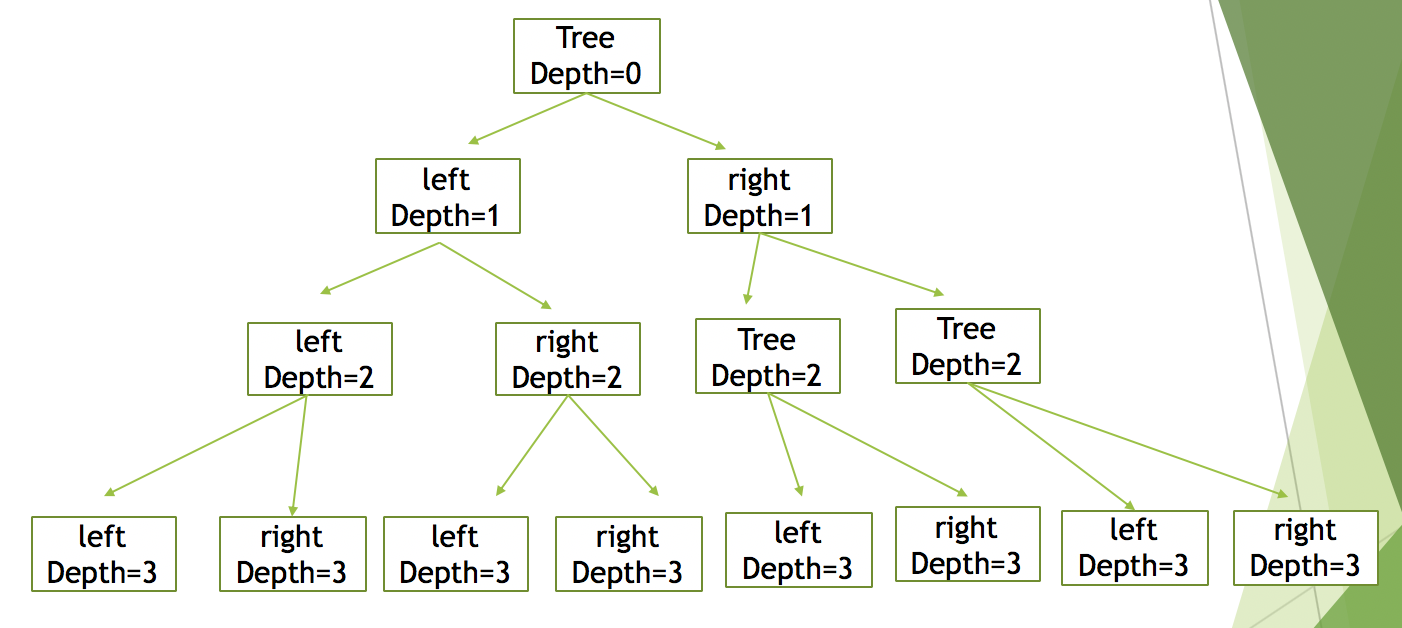
これをコード化してあげると

recursive_tree.ipynb

class Node:
  def __init__(self, max_depth):
    self.left = None
    self.right = None
    self.max_depth = max_depth
    self.depth = None

  def split_node(self, depth):
      self.depth = depth
      print("depth: " + str(self.depth))

      if self.depth == self.max_depth:
          return

      self.left  = Node(self.max_depth)
      self.right = Node(self.max_depth)

      self.left.split_node(depth + 1)   # recursive call
      self.right.split_node(depth + 1)  # recursive call

if __name__ == "__main__":
    max_depth = 3
    initial_depth = 0

    tree = Node(max_depth)
    tree.split_node(initial_depth)

実行結果
depth: 0
depth: 1
depth: 2
depth: 3
depth: 3
depth: 2
depth: 3
depth: 3
depth: 1
depth: 2
depth: 3
depth: 3
depth: 2
depth: 3
depth: 3
以上が、再帰関数の利用例です。この考え方を身につけると決定木アルゴリズムが実装しやすいのでぜひ試してみましょう。