Pythonで線形予測分析 (LPC) を学ぶ

はじめに

LPCは音声分析の基本であり、通常は自分でプログラムを書かずとも便利なパッケージが利用できる。しかし、その中身を本当に理解しようと思ったら、やはり自分でプログラムを書いてみるのが一番である。

ここでは、線形予測モデルおよび線形予測分析 (LPC) の原理を説明し、Pythonによって線形予測係数を求めてみる。

Google Colaboratory 上ですぐに試せるノートブック LPC.ipynbも用意しているので、活用願いたい。

音声の線形予測モデル

時刻 $n$ において標本化された音声信号を $s(n)$ と書く。もし、時刻 $n$ での値が過去の値から予測することができ、しかも過去の値の線形結合で表されるとすると、以下のように書くことができる。
$$s(n)+a_1s(n-1)+a_2s(n-2)+\cdots a_ps(n-p)\approx 0 \tag{1} $$
もちろん、実際の音声信号は過去の値だけから予測することはできない。予測しきれなかった成分を $e(n)$ と書くと、式(1)は次のように書き直せる。
$$s(n)=-\sum_{i=1}^p a_is(n-i)+e(n) \tag{2}$$
この式からも明らかなように、誤差 $e(n)$ は、過去何個の値を使って予測するか、また係数 $a_i$ をどのように選ぶかに依存して決まる。
音声信号から $e(n)$ の二乗平均値を最小にする $a_i$ の組を求めることを線形予測分析と呼ぶ。また、このときの $a_i$ を線形予測係数、 $e(n)$ を線形予測残差と呼ぶ。

次に、音声の分析において線形予測係数が持つ意味について述べる。ディジタル信号のような離散時間信号や離散時間システムを取り扱う際には、 $z$ 変換が用いられる。連続時間信号や連続時間システムにおけるラプラス変換が線形微分方程式の代数的解法を与えるのと同じように、 $z$ 変換は式(2)のような線形差分方程式を代数的に取り扱うことを可能にする。

ある信号を時間 $i$ だけ遅らせると、その信号の $z$ 変換には $z^{-i}$ が乗じられる。したがって、式(2)の両辺を $z$ 変換すると
$$S(z)=-\sum_{i=1}^p a_iS(z)z^{-i}+E(z) \tag{3}$$
ただし、 $S(z)$ , $E(z)$ はそれぞれ $s(n)$, $e(n)$ の $z$ 変換である。これを変形すると、以下の式を得る。
$$S(z)=\frac{1}{\displaystyle 1+\sum_{i=1}^p a_iz^{-i}}E(z) \tag{4}$$
ここで、 $A(z)=1+\sum_{i=1}^p a_iz^{-i}$ とおくと、
$$S(z)=\frac{1}{A(z)}E(z) \tag{5}$$
以下の図は、式(5)を信号システム的に解釈したブロック線図である。

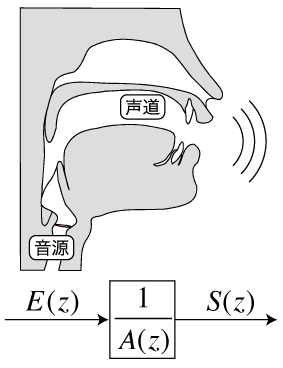
音声信号 $S(z)$ は、入力信号 $E(z)$ を伝達関数が $\frac{1}{A(z)}$ で与えられるシステムに通した出力であると考えることができる。人間の音声は、喉頭で発生した音源波(有声音なら声帯振動、無声音なら乱流が音源となる)が、声道というシステムを通って生成されるので、音声の生成過程を線形予測分析と対照させて考えると、 $\frac{1}{A(z)}$ は声道の伝達関数に、 $E(z)$ は音源に対応することがわかる。実際、このモデルは人間の音声生成過程をそれなりによく表現している。というのは、式の形からわかるように、システムの伝達関数 $\frac{1}{A(z)}$ は $p$ 個の極を持ち、零点を持たない。一方、声道を長さが等しく断面積が異なる $p$ 個の一様音響管を1本につないだものと近似した場合、伝達関数がこの形になることが証明できる。/m/ /n/のような鼻音などではこの近似は必ずしも妥当ではないが、総合的には、極しか持たないシステムによる音声のモデル化はたいへん有用であると考えられている。

声道フィルタの推定

音声の分析とは、狭い意味では、音声信号から声道フィルタを推定し、音声信号を音源と声道フィルタとに分離することを意味する。音声の分析手法には、線形予測分析のほかにも、メルケプストラム法やSTRAIGHTなどがある。ここでは、音声の線形予測モデルにおける線形予測係数 $a_1, a_2, \cdots a_p$ を推定する方法の概略を説明する。線形予測係数が決まれば、声道フィルタは
$$H(z)=\frac{1}{A(z)}=\frac{1}{1+\displaystyle\sum_{i=1}^p a_iz^{-i}}$$により決まる。

ここでは、式(1)のような、過去 $p$ 個の値から現在の値を予測したもの(前向き予測)のほかに、未来の $p$ 個の値から現在の値を予測したもの(後向き予測)を用いる。 $N$ 点の音声信号 $s(0),s(1),\cdots s(N-1)$ に対し、前向き予測 $\hat s_f(n)$ および後向き予測 $\hat s_b(n)$ は以下で定義される。
$$\begin{align}
\hat s_f(n)&=-\sum_{i=1}^p a_is(n-i) \tag{6} \\
\hat s_b(n)&=-\sum_{i=1}^p a_is(n+i) \tag{7}
\end{align}$$
ただし、 $s(n)$ は窓かけされて切り出された音声信号で、時刻 $n=p$ よりも前および$ n=N-p-1$ よりも後で値を持たないと仮定している。

ここで、 $p$ 個の線形予測係数から予測したときの前向き誤差 $f_p(n)$ および後向き誤差 $b_p(n)$ を定義する。

$$\begin{align}
f_p(n)&=s(n)-\hat s_f(n)=s(n)+\sum_{i=1}^p a_is(n-i)=\sum_{i=0}^p a_is(n-i) \tag{8} \\
b_p(n)&=s(n)-\hat s_b(n)=s(n)+\sum_{i=1}^p a_is(n+i)=\sum_{i=0}^p a_is(n+i) \tag{9}
\end{align}$$

ただし、 $a_0=1$ とおいた。

これらから、前向き誤差二乗和 $F_p$ および後向き誤差二乗和 $B_p$ は
$$\begin{align}
F_p&=\sum_{n=0}^{N-1}f_p(n)^2=\sum_{n=p}^{N-1}f_p(n)^2 \tag{10} \\
B_p&=\sum_{n=0}^{N-1}b_p(n)^2=\sum_{n=0}^{N-p-1}b_p(n)^2 \tag{11}
\end{align}$$
と定義される。

正規方程式

誤差二乗和を最小にする $a_1, a_2, \cdots a_p$ を求めたいので、 $F_p$ をそれぞれで偏微分してゼロとおくと以下が得られる。
$$\sum_{n=0}^{N-1} s(n-i)s(n)=-\sum_{k=1}^p
a_k\sum_{n=0}^{N-1}s(n-i)s(n-k) \tag{12}
$$

ここで式(12)を自己相関関数
$$
r(i-k)=\sum_{n=-\infty}^\infty s(n)s(n-i+k)
=\sum_{n=0}^{N-1} s(n-i)s(n-k) \tag{13}
$$
によって表すと
$$
r(i)=-\sum_{k=1}^p a_kr(|i-k|) \tag{14}
$$
となる。この式が $i=1,2,\cdots p$ について成り立つ。これらの連立方程式
を行列形式で書くと
$$
\begin{bmatrix} r(0) & r(1) & r(2) & \cdots & r(p-1) \\ r(1) & r(0) & r(1) & \cdots & r(p-2) \\ r(2) & r(1) & r(0) & \cdots & r(p-3) \\ \vdots & \vdots & \vdots & & \vdots \\ r(p-1) & r(p-2) & r(p-3) & \cdots & r(0) \end{bmatrix} \begin{bmatrix} -a_1 \\ -a_2 \\ -a_3 \\ \vdots \\ -a_p \end{bmatrix} = \begin{bmatrix} r(1) \\ r(2) \\ r(3) \\ \vdots \\ r(p) \end{bmatrix} \tag{15}
$$

正規方程式を直接解く

線形予測係数 $a_1, a_2, \cdots a_p$ は、正規方程式(15)を解けば求まる。簡単のため、以下式(15)を $\mathbf{R}\mathbf{a}=\mathbf{r}$ と書く。

まず、練習のため小さいデータでテストしてみる。

import numpy as np
x7=np.array([2,3,-1,-2,1,4,1],dtype='float64')

自己相関関数の定義式(13)通りに計算すると

N=len(x7)
xpad=np.pad(x7,[0,N-1],'constant')
r=[np.sum(xpad[0:N] * xpad[lag:lag+N]) for lag in range(N)]

>>> r

[36.0, 11.0, -16.0, -7.0, 13.0, 11.0, 2.0]

自己相関関数は、numpy.correlateを使うともっと簡単に計算できる。

autocorr = np.correlate(x7,x7,mode='full')

>>> autocorr

array([  2.,  11.,  13.,  -7., -16.,  11.,  36.,  11., -16.,  -7.,  13.,
        11.,   2.])

↑真ん中の値が $r(0)=36$, 次の値が $r(1)=11$ ... と、正しく計算できている。

ここでは $p=3$ として線形予測係数を求めてみる。まず式(15)左辺の $\mathbf{R}$ は

p = 3
R = np.zeros((p,p));
for lag in range(p):
    ci = len(x7)-1-lag;
    R[lag,] = autocorr[ci:ci+p]

>>> R

array([[ 36.,  11., -16.],
       [ 11.,  36.,  11.],
       [-16.,  11.,  36.]])

次に式(15)右辺の $\mathbf{r}$ は

r = autocorr[len(x7):len(x7)+p]

>>> r

array([ 11., -16.,  -7.])

では $\mathbf{a}$ を求めてみよう。

>>> -np.linalg.solve(R,r)

array([-0.69190537,  0.76150628, -0.34575153])

1行で書けてしまうが、 $p$ が大きいと計算コストが大きそうだ。

Levinson-Durbin法

正規方程式(15)を少し変形して
$$
\begin{bmatrix} r(1) & r(0) & r(1) & r(2) & \cdots & r(p-1) \\ r(2) & r(1) & r(0) & r(1) & \cdots & r(p-2) \\ r(3) & r(2) & r(1) & r(0) & \cdots & r(p-3) \\ \vdots & \vdots & \vdots & \vdots & & \vdots \\ r(p) & r(p-1) & r(p-2) & r(p-3) & \cdots & r(0) \end{bmatrix} \begin{bmatrix} 1 \\ a_1 \\ a_2 \\ a_3 \\ \vdots \\ a_p \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ \vdots \\ 0 \end{bmatrix} \tag{16}
$$

ここで、
$$
E_p=\sum_{k=0}^p a_k r(k) \tag{17}
$$
とおくと、式(16)は
$$
\begin{bmatrix} r(0) & r(1) & r(2) & r(3) & \cdots & r(p) \\ r(1) & r(0) & r(1) & r(2) & \cdots & r(p-1) \\ r(2) & r(1) & r(0) & r(1) & \cdots & r(p-2) \\ r(3) & r(2) & r(1) & r(0) & \cdots & r(p-3) \\ \vdots & \vdots & \vdots & \vdots & & \vdots \\ r(p) & r(p-1) & r(p-2) & r(p-3) & \cdots & r(0) \end{bmatrix} \begin{bmatrix} 1 \\ a_1 \\ a_2 \\ a_3 \\ \vdots \\ a_p \end{bmatrix} = \begin{bmatrix} E_p \\ 0 \\ 0 \\ 0 \\ \vdots \\ 0 \end{bmatrix} \tag{18}
$$
となる。このときの係数行列を $N_p$, 線形予測係数ベクトルを $A_p$ と書くと、
$$
N_pA_p=\begin{bmatrix} E_p \\ 0 \\ 0 \\ 0 \\ \vdots \\ 0 \end{bmatrix} \tag{19}
$$
となる。

この方程式を高速に解く方法はLevinson-Durbin法として知られている。Levinson-Durbin法は、サイズ $p$ における解を基にサイズ $p+1$ における解を求める再帰的アルゴリズムである。今、 $A_p$, $N_p$, $E_p$ が既に求まっているとする。ここで、 $A_p$ の一番下にゼロを追加したベクトルを $U_{p+1}$ とする。式(18)より
$$
\begin{bmatrix} r(0) & r(1) & r(2) & \cdots & r(p+1) \\ r(1) & r(0) & r(1) & \cdots & r(p) \\ r(2) & r(1) & r(0) & \cdots & r(p-1) \\ \vdots & \vdots & \vdots & & \vdots \\ r(p) & r(p-1) & r(p-2) & \cdots & r(1) \\ r(p+1) & r(p) & r(p-1) & \cdots & r(0) \end{bmatrix} \begin{bmatrix} 1 \\ a_1 \\ a_2 \\ \vdots \\ a_p \\ 0 \end{bmatrix} = \begin{bmatrix} E_p \\ 0 \\ 0 \\ \vdots \\ 0 \\ \displaystyle\sum_{j=0}^p a_jr(p+1-j) \end{bmatrix} \tag{20}
$$
すなわち
$$
N_{p+1}U_{p+1}=\begin{bmatrix} E_p \\ 0 \\ 0 \\ \vdots \\ 0 \\ \displaystyle\sum_{j=0}^p a_jr(p+1-j) \end{bmatrix}\tag{21}
$$
となる。

$U_{p+1}$ の上下を逆にしても等式が成り立つようにするためには、係数行列の列の左右を逆にすればよい。
$$
\begin{bmatrix} r(p+1) & r(p) & r(p-1) & \cdots & r(0) \\ r(p) & r(p-1) & r(p-2) & \cdots & r(1) \\ r(p-1) & r(p-2) & r(p-3) & \cdots & r(2) \\ \vdots & \vdots & \vdots & & \vdots \\ r(1) & r(2) & r(3) & \cdots & r(p) \\ r(0) & r(1) & r(2) & \cdots & r(p+1) \end{bmatrix} \begin{bmatrix} 0 \\ a_p \\ a_{p-1} \\ \vdots \\ a_1 \\ 1 \end{bmatrix} = \begin{bmatrix} E_p \\ 0 \\ 0 \\ \vdots \\ 0 \\ \displaystyle\sum_{j=0}^p a_jr(p+1-j) \end{bmatrix} \tag{22}
$$
さらに、右辺の上下を逆にしても等式が成り立つようにするためには、係数行列の行の上下を逆にすればよい。
$$
\begin{bmatrix} r(0) & r(1) & r(2) & \cdots & r(p+1) \\ r(1) & r(0) & r(1) & \cdots & r(p) \\ r(2) & r(1) & r(0) & \cdots & r(p-1) \\ \vdots & \vdots & \vdots & & \vdots \\ r(p) & r(p-1) & r(p-2) & \cdots & r(1) \\ r(p+1) & r(p) & r(p-1) & \cdots & r(0) \end{bmatrix} \begin{bmatrix} 0 \\ a_p \\ a_{p-1} \\ \vdots \\ a_1 \\ 1 \end{bmatrix} = \begin{bmatrix} \displaystyle\sum_{j=0}^p a_jr(p+1-j) \\ 0 \\ 0 \\ \vdots \\ 0 \\ E_p \end{bmatrix} \tag{23}
$$
よって、 $U_{p+1}$ の上下を逆にしたベクトルを $V_{p+1}$ と書くと、
$$
N_{p+1}V_{p+1}=\begin{bmatrix} \displaystyle\sum_{j=0}^p a_jr(p+1-j) \\ 0 \\ 0 \\ \vdots \\ 0 \\ E_p \end{bmatrix} \tag{24}
$$
となる。

ここで、求めたい $A_{p+1}$ が、$U_{p+1}$ と $V_{p+1}$ により以下のように表せると仮定する。
$$
A_{p+1}=U_{p+1}+k_pV_{p+1}
\tag{25}
$$

$k_p$ は反射係数またはPARCOR係数と呼ばれる。式(21)および式(24)より、
$$
N_{p+1}A_{p+1}=N_{p+1}(U_{p+1}+k_pV_{p+1})=\begin{bmatrix} \displaystyle E_p+k_p\sum_{j=0}^p a_jr(p+1-j) \\ 0 \\ 0 \\ \vdots \\ 0 \\ \displaystyle\sum_{j=0}^p a_jr(p+1-j)+k_pE_p \end{bmatrix} \tag{26}
$$
となる。サイズ $p$ において解くべき式は式(19)であり、サイズを $p+1$ にしてもこの式が成り立つようにするためには、式(26)右辺の一番下の要素がゼロになるように $k_p$ を決めればよいことがわかる。したがって
$$
k_p=-\frac{\displaystyle\sum_{j=0}^p a_jr(p+1-j)}{E_p}
\tag{27}
$$
とし、それから式(26)右辺の一番上の要素が $E_{p+1}$ になるようにする。
$$
E_{p+1}=E_p+k_p\sum_{j=0}^p a_jr(p+1-j)=E_p+k_p(-E_pk_p)=E_p(1-k_p^2) \tag{28}
$$

Levinson-Durbin法で解く

Levinson-Durbin法は再帰アルゴリズムなので、初期条件が必要となる。$p=1$ のとき $\begin{bmatrix}r(0) & r(1) \\ r(1) & r(0)\end{bmatrix}\begin{bmatrix}1\\a_1\end{bmatrix}=\begin{bmatrix}E_1\\0\end{bmatrix}$ より
$$\begin{align}
a_1&=-r(1)/r(0) \\
E_1&=r(0)+r(1)a_1
\end{align}$$
となるので、これらを初期条件とする。

Python のコードは以下の通り。

import numpy as np

def levinson(signal, order, r=None):
    p = order

    if r is None:
        x = signal
        autocorr = np.correlate(x,x,mode='full')
        return levinson(signal, order, autocorr[len(x)-1:len(x)+p])
    
    if p == 1:
        a = np.array([1, -r[1] / r[0]])
        E = a.dot(r[:2])
    else:
        aa, EE = levinson(signal, p-1, r)
        kk = -(aa.dot(r[p:0:-1])) / EE
        U = np.append(aa, 0)
        V = U[::-1]
        a = U + kk * V
        E = EE * (1 - kk * kk)

    return a, E

では、今作った levinson 関数を使い、 $p=3$ として上で使った小さいデータで試してみる。

>>> levinson(x7,3)[0]

array([ 1.        , -0.69190537,  0.76150628, -0.34575153])

solveで解いた場合と同じ結果になった。

いよいよ、Levinson-Durbin法で音声を分析してみよう。
Praatを使って母音 /a/ の1フレーム分を切り出し、プリエンファシス、窓かけをして作ったサンプル音声が https://www.dropbox.com/s/l370mky5255w14v/a_11025_preemp_part.wav?dl=0 からダウンロードできる。

Filter (pre-emphasis): 50
Extract part: 0, 0.025, "Hamming", 1, "no"
Save as WAV file: "a_11025_preemp_part.wav"

Waveファイルは Scipy の機能を利用して読み込む。

from scipy.io.wavfile import read
fs, x = read("a_11025_preemp_part.wav")

fs を確認すればわかるように、標本化周波数は11025Hzである。周波数の上限が約5500Hzなので、男性の場合には第5フォルマントあたりまで入る。これを2倍して10次で分析すればよさそうだが、少し余裕を持たせて12次で分析してみる。

>>> a = levinson(x/32768,12)
>>> a

(array([ 1.        , -1.75325333,  1.97953403, -1.80343314,  1.20047156,
         0.00740131, -0.46918192,  0.74669944, -0.81144139,  0.5992474 ,
        -0.22257812,  0.12155728,  0.04168977]),

計算結果の確認

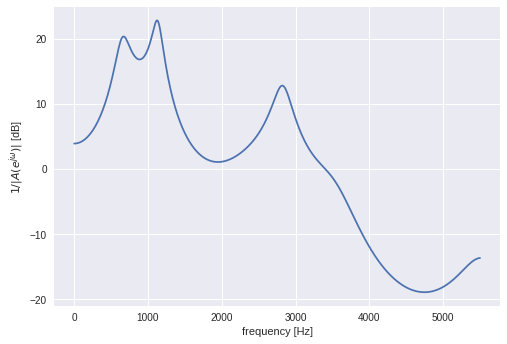
LPC係数は求まったが、これ自体はあまり有用でない。応用例として、まず推定された声道の伝達関数 $\frac{1}{A(z)}$ の周波数応答 $\frac{1}{A(e^{j\omega})}$ を描いてみる。これはLPCスペクトルと呼ばれ、声道の共鳴特性を推定したものと解釈できる。

from scipy import signal
import matplotlib.pyplot as plt

w, h = signal.freqz(1, a)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(fs * w / 2.0 / np.pi, 20 * np.log10(np.abs(h)))
ax.set_xlabel('frequency [Hz]')
ax.set_ylabel('$1 / |A(e^{j\omega})|$ [dB]')
plt.show()

次にフォルマント周波数（声道の共振点）を求める。LPCスペクトルの図からも、だいたいのフォルマント周波数は読み取れるが、もっと直接には、伝達関数の極（$A(z)=0$ の解）の偏角を求めればよい。

poles = np.roots(a)
intns = np.abs(poles)
ff = np.angle(poles) * fs / 2.0 / np.pi
formantfreq = ff[(ff > 10) & (ff < fs / 2.0 - 10) & (intns > 0.8)]

>>> formantfreq
array([ 654.25498445, 1131.49529868, 2826.79106331, 3539.34285059])

$F_1=654$ [Hz], $F_2=1131$ [Hz], $F_3=2827$ [Hz] であることがわかった。

Burg法

Levinson-Durbin法を改良したBurg法では、前向き誤差二乗和 $F_p$ のかわりに、前向き誤差二乗和と後向き誤差二乗和の和 $F_{p}+B_{p}$ を最小にする $k_p$ を求める。パラメータの更新式(25)を各要素ごとに書くと、新しいパラメータ $\hat a_n$ は
$$
\hat a_n=a_n+k_p a_{p+1-n} \tag{29}
$$
と書けるので、サイズ $p+1$ の前向き誤差 $f_{p+1}(n)$ は、既に求まっているサイズ $p$ の前向き誤差 $f_p(n)$ および後向き誤差 $b_p(n)$ を利用して以下のように求められる。
$$\begin{align}
f_{p+1}(n)&=\sum_{i=0}^{p+1}\hat a_is(n-i) \\
&=\sum_{i=0}^{p+1}a_i s(n-i)+k_p\sum_{i=0}^{p+1}a_{p+1-i}s(n-i) \\
&=\sum_{i=0}^{p+1}a_i s(n-i)+k_p\sum_{j=0}^{p+1}a_js(n-p-1+j) \\
&=f_p(n)+k_pb_p(n-p-1) \tag{33}
\end{align}$$

同様に、
$$\begin{align}
b_{p+1}(n)&=\sum_{i=0}^{p+1}\hat a_i s(n+i) \\
&=\sum_{i=0}^{p+1}a_i s(n+i)+k_p\sum_{i=0}^{p+1}a_{p+1-i}s(n+i) \\
&=\sum_{i=0}^{p+1}a_i s(n+i)+k_p\sum_{j=0}^{p+1}a_js(n+p+1-j) \\
&=b_p(n)+k_p f_p(n+p+1) \tag{37}
\end{align}$$

式(33)および式(37)を式(10)および式(11)に代入すると、
$$
F_{p+1}+B_{p+1}=\sum_{n=p+1}^{N-1}{f_p(n)+k_pb_p(n-p-1)}^2
+\sum_{n=0}^{N-p-2}{b_p(n)+k_p f_p(n+p+1)}^2
$$
これを $k_p$ で微分してゼロとおくと以下が得られる。
$$
k_p=\frac{-2\displaystyle\sum_{n=0}^{N-p-2}f_p(n+p+1)b_p(n)}{\displaystyle\sum_{n=p+1}^{N-1}f_p(n)^2
+\displaystyle\sum_{n=0}^{N-p-2}b_p(n)^2} \tag{39}
$$

Burg法によって線形予測係数 $a_1, a_2, \cdots a_P$ を求める手順を以下にまとめる。

1. $A_0=[1]$ とする。
2. $f_0(n)$ および $b_0(n)$ を求める。(式(8),(9)より、これらは $s(n)$ に一致する。)
3. 0から $P-1$ までの $p$ に対して以下を実行する。
   1. 式(39)から $k_p$ を求める。
   2. 式(29)から新しい $A_{p+1}$ を求める。
   3. 式(33)から新しい $f_{p+1}(n)$ を求める。
   4. 式(37)から新しい $b_{p+1}(n)$ を求める。

Burg法で解く

Python のコードは以下の通り。

def burg(signal, order):
    x = signal
    P = order
    a = np.zeros(P+1)
    k = np.zeros(P)
    a[0] = 1

    f = np.copy(signal)
    b = np.copy(signal)

    N = len(f)
    for p in range(P):
        kf = f[p+1:]
        kb = b[:N-p-1]
        D = np.sum(kf * kf) + np.sum(kb * kb)
        k[p] = -2 * np.sum(kf * kb) / D
        U = a[0:p+2]
        V = U[::-1]
        a[0:p+2] = U + k[p] * V
        fu = k[p] * b[:N-p-1]
        bu = k[p] * f[p+1:]
        f[p+1:] += fu
        b[:N-p-1] += bu

    return a, k

最初は、例によって小さいデータから。

>>> burg(x7,3)[0]

array([ 1.        , -1.06504044,  1.15723817, -0.57716927])

Burg法はLevinson-Durbin法と考え方が違うので、結果も少し異なる。

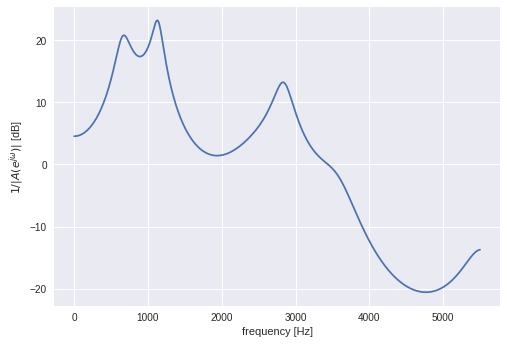
次に、母音 /a/ を分析してみる。

>>> a, k = burg(x/32768,12)
>>> a

(array([ 1.        , -1.85021097,  2.2136297 , -2.13681875,  1.54085786,
        -0.23213449, -0.44762501,  0.92234581, -1.10971129,  0.9122223 ,
        -0.47052016,  0.25859827, -0.00824584]),

w, h = signal.freqz(1, a)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(fs * w / 2.0 / np.pi, 20 * np.log10(np.abs(h)))
ax.set_xlabel('frequency [Hz]')
ax.set_ylabel('$1 / |A(e^{j\omega})|$ [dB]')
plt.show()