多重比較とは
ある変数によってデータを群1,群2,群3に分けたとき、それらの母平均が全部同じでなければ、その変数は平均値に影響すると言える。しかし、だからと言って全てのペアの母平均に差があるとは限らない。そこで、どの群とどの群に間に母平均の差があるかを調べたい。これが多重比較である。
多重比較は、分散分析の下位検定として実施されることが多い。分散分析は線形モデル(LM)の一種である。分散分析や、それとセットで使われるTukeyのHSD検定などの多重比較では、誤差が正規分布に従うことを仮定している。
誤差が正規分布に従わない一般化線形モデル(GLM)では、線形モデルを前提とした多重比較が使えない。
正規分布モデル以外の場合に $t$ 分布のような理論分布を導くことは難しい。尤度比検定は、このような場合でも使える統計的検定である。しかし、尤度比検定はネストされたモデルに対してしか使えないので、一般の多重比較に適用することはできない。
モデル選択
統計的検定以外の方法はNG、という人以外は、モデル選択による多重比較を検討すべきである。
モデル選択では、ある変数が有効であるか否かを検証するため、その変数を入れたモデルと外したモデルそれぞれの予測力を比較する。外したモデルの方が高い予測力を持つならば、その変数は有効ではない、と結論する。モデルの予測力はAICで評価する。
モデル選択に基づいて多重比較をする場合には、各群を統合した再グルーピングを行う。全てのグルーピングの可能性の中で、AICが最小となるものを探す。例えば群1と群2を統合したグルーピング (1,2)(3)が最良ならば、群1と群2の間に平均値の差はなく、群1,2と群3の間に平均値の差はある、と結論づける。
例題データ
ここでは例として経過時間の分布の比較を取り上げる。nycflights13 を元に、少し加工して例題データを作る。
ラ・ガーディア空港(LGA)発デトロイト空港(DTW)行の便の飛行時間が航空会社によって変わるかどうかを検証する。最短時間で飛んだ便に対して相対的に何分余計に飛んだかを relativetime という列に入れる。
library(tidyverse)
library(nycflights13)
flights %>%
filter(origin=="LGA",dest=="DTW",!is.na(air_time)) %>%
dplyr::select(carrier,air_time) %>%
mutate(carrier=as_factor(carrier)) %>%
mutate(relativetime=air_time-min(air_time)) %>%
filter(relativetime>0) -> data
data
carrier air_time relativetime
1 MQ 105 39
2 DL 105 39
3 DL 110 44
4 MQ 103 37
5 MQ 112 46
6 DL 104 38
7 DL 108 42
8 MQ 102 36
9 DL 94 28
10 MQ 106 40
# … with 4,897 more rows
航空会社ごとの平均時間を求める。
data %>%
group_by(carrier) %>%
summarise(meanreltime=mean(relativetime))
carrier meanreltime
1 MQ 19.0
2 DL 17.7
3 9E 24.3
4 EV 15.3
9E > MQ > DL > EV であるように見える。後ほどこれを検証する。
箱ひげ図で分布を比較する。
ggplot(data) +
geom_boxplot(aes(x=carrier,y=relativetime))
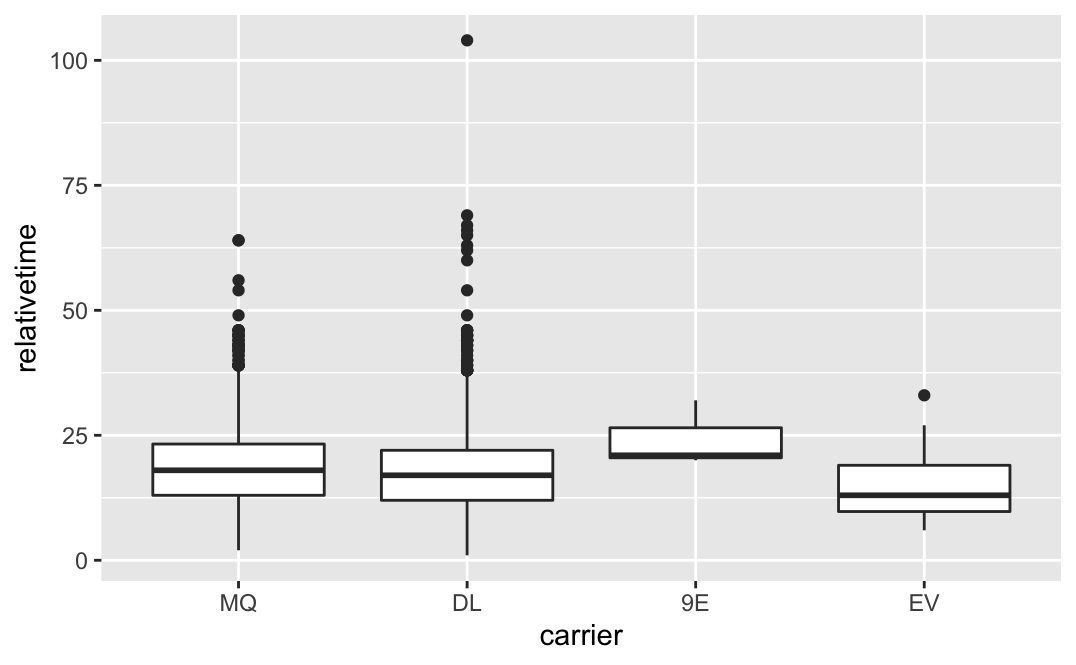
全般に、分布は対称でなく、遅れる方向にすそが長い分布に見える。デルタ航空(DL)についてヒストグラムを描いてみる。
data %>%
filter(carrier=="DL") %>%
ggplot() +
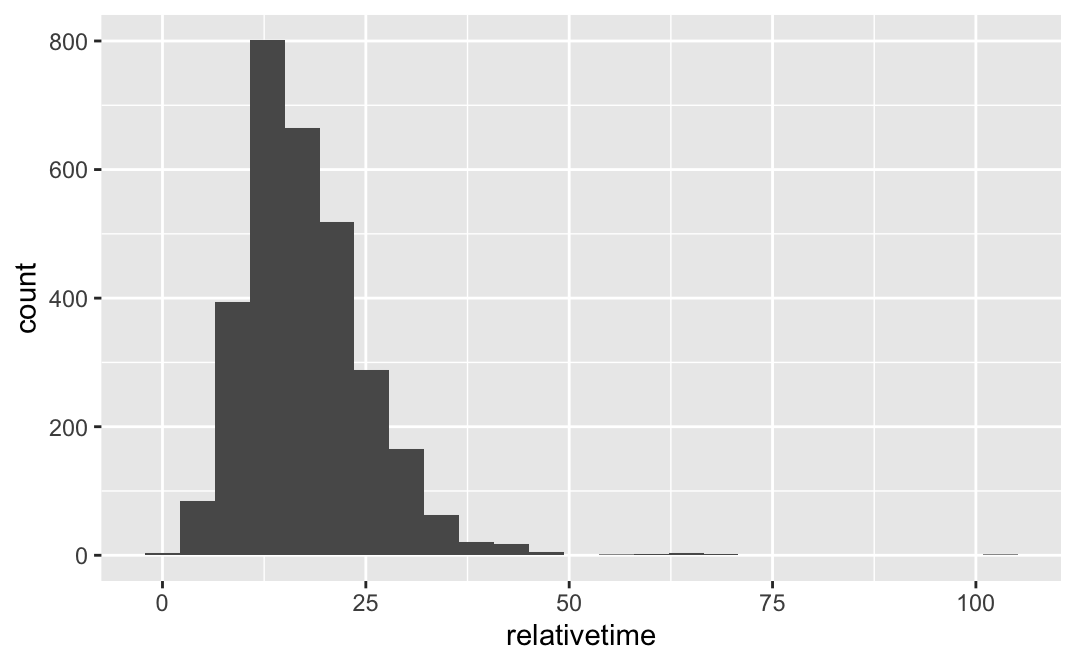
geom_histogram(aes(x=relativetime),bins=25)
時間の分布は負の値を取らず、右に歪んだ分布となることが多い。このような分布を正規分布で表すのは不適当である。
ガンマ分布
このような時間の分布を表すための理論分布としてはガンマ分布が用いられる。
確率変数 $x$ の確率密度関数がパラメータ $k$, $\theta$ をもつ次式であるとき、 $x\sim\text{Gamma}(k,\theta)$ と表記する。
$$p(x;k,\theta)=\frac{1}{\Gamma(k)\theta^k}x^{k-1}e^{-x/\theta}$$
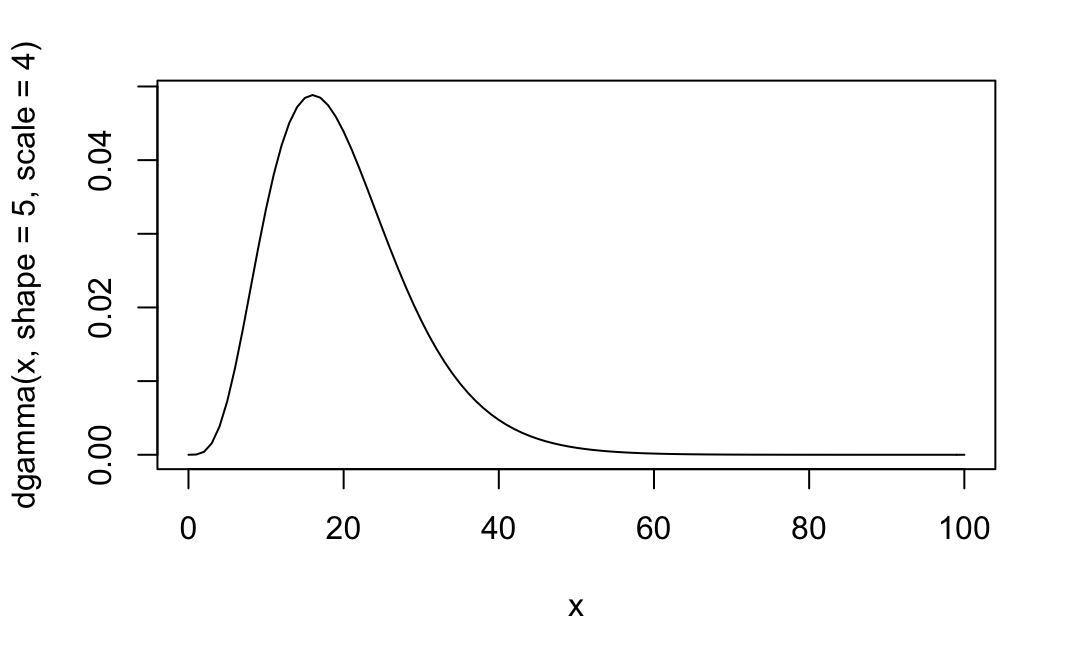
下図は、 $k$ (shapeパラメータ)が5, $\theta$ (scaleパラメータ)が4の場合のガンマ分布の確率密度関数である。
curve(dgamma(x, shape=5, scale=4),0,100)
ガンマ分布に従う確率変数の期待値は $k\theta$ である。上図の例では、5×4=20 に全体の平均がある。
モデリング
航空会社の効果を入れた一般化線形モデルを以下のように構築する。
- 線形予測子 $z_i=w_0+(w_1;w_2;w_3;w_4)\boldsymbol{\delta}_i$
- リンク関数 $\log(k\theta_i)=z_i$
- 確率分布 $x_i \sim \text{Gamma}(k,\theta_i)$
$\boldsymbol{\delta_i}$ は、 $i$ 番目の例の航空会社(MQ, DL, 9E, EV)を表すone-hotベクトルである。 $\delta_{i1}=1-\delta_{i2}-\delta_{i3}-\delta_{i4}$ であることに注意して線形予測式を書き直すと
\begin{aligned}
z_i&=(w_0+w_1)+(w_2-w_1)\delta_{i2}+(w_3-w_1)\delta_{i3}+(w_4-w_1)\delta_{i4} \\
&=w'_0+w'_2\delta_{i2}+w'_3\delta_{i3}+w'_4\delta_{i4} \\
&=\begin{cases}
w'_0 \quad \text{(if $\delta_{i1}=1$)} \\
w'_0+w'_j \quad \text{(if $\delta_{ij}=1$ for $j\neq1$)} \end{cases}
\end{aligned}
リンク関数として log を指定したが、別に恒等関数でもいい。log にすると、平均 $k\theta_i$ が必ず正になるので、時間のモデル化には少し気分がいいというほどのものである。
一方、航空会社の効果を検証するためのnullモデルでは、線形予測子は $z_i=w_0$ (定数)である。
GLMによる分析
航空会社を説明変数に入れたモデル
上で述べたモデリングをRで記述すると以下のようになる。
(fit.glm <- glm(relativetime ~ carrier,
family = Gamma(link = "log"),
data = data))
Call: glm(formula = relativetime ~ carrier, family = Gamma(link = "log"),
data = data)
Coefficients:
(Intercept) carrierDL carrier9E carrierEV
2.94583 -0.07043 0.24602 -0.21716
Degrees of Freedom: 4906 Total (i.e. Null); 4903 Residual
Null Deviance: 893.1
Residual Deviance: 886.6 AIC: 33280
$w'_0=2.945$, $w'_2=-0.070$, $w'_3=0.246$, $w'_4=-0.217$ と推定された。
AICは33280となった。
モデリングの節に書いた式から、航空会社がDL ($j=2$) の場合には $$k\theta_i=\exp(z_i)=\exp(w'_0+w'_2)$$
となる。平均 $k\theta$ を求めると
(ktheta <- exp(sum(fit.glm$coefficients[c(1,2)])))
[1] 17.73254
一方、推定された $k$ (shapeパラメータ) は
library(MASS)
(k <- gamma.shape(fit.glm)$alpha)
[1] 5.696083
これより $\theta=(k\theta)/k$ は次のように求められる。
(theta <- ktheta / k)
[1] 3.113112
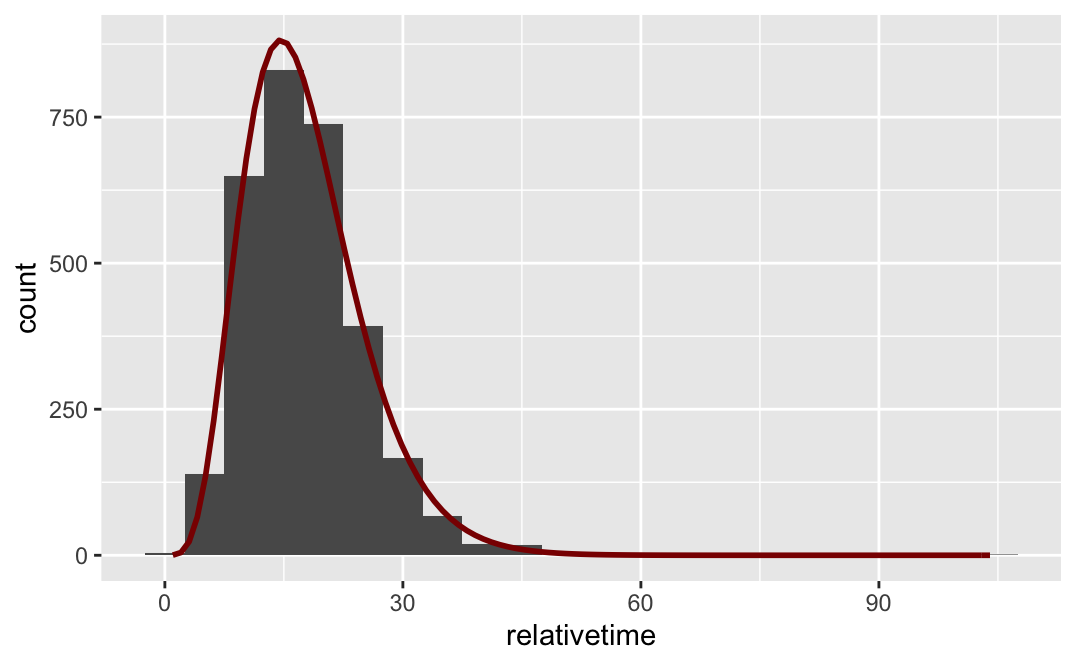
DLに対して推定されたガンマ分布をヒストグラムと重ねてみよう。
binw <- 5
data %>%
filter(carrier=="DL") %>%
nrow() -> ndata
data %>%
filter(carrier=="DL") %>%
ggplot() +
geom_histogram(aes(x=relativetime),binwidth=binw) +
stat_function(fun=function(x) dgamma(x,shape=k,scale=theta)*ndata*binw,color="darkred",size=1)
Nullモデルとの比較
(glm(relativetime ~ 1,
family = Gamma(link = "log"),
data = data))
Call: glm(formula = relativetime ~ 1, family = Gamma(link = "log"),
data = data)
Coefficients:
(Intercept)
2.902
Degrees of Freedom: 4906 Total (i.e. Null); 4906 Residual
Null Deviance: 893.1
Residual Deviance: 893.1 AIC: 33310
Nullモデルの場合、AICは33310となった。航空会社を説明変数に入れたモデルの方がAICが小さいので、航空会社によって時間に差があると言える。
多重比較
多重比較を行うためには、(MQ, DL, 9E, EV)のグルーピングの可能性を全て列挙する必要がある。ここでは partitions パッケージを用いる。
library(partitions)
listParts関数を使うと、4つの要素のグルーピングの可能性を全て列挙する。
listParts(4)
[[1]]
[1] (1,2,3,4)
[[2]]
[1] (1,2,4)(3)
[[3]]
[1] (1,2,3)(4)
[[4]]
[1] (1,3,4)(2)
[[5]]
[1] (2,3,4)(1)
[[6]]
[1] (1,4)(2,3)
[[7]]
[1] (1,2)(3,4)
[[8]]
[1] (1,3)(2,4)
[[9]]
[1] (1,4)(2)(3)
[[10]]
[1] (1,2)(3)(4)
[[11]]
[1] (1,3)(2)(4)
[[12]]
[1] (2,4)(1)(3)
[[13]]
[1] (2,3)(1)(4)
[[14]]
[1] (3,4)(1)(2)
[[15]]
[1] (1)(2)(3)(4)
全部で15通りあることがわかる。
setparts関数を使うと、この15通りのそれぞれで、各航空会社が何番目のグループに入るかがわかる。これを利用して、各便が何番目のグループであるかを表わす subgr 列を追加する。
次に、グループを説明変数として GLM のパラメータを推定する。
以上を、15通り全てに対して実行し、AICが最小となったモデルを求める。
library(partitions)
carriers <- levels(data$carrier)
glm4apartition <- function(partno) {
apartition <- setparts(length(carriers))[,partno]
data %>%
mutate(subgr = as_factor(apartition[carrier])) -> tmp
list(partition=partno,
model=glm(relativetime ~ subgr,
family = Gamma(link = "log"),
data = tmp))
}
carriersubsets <- listParts(length(carriers))
partseq <- 2:length(carriersubsets) # 1は全体が1グループなのでsubgrを説明変数にできない
result <- map(partseq, glm4apartition)
bestresult <- result[[which.min(map(result,function(ap) ap[[2]]$aic))]]
carriersubsets[bestresult$partition]
(bestmodel <- bestresult$model)
[[1]]
[1] (1,3)(2,4)
Call: glm(formula = relativetime ~ subgr, family = Gamma(link = "log"),
data = tmp)
Coefficients:
(Intercept) subgr2
2.9463 -0.0716
Degrees of Freedom: 4906 Total (i.e. Null); 4905 Residual
Null Deviance: 893.1
Residual Deviance: 887.1 AIC: 33280
最適なグルーピングは (1,3)(2,4) すなわちMQと9Eを同じグループ、DLとEVを同じグループとみなしたモデルが最良であった。
このことから、9E = MQ > DL = EV と結論できる。単純な平均の比較では 9E > MQ > DL > EV であったが、一部の群間には差はなさそうだということがわかった。