はじめに
マイクロサービスアーキテクチャは、独立してデプロイ可能で疎結合サブシステム群によってサービス開発を行うというアーキテクチャパターンです。現在のソフトウェアサービス開発では欠かすことができない考え方です。
従来では一定のコストが掛かり、またパフォーマンス上の問題もあったため、必要に応じての分割には難しい側面も多かったのですが、様々なエコシステムの発達によってわずかな機会費用で実現できるようになってきました。もちろん分散システムとしての本質的な難しさやアーキテクチャの移行の本質的な難しさは解決したわけではありませんが、手軽にコンテナレベルで分割された様々なサービスを作成することのコストは急速に下がってきました。
これらが、うまくサブドメイン境界によって分割されることで、ある開発チームが知らなければならない情報が制限されるため、スピード感のある開発力を維持しながら開発組織のスケールできるようになるため、コンウェイの法則や逆コンウェイ戦略というアプローチともフィットし、技術組織とマイクロサービスアーキテクチャは切ってもきれない関係があります。
今回は、どのような粒度でマイクロサービスを分割することが適切なのか。そして、それはどのようにしてモニタリングできるのだろうかということを、簡素化した数理モデルをつくって理解できるのではないかという思考実験の内容をご紹介します。
この思考実験の結果としては、さまざまな単純化した仮定を置けば
- アーキテクチャの適応度
- アーキテクチャの経済的価値
の関係性がモデル化ができることを示します。また、それによって、「アーキテクチャ適応度」を具体的に計測する方法として、「直近または将来のタスクが"いくつのサービス修正によって実現できるのか"」という数列から推論できることも応用範囲としては面白い結果になるかとおもいます。
前提とマイクロサービス議論の噛み合わなさ
かつては、ネットワーク越しのサービスとして異なるモジュールを作ることの実装上、パフォーマンス上のコストは高かったため:
このモジュール化粒度が:
実装上のサービス単位 > 開発チームの認知限界 > サブドメイン境界
という関係でありました。モノリス化されたサービスの開発が技術的負債になりやすく開発速度の低下を招きがちだったため、モノリスからマイクロサービスへの分割をしようとする開発企業が増えてきました。
たとえば、開発チームの認知限界をおおよそ20-100万行程度とみなしたときに、それを超えない程度のサブドメイン境界で分割しようという試みです。
より大幅に規模の大きいエンタープライズアーキテクチャであっても、おおよそ1MSLoC程度では分割されたサブシステムとして実現されることが多いです。(これは組織チームだけでなく、開発ベンダーの境界になっている場合もある)
一方で、サービス分割の技術的な面での機会費用が限りなく小さくなってきた現在において、ゼロからマイクロサービスアーキテクチャとして実装されている仕組みでは、より小さい単位で分割することが多いかと思います。
そのため:
開発チームの認知限界 > サブドメイン境界 > 実装上のサービス単位
となっていることも多く、たとえば、5000行-2万行程度のサービスを5-10個、同じチームの人間が改善していたりもします。これだけ独立したサブシステムの開発が容易になったため、自明に疎結合な実装が適したものに関しては迷わずに独立したサブシステムにしても良いということは適切な判断であると言えるでしょう。
ところが、この両者は随分と1サービスに求めるものが違うため
- 技術的異質性
- 実チームとの紐付け
- リポジトリの分割
- 自動テスティング
- APIスキーマ・クオータ管理
をどの程度すべきかなどの様々な点で論点が噛み合わなかったりします。どちらの主張も自然であっても規模が違うと見え方が違ったりします。
今回は、モジュール分割の経済合理性についてを論点としたいので、ビジネスケイパビリティによる分散統治が実現され、認知限界を超えないサブドメイン境界の単位を1つのサービスコンポーネントとして捉える(つまり、実装上マイクロサービス分割されていても、複数のサービス間がタスクベースで密結合であれば1つのモジュールとしてとらえる)前提で議論を展開していければと思います。
分割オプションの価値とコーディネーションコスト
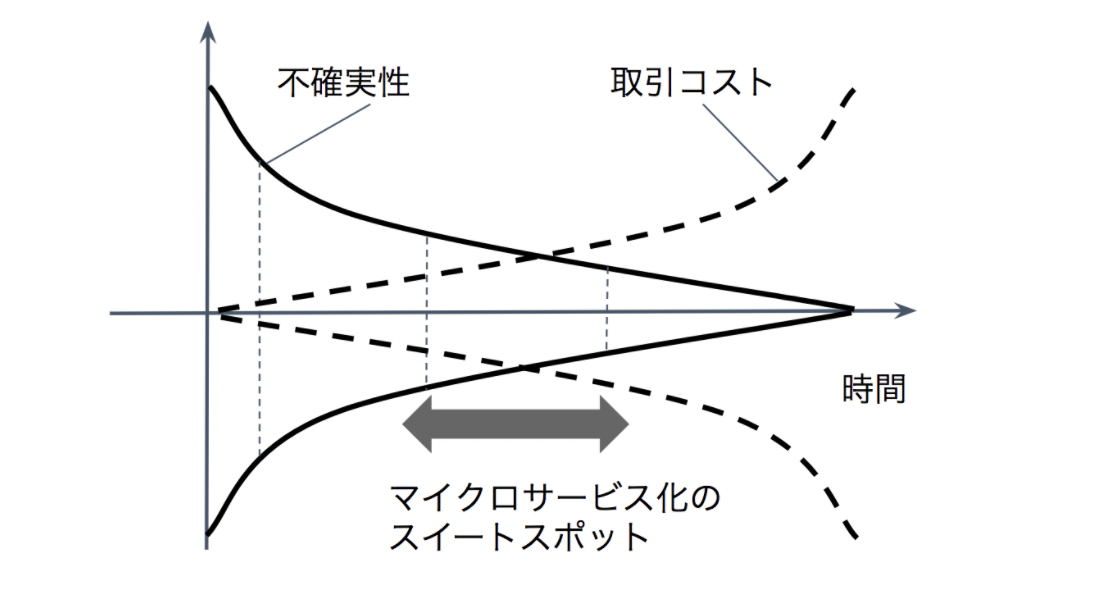
一般的なマイクロサービスアーキテクチャの説明として、疎結合なシステムに分解されることによってチームは独立して改善を行うことができ、それによって開発速度を維持しながら事業開発ができるという利点が挙げられます。このような利点を金銭的価値に変換するとしたら、リアルオプション価値としてとらえることができるでしょう。このようなアーキテクチャ分割のオプション価値について検討してきたいと思います。
もし、サービスを分解すればするほど価値が上がるのであれば、サービスは機械語の単位で分割したら価値が最大化するということになってしまう。技術的なコストの問題ももちろんあるんですが、開発効率においてもどこかでサチュレートするような関数になるでしょう。これを分割オプションの価値関数と捉えましょう。
また、もう一方の観点として、独立した改善ができずに複数のサービスの間でタスクをこなすという場合も現実的には発生します。このようなケースには、結局は調整のコストが掛かります。このようコーディネーションコストに関しても、n個のサービスが修正するのであれば$n(n-1)/2$のオーダーで発生するでしょう。これを調整コスト関数として捉えましょう。模式的な図を用意すると

分割数が上昇すると、一定のところまでは価値が増え続けるが、調整コストの増大がそれを追い抜いてしまうということが考えられます。この価値と調整コストの差が最大となるところが適切な分割数ということができるのではないでしょうか。このぞれぞれ分割オプション価値の関数と調整コストの関数についてより単純化をしながらモデルを考えてみましょう。
"分割オプション価値"をアムダールの法則から考える。
アムダールの法則は、並列計算を行うコンピュータが並列度を上げた場合に、並列化できない部分の割合がボトルネックとなることを示したものです。
あるタスクが並列実行できる部分が全体の8割で、残りの2割は並列実行できないとします。このとき、S個のプロセッサで並列処理する場合を考えると全体のパフォーマンス効率は1個のプロセッサで処理する場合に比べて以下のように表現できます。
{\frac {1}{(1-P)+{\frac {P}{S}}}}
たとえば、プロセッサが4個であれば、$1/(0.2 + (0.8/4)) = 2.5$で、1つの場合に比べて4倍よりも小さい値になっています。仮にプロセッサの数が無限個あったとしても、$\lim_{S \to \infty}0.8/S=0$になるだけなので、たかだか5倍までしか高速化ができないことがわかります。
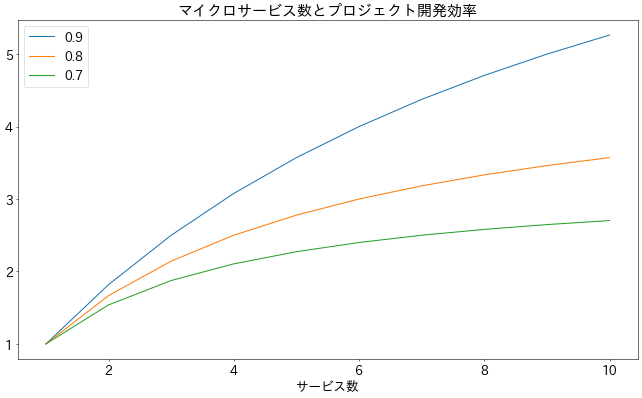
このような主張がアムダールの法則です。これをマイクロサービス環境下におけるソフトウェア開発のチーム開発に応用してみると、このような図が作成できます。
1-10個程度までのドメインの中にやってくるタスクの9割が並列で実行できるタスクがあれば、5倍程度にまで開発効率が上がります。
この開発効率をそのままリアルオプション的な経済価値として捉えると(タスクの大きさが一定で、成否の確率が同程度であった場合、価値はタスク数に比例すると考えることができる)、この並列で仕事をできる割合が判明すれば、マイクロサービス化の経済的な価値を説明できることになります。極めて単純化されたモデルではありますが。
タスクベースと設計ベースの依存関係
またここで補助線として、タスクベースの依存関係について考えてみます。あるタスク(追加機能と考えていいです)を実施するにあたって、複数のサービスの修正をしなければならないことがあります。たとえば、APIサーバーを修正したらかならずBFFを修正しなければならないなどです。これは設計ベースの依存関係とは別で、設計的には依存していてもBFFだけを修正するタスクやAPIサーバーだけを修正するタスクというものは存在します。
このような"タスクベースの依存関係"は、構築する機能がわからないと決まりません。構築する機能は、ユーザーのニーズや外部環境などの不確実性がありますから、予め全てがわかるわけではありません。
これらの将来にわたってのタスクのリストを考えると、
T = [T1,T2,T3 ...] = [\{s1,s2\},\{s1\},\{s3,s2\},...]
のように修正が必要になるサービスの集合のリストとして考えることができます。これらの同時に現れる確率などを考えると、タスクベースの依存関係マップをデザイン構造行列などに表すこともできるでしょうが、ここではその議論は割愛して、純粋に個数にだけ注目します。
Num(T)= [Num(T1),Num(T2),Num(T3),...] = [2,1,2...]
というタスクリストを考えます。この数が少ないほど、タスクを実装するのに改修しなければならないサービスは少なくなります。マイクロサービスの価値は、改善がうまくいくいかないにせよ独立した改善が可能であるというオプション価値によって生まれますから、数が少なくて済むのであれば良いアーキテクチャと言えるかもしれません。
ここで、$Num(T)$が、二項分布に従うと仮定してみます。N個のサービスがあれば、そのうちどれもが確率pで選ばれるということです。必ず1つは関連するサービスがあり、残りをN-1個から選ぶと考えましょう。
def task_list(N=10,P=0.1) :
return np.random.binomial(N-1,P,size=100)+1
task_list()
# array([1, 3, 4, 1, 4, 1, 1, 2, 2, 3, 4, 2, 2, 1, 3, 2, 2, 3, 2, 3, 2, 3,
# 2, 1, 1, 3, 2, 1, 2, 2, 1, 3, 2, 2, 2, 2, 2, 2, 2, 5, 1, 1, 1, 2,
# 2, 1, 1, 1, 2, 4, 2, 2, 3, 2, 2, 2, 3, 1, 1, 3, 4, 1, 2, 1, 2, 4,
# 1, 2, 3, 2, 3, 1, 2, 2, 1, 1, 3, 2, 1, 3, 1, 2, 1, 1, 1, 2, 1, 1,
# 2, 3, 2, 4, 3, 1, 1, 1, 1, 2, 2, 2])
たとえば、サービス数が30個、確率$p$が$0.05,0.2,0.4$のときの分布を見てみましょう。
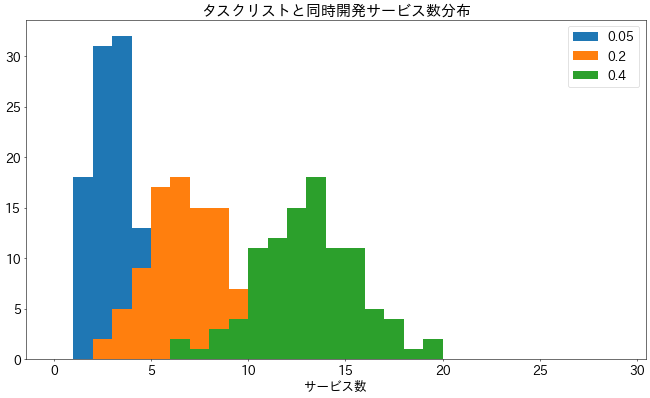
$p$が小さいほど、1つのタスクで同時に修正しなければならないサービスが少なくなることがわかります。
二項分布の期待値は
E[X] = np
となるので、単純に10個のサービスのとき、$p=0.1$であれば平均は、$E[X]=(N-1)p+1=1.9$個となります。この性質を仮定すると、実際のタスクリストと関連サービスの数から確率pを推定することができます。
この確率$p$に対して、$1-p$を$アーキテクチャ適応度q$とすると、
T = [1,1,2,2,1,1,2] # 直近のタスク列
N = 5 # 5個分割
1-(np.average(T)-1)/(N-1)
# 0.892 (アーキテクチャ適応度)
と求めることができます。
次にアーキテクチャ適応度に対して、タスク実装のために必要なコーディネーションコストがどのように変化するのかを考えてみます。
複数のサービスにまたがった開発をするにあたっての総コストを定義します。
まず、純粋にタスクをこなすのに必要なコストと、複数のサービス間の調整を行う必要があるコストを考えてみます。この総和が、あるタスクをこなすのに必要な総コストだと定義します。
総コスト = 調整コストC + 純タスクコストE
複数のサービス間の調整コストは、そのコミュニケーションチャネルの数だけ必要だと仮定します。そうすると、$n(n-1)/2$だけのコストがかかりえます。1/2は係数$C_0$に押し込めて、調整コストを定義するとあるタスク列$T$のi番目のタスクコストは
Cost_i = t_i( t_i -1 )C_0 + E
と定義できます。
ここに平均サービス数は$(N-1)p+1$ですから、代入したものが平均コストになります。
def cordination_cost(P,N,C) :
t = (N-1)*P+1
return t * (t-1) *C
def estimate_cost(P=0.1,N=10,C=0.1,E=3.0) :
return cordination_cost(P,N,C) + E
x = [ 0.01 * p for p in range(100) ]
q = -np.array(x)+1
y = [ estimate_cost(P=p) for p in x ]
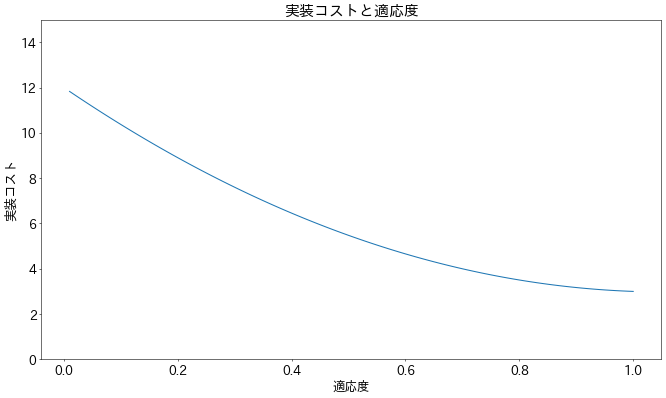
サービス数$N=10$、調整コスト係数$C_0=0.1$、実装コスト$E = 3.0$と置くと適応度に対して、以下のようなグラフが得られます。適応度の低いアーキテクチャは、実装におけるコストが最大4倍程度かかることが見て取れます。
利得が最大になる"分割数"はどうなるか
ここまでの仮定をもとに冒頭のモデルを軸に適切な分割数を考えてみます。
適応度に関するコストのグラフと、その適応度の時の調整コストと実装コストの比をアムダールの法則で計算したものを比べてみます。効率と価値の変換係数をOとしておいています。
V = Amdahl(E/(c+E),N) \times O
コードは以下:
def option_value(P = 0.1 , N = 10 , C = 0.1 , E=3.0, O= 1.0) :
c = cordination_cost(P=P,N=N,C=C)
r = E/(c+E) # コーディネーションコストと実装コストの比率
return amdahl(ratio=r,num=N) *O
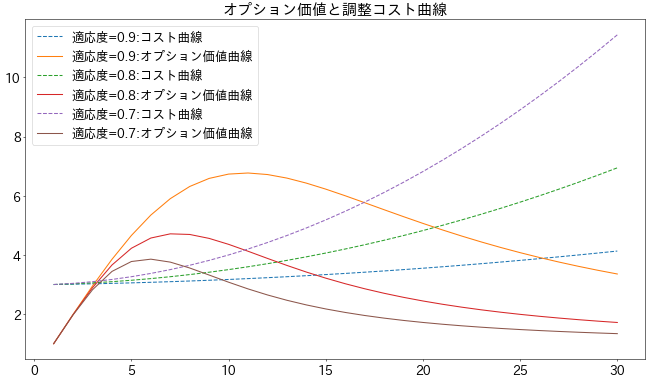
これをもとにコスト関数とオプション価値関数を比べてみます。
x = np.linspace(1,30,num=30)
for q in [0.9,0.8,0.7] :
plt.plot(x,estimate_cost(P=1-q,N=x),label=f'適応度={q}:コスト曲線',linestyle="dashed")
plt.plot(x,option_value(P=1-q,N=x),label=f'適応度={q}:オプション価値曲線')
plt.legend()
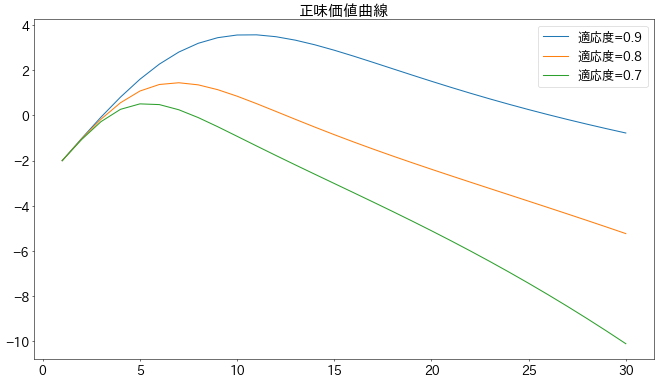
オプション価値からコストを引いたものを正味オプション価値としたときのグラフです。
このモデルの係数では、適応度0.9のときには10分割程度が経済的合理性があるようです。
おわりに
これまでに述べたモデルは、単純化した仮定の上に成り立っています。しかし、適応度が低いマイクロサービスアーキテクチャであれば、価値が低く分割をする意味がなかったり、無駄が多くなってしまうことが見て取れます。
では、適応度が高いマイクロサービス分割はどのようなタイミングできるかと言うと、事業において作るものの不確実性が低く、相応な事前コストを支払えるときになります。
取引コストとオプション価値に注目することでマイクロサービス設計と組織設計における議論が進展することを願っています。