この記事は MicroAd (マイクロアド) Advent Calendar 2019の13日目の記事です。
内容について
当初は、禁止位置のある組合せ順列の総数を計算する、という内容で書こうとしてましたが、代わりに「メビウス関数の値を計算して包除原理とメビウス変換を理解する」というような内容を書きます。内容が大きく異なってしまったのですが、WEBで完全順列の一般化やら包除原理について検索している際に出会った「高速ゼータ変換・高速メビウス変換」というコード断片(競技プログラミング向けのコード)に関する説明が理解できずに、脱線して時間を浪費してしまいました。そのメビウス変換と包除原理の関係を理解するために調べたことを書きます。
アルゴリズムの説明が理解できない
最初は、「高速ゼータ変換 メビウス変換」などで検索して説明を読んでもアルゴリズムがいまいち理解できませんでした。そのため、単純なケースに絞って「高速ゼータ変換 累積和」のようにして検索したり、また以下のサイトを読んだりしました。
https://lumakernel.github.io/ecasdqina/algorithm/FastZetaTransform
上記サイトに、メビウスの反転公式について一言ありますが、ここから復習したのが脱線の始まりでした。復習の際は以下の本
https://www.oreilly.co.jp/books/9784873114057/
のp280あたりを見て、次のような記述を読みました。
メビウス関数は包除定理を符号化するのにとても便利だ。
この本でこの直後に古典的な(数論での)メビウス関数の値が具体的に書かれていますが、あまりピンとこなかったです。そこでさらに情報を集めました。ここで、以下のプレプリントPDF(ec1.pdf)でMöbius inversionを勉強すべく p277 を参照したと思いますが、このあとp303あたりにも話が出てくるのですが、内容が理解できず勉強を続けました。
http://www-math.mit.edu/~rstan/ec/ec1.pdf
包除原理を順序理論で考える
「半順序集合、束(lattice)、隣接代数 (順序理論)」などいろいろ調べた気がしますが、包除原理を考えるときに、順序集合やら束という概念を使って、順序集合論でいうところのゼータ関数とメビウス関数というのを定義すると大変見通しが良いことが分かってきました。それについて書いてみます。
ゼータ関数とメビウス関数
最初に、通常の自然数のもつ順序の性質(順序構造)を使って、順序集合論のゼータ関数というものを定義してみます。最初は例で考えたほうが早いので、行列を用いて累積和を作ってみます。
ここでは、累積和$S_n$が数列$a_n$で以下のように定義されているとします。
S_1 = a_1 \\
S_2 = a_1 + a_2 \\
\cdots \\
S_n = a_1 + a_2 + \cdots + a_n
このとき以下のような簡単な行列を考えることが可能です。
(S_1,S_2,\cdots,S_n) =
(a_1,a_2,\cdots,a_n)
\left(
\begin{array}{ccccc} 1 & \cdots & 1 & \cdots & 1 \\
\vdots & \ddots & & & \vdots \\
0 & & 1 & & 1 \\
\vdots & & & \ddots & \vdots \\
0 & \cdots & 0 & \cdots & 1
\end{array}
\right) \qquad (1) \\
上の式から$S_n - S_{n-1} = a_n$ のような式を作り累積和を計算する手法を競技プログラミング界隈ではゼータ変換の一種として呼ばれているようで、コード断片が出回っています。これを数式で表現したのが順序集合論で定義される次のゼータ関数となります。
定義は
\zeta(x,y) = \left\{
\begin{array}{ll}
1 & (x \leq y) \\
0 & (other)
\end{array}
\right.
式(1)の右辺の nxn行列をAとすると、$\zeta(x,y)$ はAの定義が以下であることに対応しています。
A = (a_{ij}); \quad a_{ij} = \left\{
\begin{array}{ll}
1 & (i \leq j) \\
0 & (i \gt j)
\end{array}
\right.
一方、上記のように、$\zeta(x,y)$ を行列表示したもの行列Aの逆行列(逆元)が順序集合論でいうところのメビウス関数に対応します。これも一緒にコード断片が出回っている(高速)メビウス変換に関連する関数です。最初、行列を例に使いましたが、行列表示が便利なのは自然数や整除関係(同様の考えで$a_{ij}$を考えると行列表示可能)といった特定の構造に限られてしまうので、ここでは包除原理を考えるために、一般的なメビウス関数を定義して使いたいと思います。これは以下のように帰納的な定義式になります。
\mu(x,y) = \left\{
\begin{array}{ll}
1 & (x=y) \\
- \sum_{z:x≦z<y} \mu(x,z) & (x \lt y) \quad (2) \\
- \sum_{z:x<z≦y} \mu(z,y) & (x \lt y) \quad (3) \\
0 & (other)
\end{array}
\right.
この式を「帰納的な定義」として以下で使います。なお、逆元としての性質をきちんと考える際はここに記載されているデルタ函数$\delta$を使って反転公式を証明したりするのですが、ここでは割愛します(リンクを貼っておきます)。
メビウスの反転公式の一般化された定義式へのリンクですが、
https://en.wikipedia.org/wiki/M%C3%B6bius_inversion_formula#On_posets
とここの
(See Stanley's Enumerative Combinatorics, Vol 1, Section 3.7.)
とある以下のプレプリント版
http://www-math.mit.edu/~rstan/ec/ec1.pdf
の p303 の3.7.1 Proposition と 3.7.2 Proposition の dual form のところを主に参考にしました。
pdfに定義が2種類あり、反転公式に登場する式としては計4つあります。ブログでよく見かける4つの式がこれです。ゼータとメビウスがそれぞれ集合の順序関係(包含関係)の上位集合と下位集合に対して定義します。
定義関係はこれくらいにして、以下では構造毎にメビウス関数を考えて理解を深めたいと思います。自然数や約数や集合の包含関係など、代表的な順序構造を挙げてあります。
自然数
自然数は全順序構造なのでメビウス関数を考えることは可能です。上で行列の例がそれです。この場合、メビウスの反転公式は以下のようになります。fのゼータ変換gはfの累積和です。fをgで表したのがメビウス変換に相当しますが、$f(n)$のところで数列の階差の形が現れており、上の$S_n$が$g(n)$に対応します(この反転の式から積分や微分と対応させて考える話もあります)。
g(n) = \sum_{x≦n} f(x) \\
f(n) = \sum_{x≦n} \mu(x,y)g(x) = g(n+1) - g(n)
整除関係
順序の構造が整除関係のときは、メビウス関数は数論でお馴染みの次の定義で表せます(このお馴染みの式のほうが古いので帰納的な定義のほうがのちの拡張という言い方が正しいですが)。このあたりに書かれている性質があります。
\mu(n) = \left\{
\begin{array}{ll}
0 & (n が平方因子を持つとき) \\
(-1)^k & (n が相異なる k 個の素因数に分解されるとき ※)
\end{array}
\right.
※ 但し
- n が相異なる偶数個の素数の積からなる square-free な正の整数であれば μ(n) = 1
- n が相異なる奇数個の素数の積からなる square-free な正の整数であれば μ(n) = -1
のような定義になります。帰納的な定義よりは使いやすいです。 square-free という性質の逆で、squared であれば0になるという性質がよく使われると思います。自然数の和を考える時、無視できる部分となるので、アルゴリズムを考える時によく登場すると思います。半順序集合で定義されたメビウス関数として考える際は$\mu(n) = \mu(n, 1)$ のようなルールを導入すると古典的なメビウス関数と1:1に対応します。
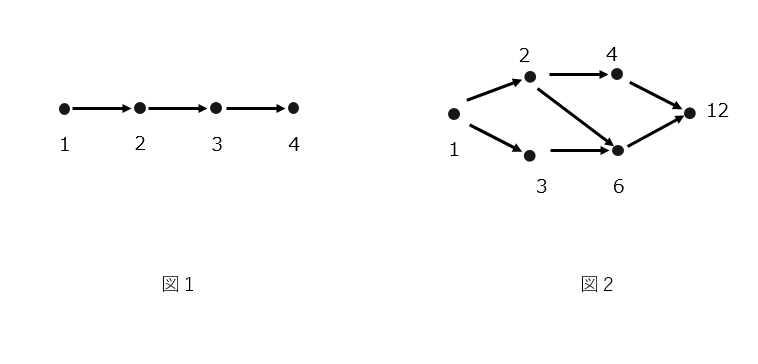
下の表は図1,2の自然数と整除関係(約数関係)の$\mu$の値を計算したものです。自然数は常に開始点とその隣だけ見ればよく、その結果、$g(n+1)-g(n)$のように階差の式として表現できます。整除関係のほうは計算の途中を具体的に書いてみます。
| 1 | 2 | 3 | 4 | 6 | 12 | ||
|---|---|---|---|---|---|---|---|
| 図1 | 全順序(自然数) | 1 | -1 | 0 | 0 | - | - |
| 図2 | 整除関係 | 1 | -1 | -1 | 0 | 1 | 0 |
図2の整除関係の計算ですが、帰納的な定義を用いて、
\mu(1,1)= 1 \\
\mu(1,2)= -\mu(1,1) = -1 \\
\mu(1,3)= -\mu(1,1) = -1 \\
\mu(1,4)= -\mu(1,1) -\mu(1,2) = -1 -(-1) = 0 \\
\mu(1,6)= -\mu(1,1) -\mu(1,2) -\mu(1,3) = -1 -(-1) -(-1) = 1\\
\mu(1,12)=-\mu(1,1) -\mu(1,2) -\mu(1,3) -\mu(1,6)= -1 -(-1) -(-1) -1 = 0
のような計算になっています。
包含関係
順序の構造が包含関係になっているものが、包除原理であり、これをメビウス関数で理解するのがこの記事の目的でした。ここでは、任意の集合 A に対して、A の冪集合(A の部分集合全体からなる族)$B_n$ を考えます。
この冪集合$B_n$に対して、メビウス関数を定義すると
\mu_{B_n}(S,T) = (-1)^{|T|-|S|} \quad (4)
になります。帰納的な定義と比べて非常に使いやすいです。このような簡単な式になるのは、べき集合の持つ構造がシンプルだからです(冪集合$B_n$の元の個数は$2^n$ですが、この辺の性質やら順序集合論の直積やらを用いて、関数がシンプルに表現できることを証明するようです)。反転公式は上で書いた高速ゼータ変換と高速メビウス変換がまさにその例であり、重要な4つの式が出ます。
ここではシンプルな構造を具体的に見ておきます。
ここでは、ec1.pdfのp277(p303,304)の(3.1)の例を使います。
今、次のような集合A,B,C(,D, $\hat{1}$ )
A = \{a,d\} \quad B = \{b,d\} \quad C = \{c,d\} \\
D = \{d\} \quad \hat{1} = \{a,b,c,d\}
の3(+2)の集合があって、$A \cap B =B \cap C =C \cap A = A \cap B \cap C \quad(= D) $
が成り立っているとします。$\hat{1}$ は包含関係がつくる順序集合の最大元としてよく使う表現で、同様に、$\hat{0}$は最小元で使われます。集合Aの冪集合$B_n$の場合、A自身が最大元で、$\phi$が最小元となります。ここで、$B_n$の例として$B_4$、さらに、このA,B,Cの構造を考えます。$B_4$は{A,B,C,D}の冪集合です。
| 5階 | 4階 | 3階 | 2階 | 1階 | ||
|---|---|---|---|---|---|---|
| 図3 | 冪集合$B_4$ | 1 | 4 | 6 | 4 | 1 |
| 図4 | 集合A,B,C,D | 1 | 0 | 3 | 1 | 0 |
上の図3は$B_4$のハッセ図の構造の形のみ抽出しています(実は書きかけの図を使っている)。図4は図3のうち、黄色い部分のみ集合を考えたものです。表は図3,4の構造を横で区切って階に見立て、各々で要素数をまとめたものです。諸事情により画像が編集できないPCで記事を書いており、(重々承知の上)まどろっこしい説明をします。
from functools import partial
from itertools import combinations
def gen_powerset(n, x):
return combinations(n, x)
n = 'ABCD'
B_n = partial(gen_powerset, n)
print("B_4(Fig3):")
for x in range(len(n),-1,-1):
e = [set(i) for i in B_n(x)]
print(len(e), e)
print("\nABCD(Fig4):")
max_elm = [set('ABCD')]
elements = [set('A'),set('B'),set('C')]
min_elm = [set('D')]
for e in [max_elm, elements, min_elm]:
print(len(e), e)
このコードの実行結果です。
| 数(図3) | 集合の族(図3) | 数(図4) | 集合の族(図4) |
|---|---|---|---|
| 1 | [{'A', 'B', 'D', 'C'}] | 1 | [{'A', 'B', 'D', 'C'}] |
| 4 | [{'A', 'B', 'C'}, {'A', 'B', 'D'}, {'A', 'C', 'D'}, {'B', 'D', 'C'}] | 3 | [{'A'}, {'B'}, {'C'}] |
| 6 | [{'A', 'B'}, {'A', 'C'}, {'A', 'D'}, {'B', 'C'}, {'B', 'D'}, {'C', 'D'}] | 1 | [{'D'}] |
| 4 | [{'A'}, {'B'}, {'C'}, {'D'}] | - | - |
| 1 | [set()] | - | - |
図3の構造は次のようになっています(数が多いので階で整理)。
| 5階 | 4階 | 3階 | 2階 | 1階 | |
|---|---|---|---|---|---|
| 冪集合$B_4$ | 1 | 4 | 6 | 4 | 1 |
| $\mu(x,y)$ | 1 | -1 | 1 | -1 | 1 |
このように、$B_4$は$\phi$から各集合への順序を(2)のμ(0^,y)として計算すると階毎に{1,-1}を繰り返します((3)のμ(x,1^)を用いると符号が反転する)。
一方、図4の構造は冪集合ではない単なる包含関係の構造なので、次のようになっています(μは(3)を用いた)。
| #T | T | f(T) | g(T) | $\mu(x,y)$ |
|:-:|:-:|:-:|:-:|:-: |:-: |
| 4 | 1^ = {a,b,c,d} | 0 | f(D)+f(A)+f(B)+f(C)+f(1) | 1 |
| 2 | {a,d} | 1 | f(D)+f(A) | -1 = μ(A,1^) |
| 2 | {b,d} | 1 | f(D)+f(B) | -1 = μ(B,1^) |
| 2 | {c,d} | 1 | f(D)+f(C) | -1 = μ(C,1^) |
| 1 | {d} | 1 | f(D) | 2 = μ(D,1^) |
次に、図4の集合ABCDについて、包除原理のような式を用いて計算します。7項の式から4つの項に縮まる際には係数に上の表の$\mu(x,y)$ の値が使われています。
| \{a,b,c,d\} | = |A \cup B \cup C| \\
= |A| + |B| + |C|
-|A \cap B|
-|A \cap C|
-|B \cap C|
+|A \cap B\cap C| \\
= |A|+|B|+|C|-2|D|
帰納的な定義式(2)や(3)を用いて計算すると、順序関係がつくる依存関係(ハッセ図で現れる線)によってメビウス関数の値が変化します。図4の集合ABCDとは違い、冪集合のような構造はメビウス関数の値が{1,-1}しか登場しないため、容易に計算が可能です。
以上、$B_4$を使って説明してきましたが、(4)式との対応付けを書きます。
| $B_4$ | (4)式 |
|---|---|
| $\phi$ | S |
| $ \{a\} $ | $ \{a\} \cup S$ |
| $ \{b\} $ | $ \{b\} \cup S$ |
| $\cdots$ | $\cdots$ |
| $ \{a,b\} $ | $ \{a,b\} \cup S$ |
| $\cdots$ | $\cdots$ |
| $ \{a,b,c,d\} $ | T = $ \{a,b,c,d\} \cup S$ |
反転公式で使ってきたf, gを使って包除原理の式を書くと次のようになります。
g(T) = \sum_{S≦T} f(S) \\
f(T) = \sum_{S≦T} \mu_{Bn}(S,T)g(S) = \sum_{S≦T} (-1)^{|T|-|S|}g(S)
その他(分割の細分)
四元集合 {1,2,3,4} の分割の成す束の例がこの束論 のページに図示されています。この A={1,2,3,4} の分割全体の成す族に分割の細分によって順序を入れたものを考えて、最小元 1/2/3/4 から最大元 1234 へのメビウス関数の値を計算すると-6になります。分割の細分については包含関係と同様に陽に定義された式もある(このPartitions of a setの箇所)のですが、他の複雑な構造の場合、(半)順序集合の上で順序に従って帰納的に行う方法が唯一の計算方法です(式が知られていないためExcelなどで計算します)。
最後に
以上まで理解した段階で、アルゴリズム(コード断片)の方の高速ゼータ変換と高速メビウス変換の説明がしっくり来るようになりました。説明が抜けている箇所も多いと思いますが、メビウス関数の帰納的な定義から出発して、整除関係や包含関係でよく見る公式が出てくるのは面白いです。ただ、帰納的な定義はあまり使いやすいものではないので、直接は使わないかもしれません。競技プログラミングでコードを書くときに整除関係で実際使う知識と包含関係で実際使う知識は全然別なのは当たり前なのですが、こういった隣接代数のさわりの話を知っておくと、バラバラの知識を整理するときに多少役立つと思います。