【特訓 ver.3】 重回帰スタート！！
※この記事では重回帰分析と標準化についてまとめます
▼学習の流れ
まずは、大まかな流れを抑える
■使用するデータ
お弁当の販売数に関するデータを用いる
※データセット： https://signate.jp/competitions/24/data
■ 単回帰分析
復習のため最後の精度確認のみ添付
（残差プロット、MSE、決定係数）
※参照：単回帰まとめデータ
https://qiita.com/hirohiro18/items/d8a14915c6789a79b56d
■ 重回帰分析について学習する
注意点）
① データ処理
- 質的変数は用いることができない
∟ 曜日を用いる場合にはget_dummiesを用いて量的データに変換
② 回帰式を求める（＋値の代入）
③ 精度確認（残差、MSE、決定係数）
＊単回帰分析との差に注目
▼練習問題
ボストンの住宅価格データ で重回帰分析を行う。
その後・・・
「標準化」と「正規化」について確認していく！
▼復習
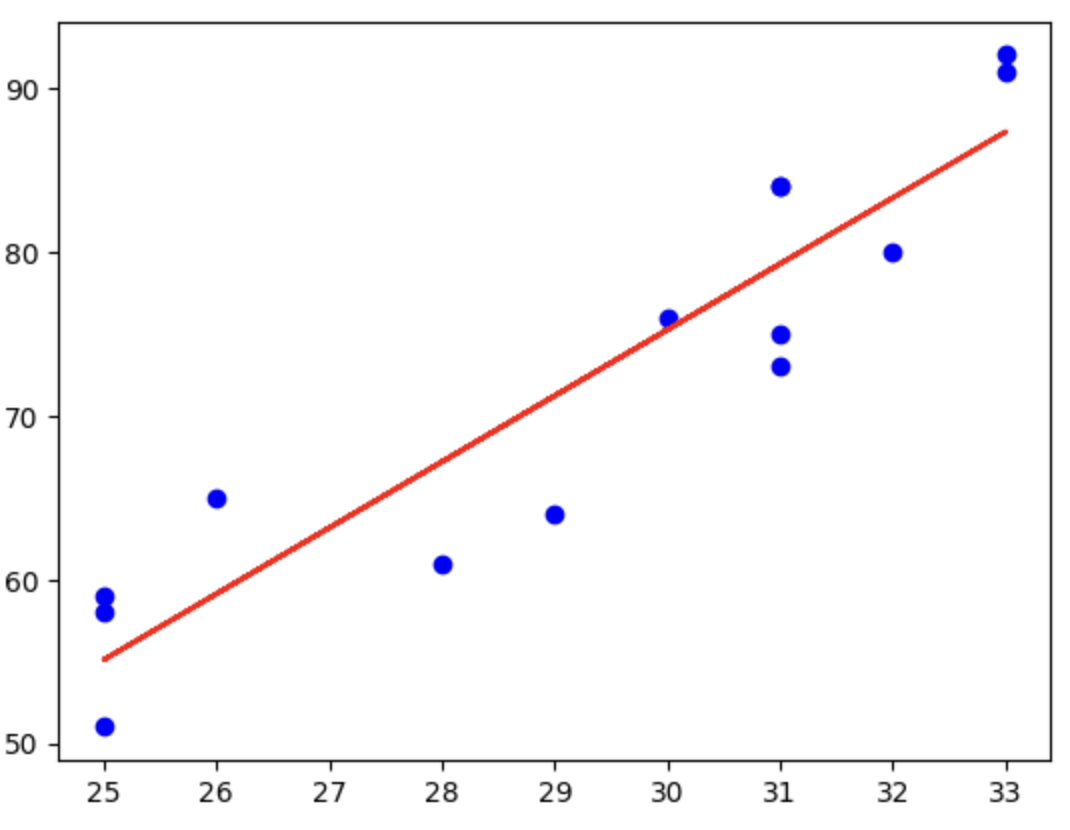
・単回帰分析の場合は、1次関数のような関係の場合に利用。
・2次以上の関数の場合は多項式回帰分析を利用する。（2次関数など）
※とはいえ、事前に多項式回帰とわかるケースは少ないらしい...。
では、yとxの関係だけに留まらないケースは？
例） y = 3a + 2b + 5c ・・・などで成り立つケース。
すなわち、説明変数が1つにならない場合。
例えば、年収（y）を決めるには、年齢（a）だけではなく、他にも役職(b)や業界(c)なども関わってくるようなイメージ。
この場合には、重回帰分析を利用する。
▼重回帰分析とは？
▪ 重回帰分析 ・・・ （説明変数が）2つ以上の入力データを使って値を予測する手法
例：身長と体脂肪率を使って体重を予測
※ 単回帰分析 ・・・ 1つの入力データを使って値を予測する手法
例：身長のデータを使って体重を予測
※参照：『重回帰分析とは？エクセルでの手順・結果の見方もわかりやすくご紹介』（https://receiptreward.jp/solution/column/multiple-regression06.html）
それでは実際に使ってみよう！！
■ 単回帰分析
- 使用するデータ
お弁当の販売数に関するデータを用いる
※データセット： https://signate.jp/competitions/24/data - 復習のため、赤字だけ確認
- 回帰式を求める意味があるか検討する
- 回帰式を求める
- 回帰式の精度を確認する ←ここだけ確認！
- 残差プロット、MSE、決定係数
【結果】
・残差プロット
・MSE、および決定係数
重回帰分析
大まかな流れ
① データの準備と可視化
・質的変数は用いることができない
・「曜日」を用いるため、get_dummiesを用いて量的データに変換
↓
② モデルの設定と訓練
↓
③ モデルの精度を確認
・残差プロット、MSE、決定係数
・単回帰分析との差に注目
① データの準備と可視化
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
# データの読み込み
train = pd.read_csv("/content/train.csv")
test = pd.read_csv("/content/test.csv")
sample = pd.read_csv("/content/sample.csv", header=None)
train.head()
2つの関係値がありそうな以下を取り上げる。
・week（曜日）、temperature（気温）の2つを説明変数として設定
・y（お弁当の売上個数）を目的変数として設定
# 'week' と 'temperature' の列を使ってダミー変数を生成
# 質的データを数値データに変換するためにget_dummiesを使用
X = pd.get_dummies(train[["week", "temperature"]])
# int型に変換することでモデルの入力として扱いやすくする
X = X.astype(int)
# ダミー変数変換後のデータを表示
print(X.head())
print()
# 目的変数を設定
y = train["y"]
曜日を、数値データに変換完了！
② モデルの設定と訓練
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X,y)
print("切片は",model.intercept_)
print("傾きは",format(pd.Series(model.coef_,index=X.columns)))
- 重回帰分析の式：
- デフォルト
- y = w₀x₀ + w₁x₁ + w₂x₂ + w₃x₃ + w₄x₄ ・・・ + b₀
- 今回の場合は、
- y = -2.5x₀ + 8.3x₁ - 9.5x₂ - 2.0x₃ + 1.8x₄ + 1.4x₅ + 135.7
- デフォルト
気温(x)が40度の月曜日に対する、売上(y)を予測してみる。
X_40 = pd.DataFrame([[40,1,0,0,0,0]],columns=["temperature","week_月","week_木","week_水","week_火","week_金"])
y_pred=model.predict(X_40)
y_pred
③ モデルの精度を確認
import matplotlib.pyplot as plt
from sklearn.metrics import mean_squared_error, r2_score
# 予測値を計算
y_pred = model.predict(X)
# 残差プロットの描画
plt.scatter(y_pred, y_pred - y, color="red")
plt.hlines(y=0, xmin=min(y_pred), xmax=max(y_pred), color="black") # 視覚化しやすいように理想値0に線を引く
plt.show()
# MSEと決定係数を計算
mse = mean_squared_error(y, y_pred)
r2 = r2_score(y, y_pred)
print("MSE:", mse)
print("決定係数:", r2)
【結果】
・残差プロット
・MSE、および決定係数
単回帰分析との差
単回帰分析のMSE、および決定係数は以下のため、精度が上がったといえる。
それでは、練習問題に行ってみよー！！
【練習問題】ボストンの住宅価格データについて
以下、3ステップを意識して実施。
■ データセットを読み込む
■ 回帰式を求める
・今回は、y（ MEDC(住宅価格の中央値) ）を目的変数とする
・それ以外をx、説明変数とする
・これらを元に、重回帰分析を行う
■ 回帰式の精度を確認
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
# データの読み込み
df = pd.read_excel("/content/boston_clean.xlsx")
# 説明変数と目的変数を分ける
X = df.drop("MEDV", axis=1) # MEDVを除外して説明変数を設定
Y = df["MEDV"] # 目的変数
# データを訓練セットとテストセットに分割
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, train_size=0.7, random_state=0)
# モデルの設定と訓練
model = LinearRegression()
model.fit(X_train, Y_train)
# モデルの切片と係数を表示
print("Intercept:", model.intercept_)
print(pd.DataFrame({"columns": X_train.columns, "Coefficient": model.coef_}).sort_values(by="Coefficient"))
# 回帰式の精度を確認するためのプロットと指標の計算
Y_train_pred = model.predict(X_train)
Y_test_pred = model.predict(X_test)
# 残差プロット
plt.scatter(Y_train_pred, Y_train_pred - Y_train, color="red", label='Train data')
plt.scatter(Y_test_pred, Y_test_pred - Y_test, color="blue", label='Test data')
plt.hlines(y=0, xmin=min(Y_train_pred), xmax=max(Y_train_pred), color="black")
plt.xlabel('Predicted Values')
plt.ylabel('Residuals')
plt.legend()
plt.show()
# MSEと決定係数の計算
mse_train = mean_squared_error(Y_train, Y_train_pred)
mse_test = mean_squared_error(Y_test, Y_test_pred)
r2_train = r2_score(Y_train, Y_train_pred)
r2_test = r2_score(Y_test, Y_test_pred)
print("MSE Train:", mse_train)
print("MSE Test:", mse_test)
print("R^2 Train:", r2_train)
print("R^2 Test:", r2_test)
▼ 傾きと切片（重回帰式）
y = -16.2x₀ - 1.5x₁ - 1.0x₂ - 0.4x₃ - 0.1x₄ ・・・ + 37.9
▼ 回帰式の精度を確認
上記をデフォルトデータとして、「標準化」「正規化」について確認する。
「標準化」「正規化」について
■ 概要
・複数の説明変数を使用する場合は、それぞれの単位や大きさが異なることが一般的であり、全てがバラバラの単位だと正確な結果が出ない。この問題を解決するために、「標準化（データを平均0、標準偏差1に変換）」、「正規化（データを0〜1の範囲に変換）」が用いられる。
※以下参考までに。
・ 標準化とは：
各データポイントから平均を引き、標準偏差で割る処理のこと。これにより、データセットの平均が0、標準偏差が1になる。
・ 正規化とは：
正規化は、データ値を最小値0、最大値1の範囲に収める変換を行うこと。これはデータの最小値と最大値に基づいて行われ、外れ値がある場合に用いやすい。
「標準化」「正規化」の実践
まずは「標準化」
ここまでは同じで、データを分割する前に 「標準化」を行う。
#標準化の準備
from sklearn.preprocessing import StandardScaler
# StandardScalerのインスタンスを作成して、変換を行う
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# 標準化されたデータをDataFrameに変換し、元のカラム名を再割り当て
X = pd.DataFrame(X_scaled, columns=X.columns)
結果（標準化）
▼ 傾きと切片（重回帰式）
▼ 回帰式の精度を確認
次に「正規化」
ここまでは同じで、データを分割する前に 「正規化」を行う。
#正規化の準備
from sklearn.preprocessing import MinMaxScaler
# MinMaxScalerのインスタンスを作成して、変換を行う
scaler = MinMaxScaler()
X_scaled = scaler.fit_transform(X)
# 正規化されたデータをDataFrameに変換し、元のカラム名を再割り当て
X = pd.DataFrame(X_scaled, columns=X.columns)
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, train_size=0.7, random_state=0)
model = LinearRegression()
model.fit(X_train, Y_train)
結果（正規化）
▼ 傾きと切片（重回帰式）
▼ 回帰式の精度を確認
・・・これらから言えること
左：デフォルト、 真ん中：標準化、 右：正規化
デフォルトの分析では、環境の悪さを示す指標「NOX」が住宅価格に最も大きな影響を与えているように見えていた。しかし、これは「NOX」の数値が比較的大きいため、他の要素と比べて影響が大きく見えただけであった。
データを均一なスケールに調整した後、実際には部屋の数「RM」が住宅価格を左右する最も重要な要素であることが分かった（真ん中、左の図より）。
低所得者の割合「LSTAT」やボストンの主要な雇用エリアからの距離「DIS」は、比較的影響が少ないことが見えてきた。
このように「標準化」や「正規化」を行うことで、実際の住宅価格に影響を与える要因をより正確に理解することができる。
以上。
続いては、 ロジスティック回帰分析へGO！！！