【多項式回帰分析】機械学習特訓 ver.2（まとめ）

【特訓 ver.2】 多項式回帰スタート！！

▼学習の流れ

まずは、大まかな流れを抑える
（ボストン市郊外の地域住宅価格に関するデータを用いる）

＊過学習についても確認していく

※過学習とは
・学習データだけに最適化され、汎用性がない状態に陥ること
・過学習した人工知能は実運用の場面では使い物にならない

（イメージ）
・テスト前に一夜漬け学習した学生のようなもの
　丸暗記状態のため、少し変更を加えられたら解けなくなる

▼練習問題
アイスコーヒの売り上げとその日の最高気温

▼復習

・単回帰分析の場合は、1次関数のような関係の場合に利用。

ただし、いつも上記のように、シンプルに比例するような関係でない場合もある。

・その場合に多項式回帰で考える。2次以上の関数に適用する（2次関数など）
　※とはいえ、事前に多項式回帰とわかるケースは少ないらしい...。

それではスタート！！

大まかな流れ

以下、3ステップで実践。

① 回帰式を求める意味があるか検討する
　 ↓
② 回帰式を求める
　 ↓
③ 回帰式の精度を確認する
＊過学習についても確認する

参照：単回帰分析（復習）

多項式回帰分析

大まかな流れ
① データの準備と可視化
　 ↓
② モデルの設定と訓練
　 ↓
③ 結果の可視化
　 ↓
④ モデルの精度を確認

① データの準備と可視化

import pandas as pd
df = pd.read_excel("/content/boston_clean.xlsx")
print(df.head())

import matplotlib.pyplot as plt
plt.scatter(df["RM"],df["MEDV"])
plt.title("RM vs MEDV")
plt.xlabel("RM")
plt.ylabel("MEDV")
plt.show()

print(df[["RM","MEDV"]].corr())

2つの関係値がありそうな以下を取り上げる。
・RM（説明変数）・・・平均部屋数（住宅の広さなど）
・MEDV（目的変数）・・・住宅の価格

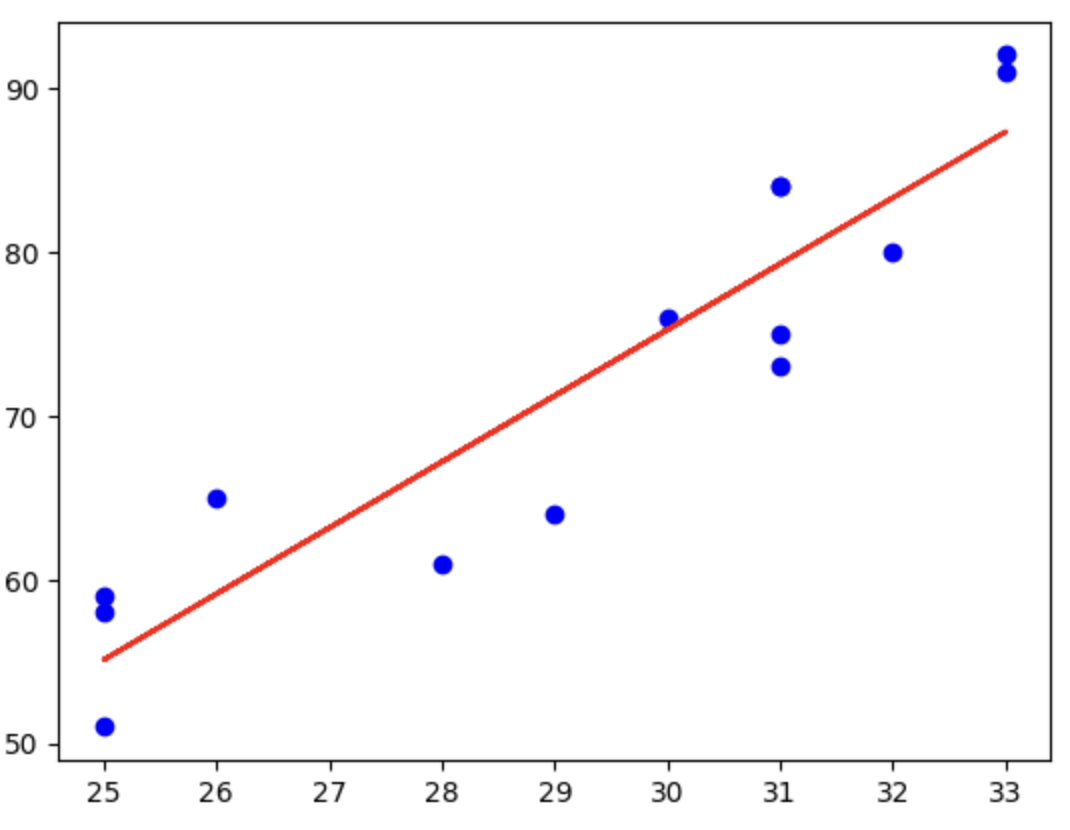
データが右肩上がりになっているため、回帰直線を引く意味があると考える。
また、相関係数が0.7と緩やかな正の相関があると言える。

② モデルの設定と訓練

まずは学習データと検証データの分割。そして可視化。

X = df["RM"].values.reshape(-1,1) # 部屋の数をNumpy配列にして、それを表のような形に変えます
Y = df["MEDV"].values  # 家の価格もNumpy配列にする

from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, train_size=0.7, random_state=0)

import matplotlib.pyplot as plt
plt.scatter(X_train,Y_train,color="blue",label="train")
plt.scatter(X_test,Y_test,color="black",label="test")

plt.title("RM vs MEDV")
plt.legend()
plt.show()

from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
import numpy as np

# 多項式特徴量の生成
poly = PolynomialFeatures(degree=4)
X_poly_train = poly.fit_transform(X_train)

# モデルの訓練
model = LinearRegression()
model.fit(X_poly_train, Y_train)

単回帰との違いについて（1次関数）。
こちらはX、Yとの関係が非常にシンプルになっているためそのままmodelに突っ込めばよかった。

一方でそれ以上の関数（2次以上の関数）の場合は、複雑になるため、まずは、Xの累乗値の値を別で求めてあげる必要になる。
※y = ax²の x²の部分

手順としては、
・X、 Yの設定をする
・modelに当てはめる　が単回帰の方法だが、その間にワンクッションを挟む。

具体的には
・X、 Yの設定をする
　　　　 ↓
・高次数にも対応するように「PolynomialFeatures」を設定する
　　　　 ↓
・高次数に対応したX（今回でいうとX_poly）を用いてmodelを訓練する

【コードの説明】
・poly = PolynomialFeatures(degree=4)
　これはdegree=4で4次関数を表す。
　変数Xを4次関数に対応させるための前準備。
・X_poly = poly.fit_transform(X)
　Xの0乗、1乗、2乗、3乗、4乗と順番に出力する。
　※degree=4のため、4乗まで。

出力結果参照： array([[1.00000000e+00, 5.01900000e+00, 2.51903610e+01, 1.26430422e+02, 6.34554287e+02],・・・・]])

③ 結果の可視化

#可視化する
plt.scatter(X_train,Y_train,color="blue")
plt.scatter(X_test,Y_test,color="black")

# 図形を滑らかにするため、かつ、X_plotを並び替える必要がある
X_plot = np.linspace(min(X_train), max(X_train), 100).reshape(-1,1)
X_poly_plot = poly.transform(X_plot)

# 予測結果のプロット
plt.plot(X_plot, model.predict(X_poly_plot), color="red")
plt.show()

Xは、基本的に順番が並んでいるわけではないため、plt.plotで表示をすると、線がグシャグシャになる。そのため、linspaceを用いて昇順に並び替える必要がある。

④ モデルの精度を確認

#MSE
from sklearn.metrics import mean_squared_error

#決定係数
from sklearn.metrics import r2_score

# X_train と X_test を多項式特徴量に変換
X_poly_train = poly.transform(X_train)
X_poly_test = poly.transform(X_test)

print(f"mse(train)は、{mean_squared_error(Y_train, model.predict(X_poly_train))}")
print(f"mse(test)は、{mean_squared_error(Y_test, model.predict(X_poly_test))}")
print()
print(f"r^2(train)は、{r2_score(Y_train, model.predict(X_poly_train))}")
print(f"r^2(test)は、{r2_score(Y_test, model.predict(X_poly_test))}")

完成。
モデルの精度を追求するため、degree（次数の値）を変更して比較してみる。
【グラフを作成して可視化】　→ 【決定係数・MSEで精度を比較】の順で行う。

【グラフを作成して可視化】

まずは、グラフを作成して可視化。
一括で比較するためにPipelineを用いて作成をする。

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import train_test_split

# データの読み込み
df = pd.read_excel("/content/boston_clean.xlsx")

# 変数の定義
X = df["RM"].values.reshape(-1,1)  # 部屋数
Y = df["MEDV"].values  # 住宅価格

# データの分割
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, train_size=0.7, random_state=0)

# 訓練データとテストデータの可視化
plt.scatter(X_train, Y_train, color="blue", label="Train")
plt.scatter(X_test, Y_test, color="black", label="Test")
plt.title("RM vs MEDV")
plt.legend()
plt.show()

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression

#次数=1（線形回帰）
model_1 = Pipeline([
    ("poly",PolynomialFeatures(degree=1)),
    ("linear",LinearRegression())
])
model_1.fit(X_train,Y_train)

#次数=3
model_3 = Pipeline([
    ("poly",PolynomialFeatures(degree=3)),
    ("linear",LinearRegression())
])
model_3.fit(X_train,Y_train)

#次数=6
model_6 = Pipeline([
    ("poly",PolynomialFeatures(degree=6)),
    ("linear",LinearRegression())
])
model_6.fit(X_train,Y_train)

#次数=8
model_8 = Pipeline([
    ("poly",PolynomialFeatures(degree=8)),
    ("linear",LinearRegression())
])
model_8.fit(X_train,Y_train)

#可視化する
plt.scatter(X_train,Y_train,color="blue")
plt.scatter(X_test,Y_test,color="black")

X_plot = np.linspace(min(X_train), max(X_train), 100).reshape(-1,1)

plt.plot(X_plot,model_1.predict(X_plot),color="red",label="degree=1")
plt.plot(X_plot,model_3.predict(X_plot),color="green",label="degree=3")
plt.plot(X_plot,model_6.predict(X_plot),color="yellow",label="degree=6")
plt.plot(X_plot,model_8.predict(X_plot),color="purple",label="degree=8")

plt.legend()
plt.show()

【決定係数・MSEで精度を比較】

次に、決定係数・MSEで精度を比較化。

from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score

#MSE
print(f"mse1(train)は、{mean_squared_error(Y_train, model_1.predict(X_train))}")
print(f"mse1(test)は、{mean_squared_error(Y_test, model_1.predict(X_test))}")
print()
print(f"mse3(train)は、{mean_squared_error(Y_train, model_3.predict(X_train))}")
print(f"mse3(test)は、{mean_squared_error(Y_test, model_3.predict(X_test))}")
print()
print(f"mse6(train)は、{mean_squared_error(Y_train, model_6.predict(X_train))}")
print(f"mse6(test)は、{mean_squared_error(Y_test, model_6.predict(X_test))}")
print()
print(f"mse8(train)は、{mean_squared_error(Y_train, model_8.predict(X_train))}")
print(f"mse8(test)は、{mean_squared_error(Y_test, model_8.predict(X_test))}")

print()

#決定係数
print(f"r^2 1(train)は、{r2_score(Y_train, model_1.predict(X_train))}")
print(f"r^2 1(test)は、{r2_score(Y_test, model_1.predict(X_test))}")
print()
print(f"r^2 3(train)は、{r2_score(Y_train, model_3.predict(X_train))}")
print(f"r^2 3(test)は、{r2_score(Y_test, model_3.predict(X_test))}")
print()
print(f"r^2 6(train)は、{r2_score(Y_train, model_6.predict(X_train))}")
print(f"r^2 6(test)は、{r2_score(Y_test, model_6.predict(X_test))}")
print()
print(f"r^2 8(train)は、{r2_score(Y_train, model_8.predict(X_train))}")
print(f"r^2 8(test)は、{r2_score(Y_test, model_8.predict(X_test))}")
print()

上記の結果を元に過学習について確認する。

過学習について

■過学習とは
・学習データだけに最適化され、汎用性がない状態に陥ること
・過学習した人工知能は実運用の場面では使い物にならない

（イメージ）
・テスト前に一夜漬け学習した学生のようなもの
　丸暗記状態のため、少し変更を加えられたら解けなくなる

■先ほどの結果を元に・・・
決定係数（1に近づくほど精度が高い）で考えてみる。
trainデータは練習用、すなわち過去問と全く同じというイメージ。
testデータは本番用、こちらの精度も高くないと、丸暗記パターンという感じ。

r^2 1(train)は、0.5026497630040827
r^2 1(test)は、0.43514364832115193

r^2 3(train)は、0.5832580086428305
r^2 3(test)は、0.5049156410773745　← 精度高い

r^2 6(train)は、0.6235383874932028
r^2 6(test)は、0.504694432378775

r^2 8(train)は、0.6256466167534778　← 精度高い
r^2 8(test)は、0.4845183456329236

訓練用で一番精度が高かったのは、drgree=8が一番精度が高いが、テストデータの場合は、degree=3が一番精度が高い。
すなわち、練習に強いのは今回だとdegree=8に軍配が上がるが、本番で勝ち進めるのはdegree=3。

これらより、訓練用にフィットすることだけを考えていてもテスト用で精度が落ちてしまうケースがあることがわかる。
これを「過学習」という。

【練習問題】 喫茶店のアイスコーヒーの売り上げとその日の最高気温についてのデータ

以下、4ステップを意識して実施。
・データの準備と可視化
・モデルの設定と訓練（多項式回帰を用いる）
・結果の可視化
・モデルの精度を確認

import pandas as pd
train_df = pd.read_csv("/content/icecoffee_train.csv")
test_df = pd.read_csv("/content/icecoffee_test.csv")

X_train = train_df["temperature"].values.reshape(-1,1)
Y_train = train_df["icecoffee"].values 

X_test = test_df["temperature"].values.reshape(-1,1)
Y_test = test_df["icecoffee"].values 

import matplotlib.pyplot as plt
plt.scatter(X_train,Y_train,color="blue",label="train")
plt.scatter(X_test,Y_test,color="black",label="test")

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
import numpy as np

#次数=1（線形回帰）
model_1 = Pipeline([
    ("poly",PolynomialFeatures(degree=1)),
    ("linear",LinearRegression())
])
model_1.fit(X_train,Y_train)

#次数=2
model_2 = Pipeline([
    ("poly",PolynomialFeatures(degree=2)),
    ("linear",LinearRegression())
])
model_2.fit(X_train,Y_train)

#次数=3
model_3 = Pipeline([
    ("poly",PolynomialFeatures(degree=3)),
    ("linear",LinearRegression())
])
model_3.fit(X_train,Y_train)

#次数=4
model_4 = Pipeline([
    ("poly",PolynomialFeatures(degree=4)),
    ("linear",LinearRegression())
])
model_4.fit(X_train,Y_train)

#可視化する
plt.scatter(X_train,Y_train,color="blue")
plt.scatter(X_test,Y_test,color="black")

X_plot = np.linspace(min(X_train), max(X_train), 100).reshape(-1,1)

plt.plot(X_plot,model_1.predict(X_plot),color="red",label="degree=1")
plt.plot(X_plot,model_2.predict(X_plot),color="green",label="degree=2")
plt.plot(X_plot,model_3.predict(X_plot),color="yellow",label="degree=3")
plt.plot(X_plot,model_4.predict(X_plot),color="purple",label="degree=4")

plt.legend()
plt.show()

評価の精度を確認。

from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score

#MSE
print(f"mse1(train)は、{mean_squared_error(Y_train, model_1.predict(X_train))}")
print(f"mse1(test)は、{mean_squared_error(Y_test, model_1.predict(X_test))}")
print()
print(f"mse2(train)は、{mean_squared_error(Y_train, model_2.predict(X_train))}")
print(f"mse2(test)は、{mean_squared_error(Y_test, model_2.predict(X_test))}")
print()
print(f"mse3(train)は、{mean_squared_error(Y_train, model_3.predict(X_train))}")
print(f"mse3(test)は、{mean_squared_error(Y_test, model_3.predict(X_test))}")
print()
print(f"mse4(train)は、{mean_squared_error(Y_train, model_4.predict(X_train))}")
print(f"mse4(test)は、{mean_squared_error(Y_test, model_4.predict(X_test))}")

print()

#決定係数
print(f"r^2 1(train)は、{r2_score(Y_train, model_1.predict(X_train))}")
print(f"r^2 1(test)は、{r2_score(Y_test, model_1.predict(X_test))}")
print()
print(f"r^2 2(train)は、{r2_score(Y_train, model_2.predict(X_train))}")
print(f"r^2 2(test)は、{r2_score(Y_test, model_2.predict(X_test))}")
print()
print(f"r^2 3(train)は、{r2_score(Y_train, model_3.predict(X_train))}")
print(f"r^2 3(test)は、{r2_score(Y_test, model_3.predict(X_test))}")
print()
print(f"r^2 4(train)は、{r2_score(Y_train, model_4.predict(X_train))}")
print(f"r^2 4(test)は、{r2_score(Y_test, model_4.predict(X_test))}")
print()

決定係数は、全て低すぎる・・・。
testデータ引っ張ってくるもの間違えたか？？！！と思うくらい。

強いていえば、degree=4が一番精度がマシだった。

r^2 1(train)は、0.8556544726255537
r^2 1(test)は、-5.3449939075596165

r^2 2(train)は、0.8884891089426318
r^2 2(test)は、-7.748643986333793

r^2 3(train)は、0.8886629164651121
r^2 3(test)は、-8.252067318696229

r^2 4(train)は、0.8970122480831968　← 精度高い
r^2 4(test)は、-2.9921813252509404　← 精度高い（まだマシ）

続いては、 重回帰分析へGO！！！