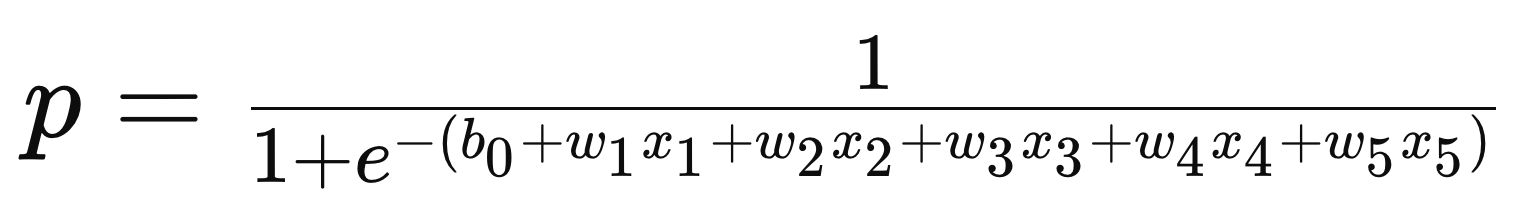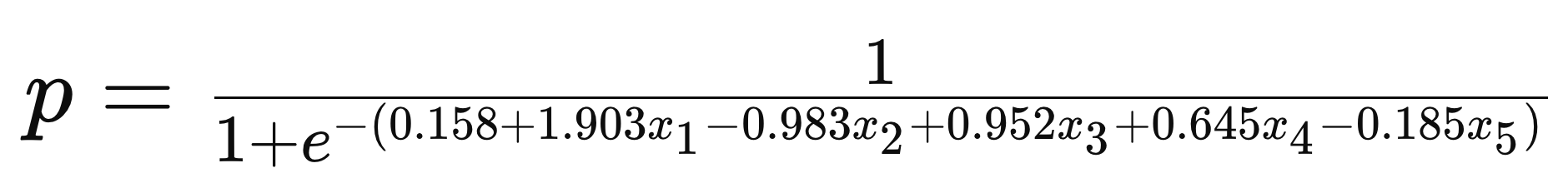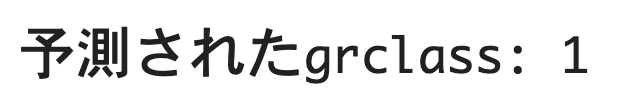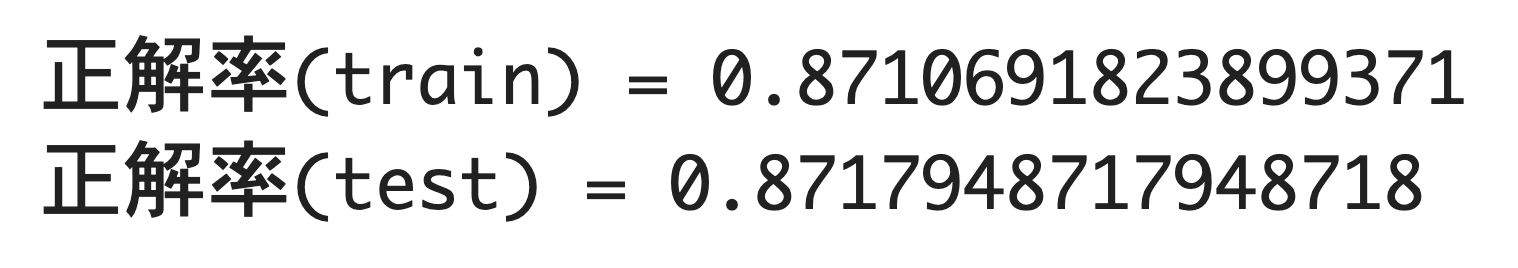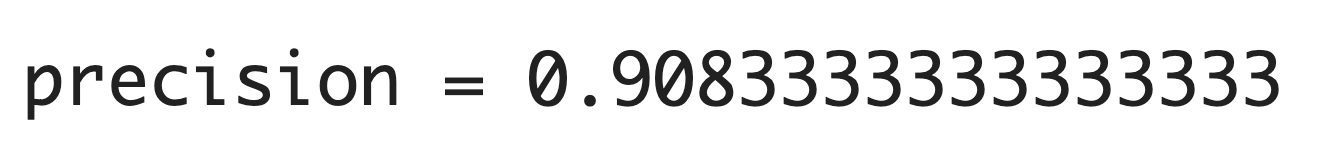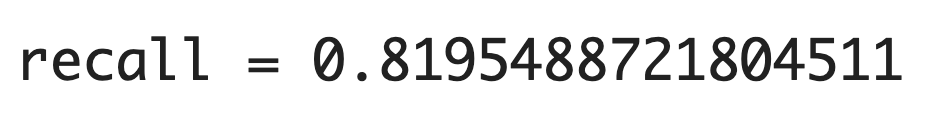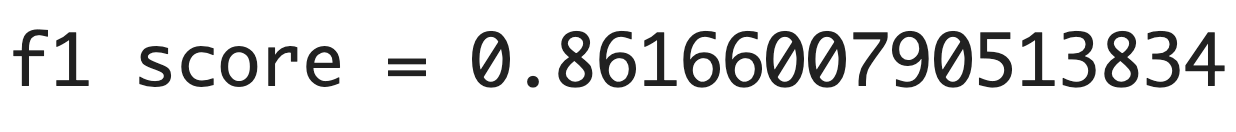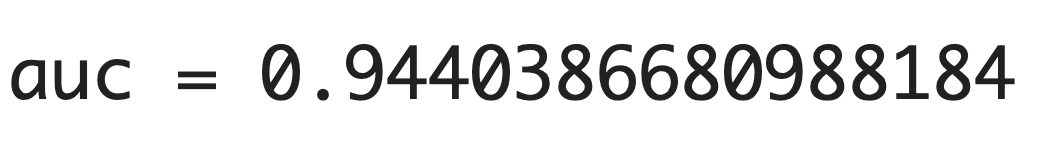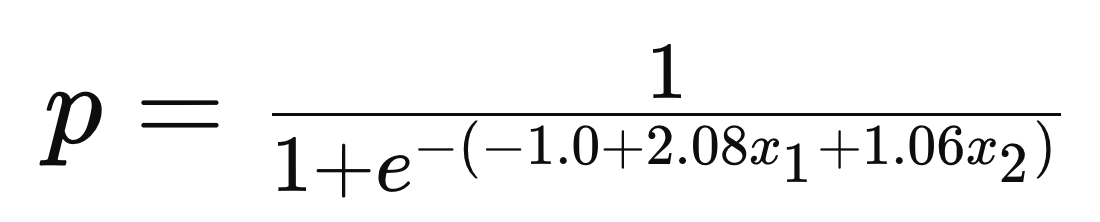【特訓 ver.4】 ロジスティック回帰スタート!!
※この記事ではロジスティック回帰分析についてまとめます
▼学習の流れ
まずはロジスティック回帰分析の基本を押さえ、具体的な問題を通して理解を深める。
■使用するデータ
握力測定に関するデータ
(実際の握力測定なしに、身長の値を用いて学生の握力分類を行う)
※データセット:後日
■ ロジスティック回帰分析について学習する
大まかな流れ)
① データ読み込みや前処理、分割
- 質的変数は用いることができない
② モデルの設定と訓練
- 「ロジスティック回帰分析」で実施する
③ モデルの精度の確認
- 精度について、以下6項目で確認していく
分類における「学習モデルの性能評価」について確認していく!
(1) 混同行列(confusion matrix)
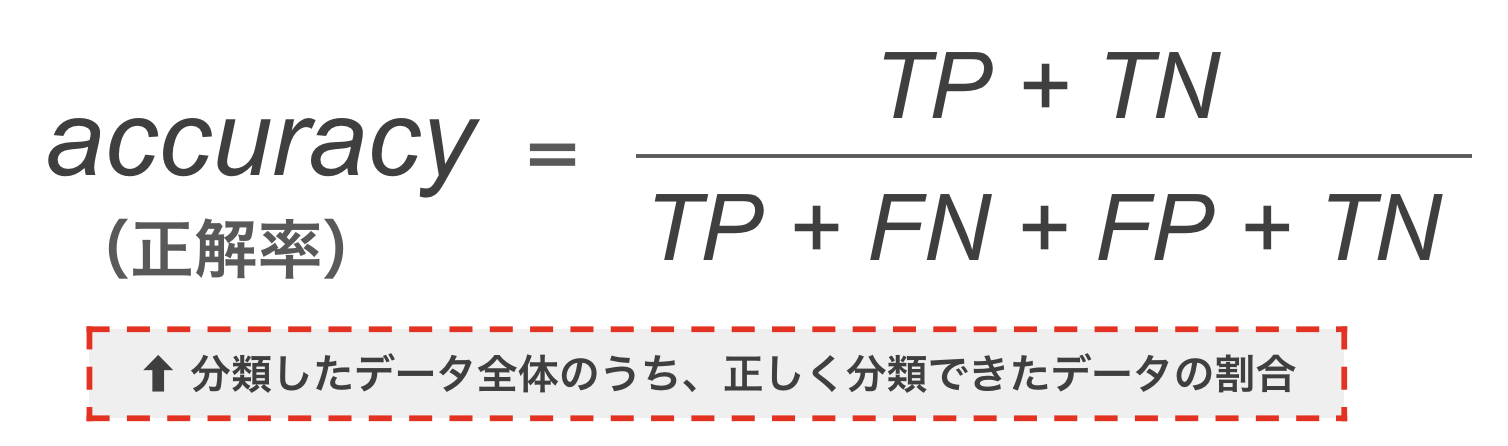
(2) 正解率(accuracy)
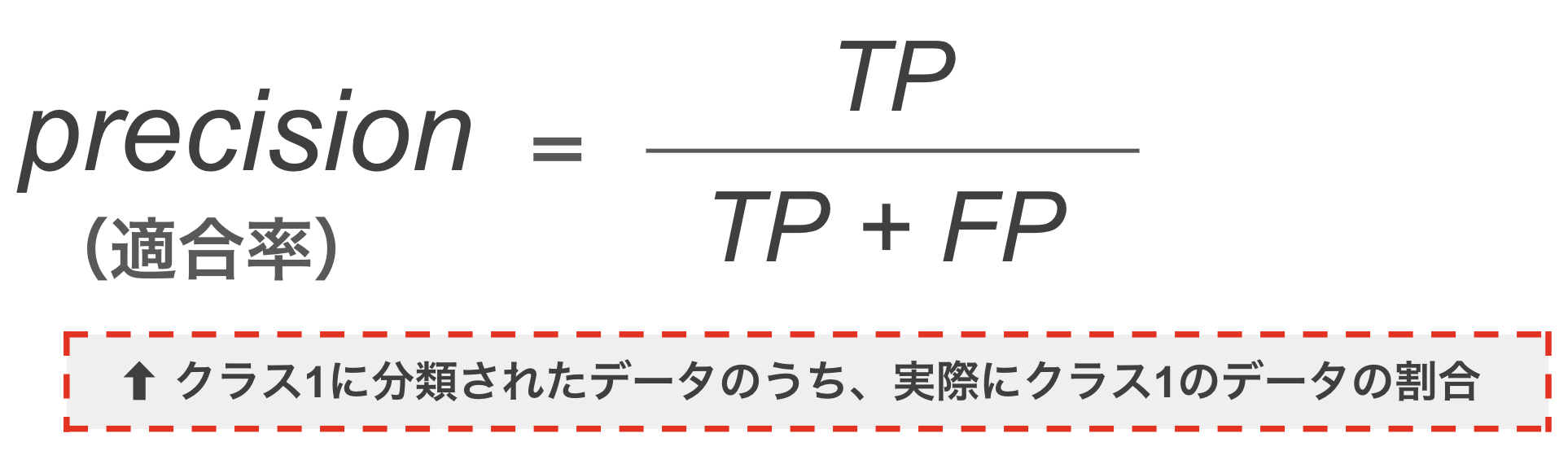
(3) 適合率(precision)
(4) 再現率(recall)
(5) F1スコア(F1-score)
(6) AUC(曲線下面積)
▼練習問題
年齢、年収によってある商品を購入したかどうか でロジスティック回帰分析を行う。
▼復習
・単回帰分析の場合は、1次関数のような関係の場合に利用。すなわち、xに応じてyも比例するような際に利用をする。
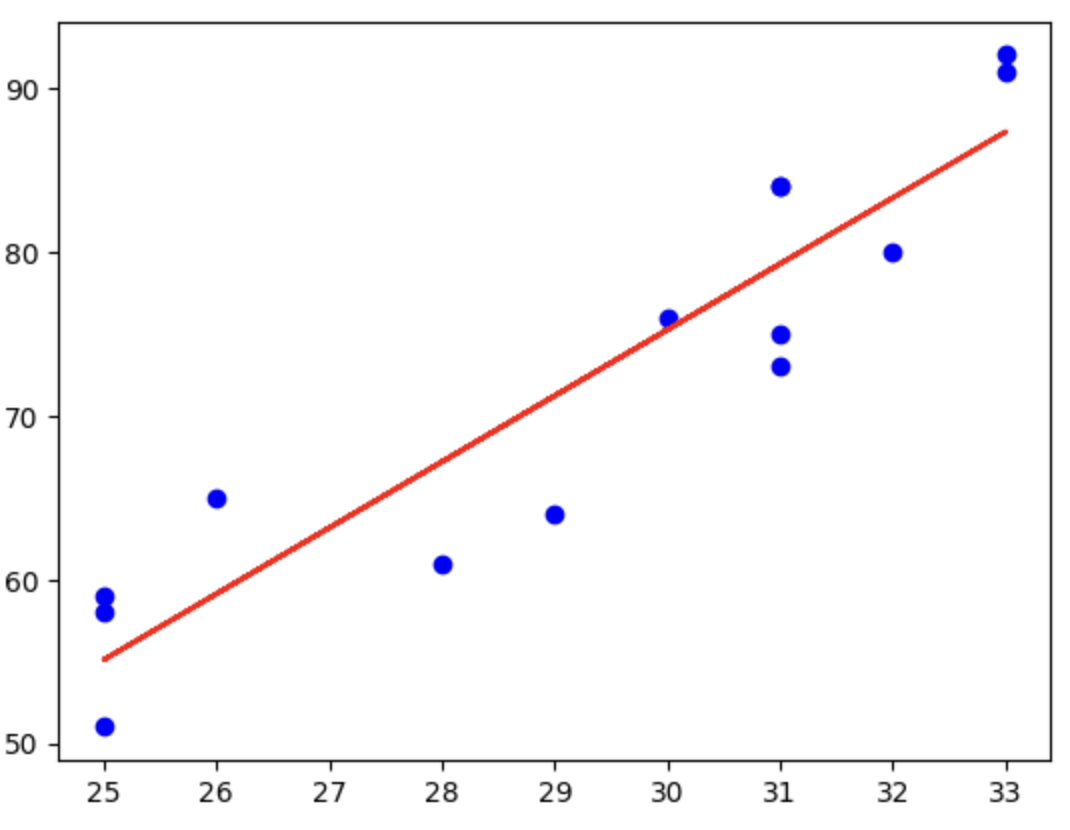
・今まで学習してきた回帰分析は、
▪ 単回帰分析 ・・・ 1つの入力データを使って値を予測する手法
例:身長のデータを使って体重を予測
▪ 重回帰分析 ・・・ 2つ以上の入力データを使って値を予測する手法
例:身長と体脂肪率を使って体重を予測
すなわち、入れる値に応じて、結果が定量的に出てくるものを求めるときに有効であった。
では、結果が2択になるケースではどうするか。 例) ◯か×か、合格か不合格か、など
以下、テストの点数(横軸)に応じて、合否(縦軸)を算出するようなものを出している。合格は1、不合格は0として表示。
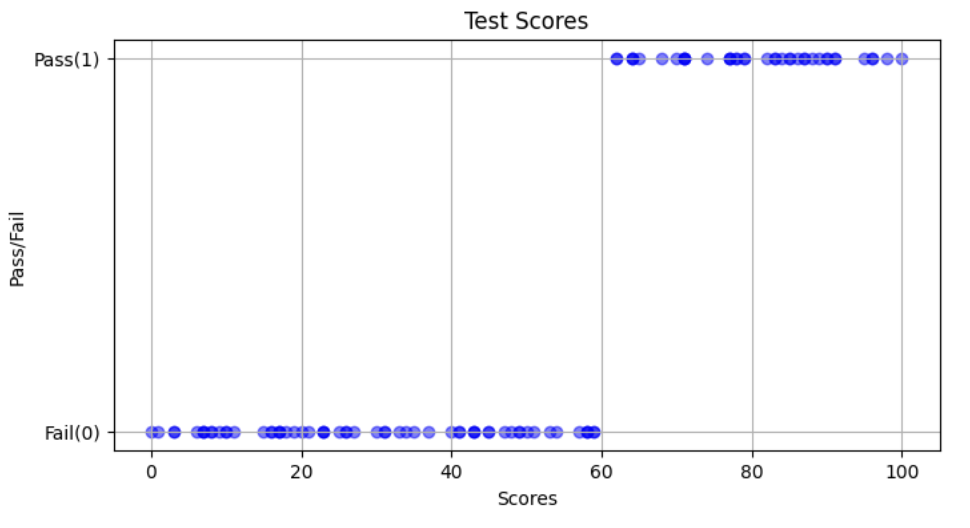
こちらのプロットした値に対して、回帰分析をすると赤線のグラフが得られると考えられる。
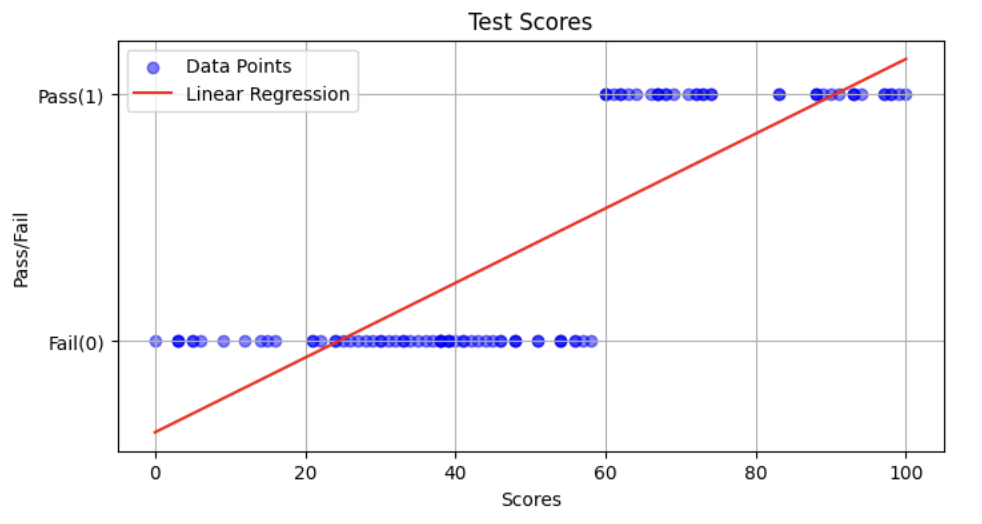
違和感しかない・・・。
この赤色の直線を元に、テストの点数が「50点」「70点」で結果を出力した場合には、それぞれ「0.35」「0.63」と出力された。本来は、1 or 0(合格or不合格)で表示して欲しいのに、このような微妙な数字で出されても判断ができない。
こういった場合には、ロジスティック回帰分析を利用する。
▼ロジスティック回帰分析とは?
いくつかの要因(説明変数)から「2値の結果(目的変数)」が起こる確率を説明・予測することができる統計手法のこと。
単回帰、重回帰との違いも踏まえながらまとめると以下のようになる。
目的変数が2択(質的変数)になるものは、基本的にロジスティック回帰分析を用いるという認識でよさそう。
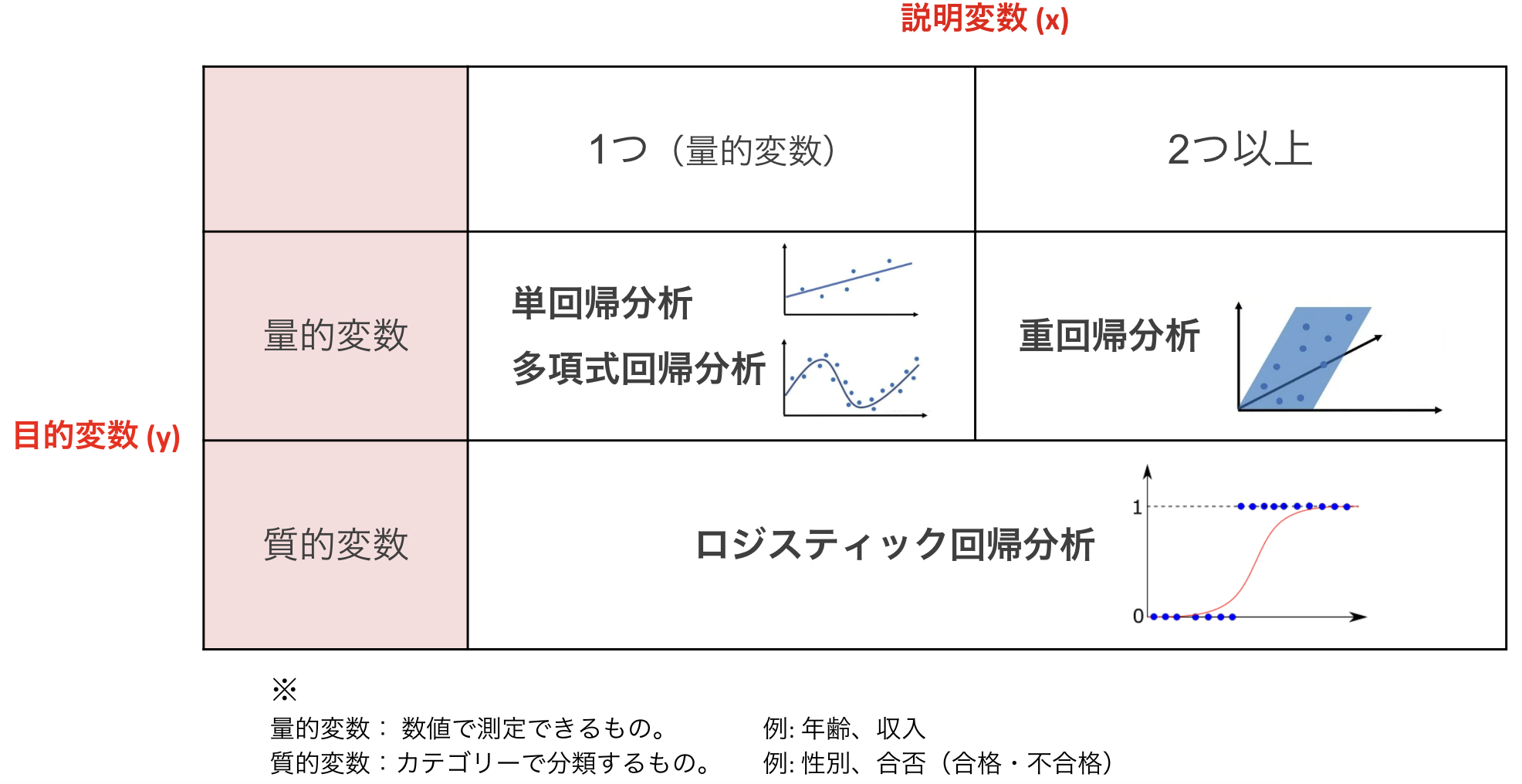
もう少し具体的に。
目的変数が質的なのか量的なのかで使い分ける。
ロジスティック回帰分析では確率( 0 or 1 )を求めたいので、重回帰などは適さない。
それでは実際に使ってみよう!!
【ロジスティック回帰分析】
大まかな流れ
① データ読み込みや前処理、分割
- 質的変数は用いることができない
② モデルの設定と訓練
- 「ロジスティック回帰分析」で実施する
③ モデルの精度の確認
- 精度について、以下6項目で確認していく
(1) 混同行列(confusion matrix)
(2) 正解率(accuracy)
(3) 適合率(precision)
(4) 再現率(recall)
(5) F1スコア(F1-score)
(6) AUC(曲線下面積)
① データ読み込みや前処理、分割
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# データの読み込み
df = pd.read_csv("/content/akuryoku.csv")
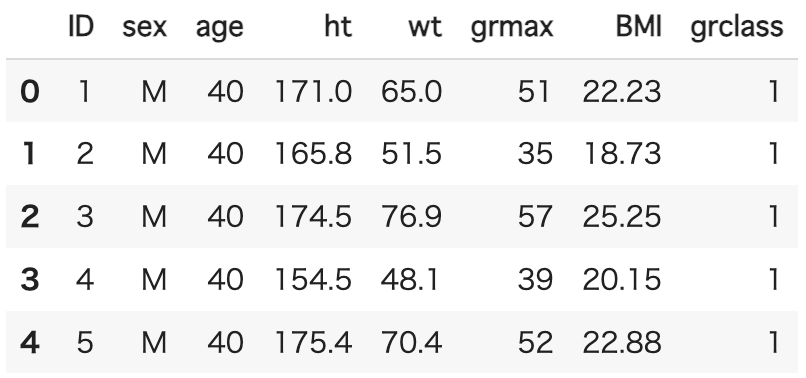
df.head()
〔説明変数〕
・sex(性別)、age(年齢)、ht(身長)、wt(体重)、BMIの5つを用いる
・sexは0、1に変更する
〔目的変数〕
・grclass・・・1=握力強い、0=握力弱い
#質的変数を量的変数に変換
df['sex'] = df['sex'].replace({'M': 1, 'F': 0})
#説明変数と目的変数に分ける
x = df[["sex","age","ht","wt","BMI"]].values
y = df["grclass"].values
#データを学習用と検証用に分割
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test = train_test_split(
x,y,train_size=0.7,random_state=0)
#標準化
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
x_train_std = sc.fit_transform(x_train)
x_test_std = sc.transform(x_test)
② モデルの設定と訓練
from sklearn.linear_model import LogisticRegression
model = LogisticRegression()
model.fit(x_train_std,y_train)
print(f"切片は {model.intercept_}")
print(f"傾きは {model.coef_}")
以下の条件を持つ(x)に対する、握力分類(y)を予測してみる。
性別:男性(1)
年齢:30歳
身長:175 cm
体重:70 kg
BMI:22.9
# 予測用データを作成して標準化
x_new = pd.DataFrame([[1, 30, 175, 70, 22.9]], columns=["sex", "age", "ht", "wt", "BMI"])
x_new_std = sc.transform(x_new)
# 予測実行
y_pred = model.predict(x_new_std)
print("予測されたgrclass:", y_pred[0])
③ モデルの精度を確認
(1) 混同行列(confusion matrix)
from sklearn.metrics import confusion_matrix
print("confusion_matrix =")
print(confusion_matrix(y_true=y_test,y_pred=model.predict(x_test_std)))
※y_true = y_test
※y_pred = model.predict(x_test_std))
↑ 正解データ = y_test 、
予測データ = model.predict( )で定義付け
青丸が正しく判定できた数になる。
総合的に「偽」が少ない方が、精度は高い。
(2) 正解率(accuracy)
print("正解率(train) =", model.score(x_train_std, y_train))
print("正解率(test) =", model.score(x_test_std, y_test))
(3) 適合率(precision)
from sklearn.metrics import precision_score
print("precision =",precision_score(y_true=y_test,y_pred=model.predict(x_test_std)))
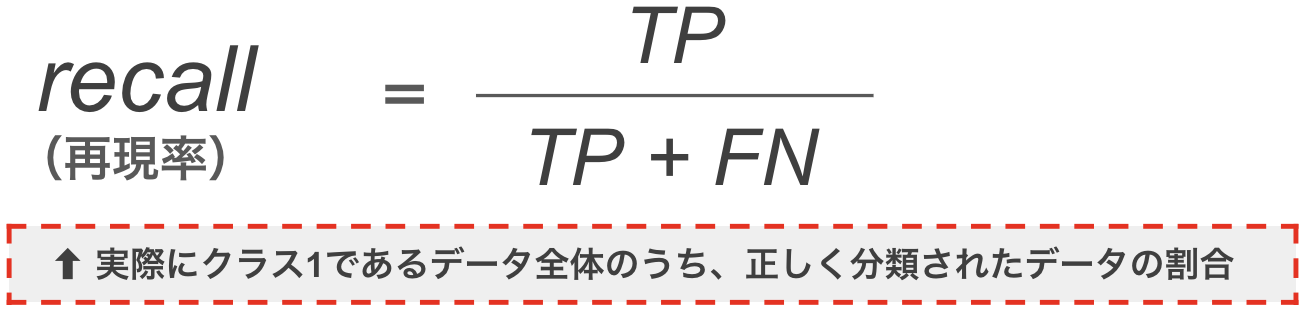
(4) 再現率(recall)
from sklearn.metrics import recall_score
print("recall =",recall_score(y_true=y_test,y_pred=model.predict(x_test_std)))
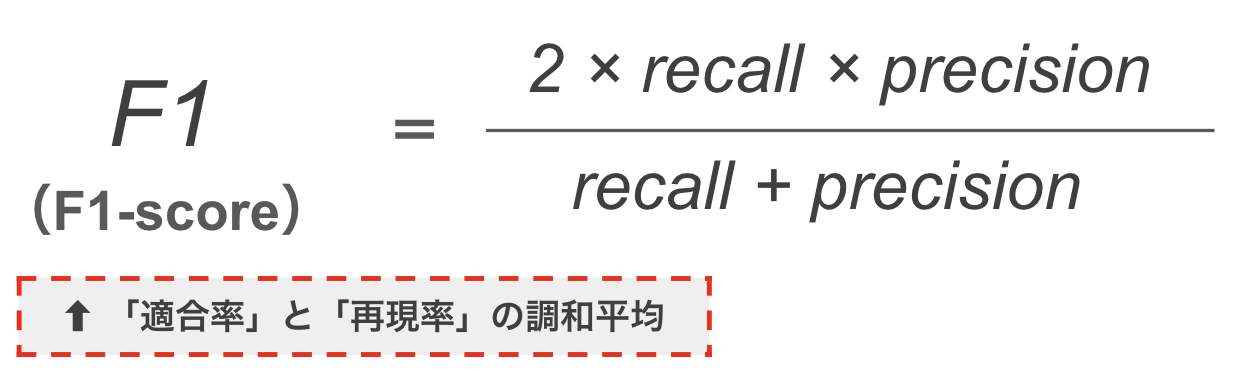
(5) F1スコア(F1-score)
from sklearn.metrics import f1_score
print("f1 score =",f1_score(y_true=y_test,y_pred=model.predict(x_test_std)))
ここまでの内容を簡単にまとめると・・・
| 項目 | 説明 | 値 |
|---|---|---|
| (1)混同行列(confusion matrix) | 予測の正誤を表す表。 | [[129, 11], [24, 109]] |
| (2)-1 正解率(train) | 訓練データにおける正解率。 | 0.8711 |
| (2)-2 正解率(test) | テストデータにおける正解率。 | 0.8718 |
| (3) 適合率(precision) | 正と予測したものの正確さ。 | 0.9083 |
| (4) 再現率(recall) | 実際の正をどれだけ捉えたか。 | 0.8195 |
| (5) F1スコア(F1-score) | 適合率と再現率の調和平均。 | 0.8617 |
(6) AUC(曲線下面積)
AUCスコア(Area Under the Curve)は、ROC曲線(Receiver Operating Characteristic Curve)の下の面積を指す。このスコアは0から1までの値を取り、1に近いほどモデルの性能が良いことを示す。
from sklearn.metrics import roc_auc_score
print("auc =",roc_auc_score(y_true=y_test,
y_score=model.predict_proba(x_test_std)[:,1]))
※y_true = y_test
※y_score = model.predict_proba(x_test_std)[:,1]
↑ 正解データ = y_test 、
スコアデータ = model.predict_proba(x_test_std)[:,1]で定義付け
何をしている?
テストデータから各データが特定のクラス(握力が強いか)に属する確率を計算。
どうやっているのか?
model.predict_proba(x_test_std) はテストデータの各サンプルのクラス確率を計算。 [:,1]は「1」クラス(握力が強い)の確率を抽出。これにより、サンプルが「握力が強い」とされる確信度を示す。
簡単な例で考えてみる
例えば、テストデータに10人の実験者がいる。モデルは各人の「握力が強い」確率を計算し、model.predict_proba(x_test_std)[:,1] でそれをリスト化。数値0.8が出れば、その人の握力が強い確率は80%と予測される。
94%と高い精度が出ている。つまり、このモデルが「この人の握力は強い」と判断した場合、その予測は信頼できると言える。
※参照:ROC曲線も可視化してみる
from sklearn.metrics import roc_curve, auc
# モデルが予測した「握力が強い」確率を取得
y_score = model.predict_proba(x_test_std)[:, 1]
# ROC曲線のデータを計算(実際のラベルと予測確率を使って)
fpr, tpr, thresholds = roc_curve(y_true=y_test, y_score=y_score)
# ROC曲線をプロット
plt.plot(fpr, tpr, label="ROC curve (area = %0.2f)" % auc(fpr, tpr))
# ランダムな予測の場合の線をプロット(対角線)
plt.plot([0, 1], [0, 1], linestyle="--", label="Random")
# 理想的な予測の場合の線をプロット(階段形)
plt.plot([0, 0, 1], [0, 1, 1], linestyle="--", label="Ideal")
plt.legend()
plt.show()
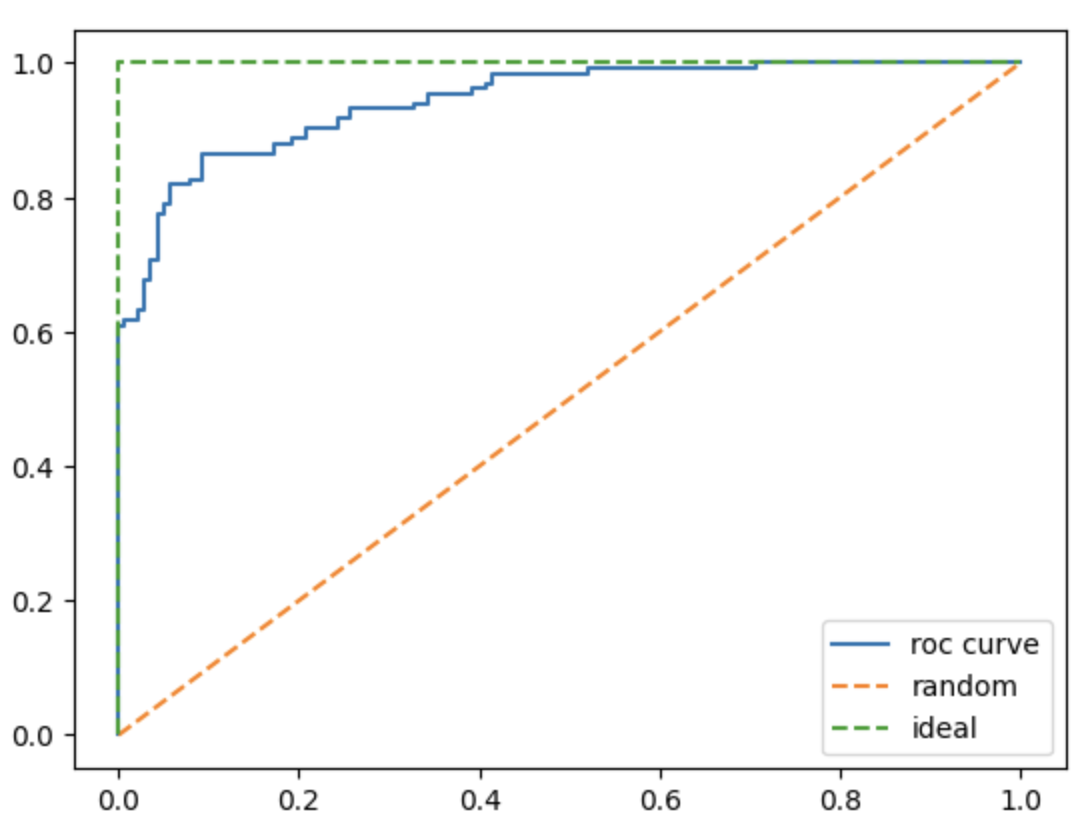
青 :ROC曲線(これの下の面積がAUC)、面積が大きいほど正確
緑 :理想値 黄色:適当な値
※緑、黄色の線は、指標として書いておくことが多い。
※横軸:偽陽性率(FP率)、縦軸:真陽性率(TP率)
それでは、練習問題に行ってみよー!!
【練習問題】年齢、年収によってある商品を購入したかどうか
以下、3ステップを意識して実施。
① データ読み込みや前処理、分割
- 質的変数は用いることができない
② モデルの設定と訓練
- 「ロジスティック回帰分析」で実施する
③ モデルの精度の確認
- 精度について、以下6項目で確認していく
(1) 混同行列(confusion matrix)
(2) 正解率(accuracy)
(3) 適合率(precision)
(4) 再現率(recall)
(5) F1スコア(F1-score)
(6) AUC(曲線下面積)
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import confusion_matrix, precision_score, recall_score, f1_score, roc_auc_score
# データの読み込み
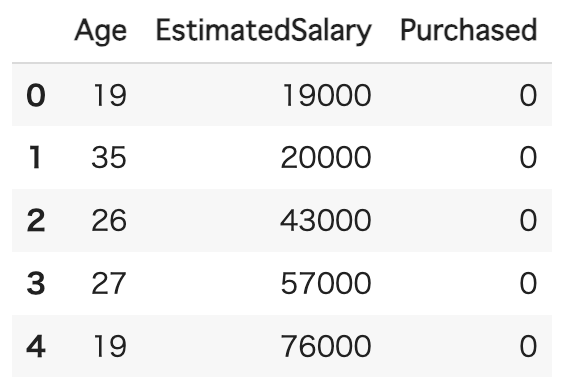
df = pd.read_csv("/content/Social_Network_Ads.csv")
print(df.head())
# 必要なデータの抽出
x = df[["Age", "EstimatedSalary"]].values
y = df["Purchased"].values
# データを学習用と検証用に分割
x_train, x_test, y_train, y_test = train_test_split(x, y, train_size=0.7, random_state=0)
# データの標準化
sc = StandardScaler()
x_train_std = sc.fit_transform(x_train)
x_test_std = sc.transform(x_test)
# ロジスティック回帰モデルの訓練
model = LogisticRegression()
model.fit(x_train_std, y_train)
# モデルのパラメータ表示
print(f"切片は {model.intercept_}")
print(f"傾きは {model.coef_}")
# 混同行列の出力
print("Confusion Matrix:")
print(confusion_matrix(y_true=y_test, y_pred=model.predict(x_test_std)))
# 性能指標の計算と表示
print("正解率(train) =", model.score(x_train_std, y_train))
print("正解率(test) =", model.score(x_test_std, y_test))
print("適合率 =", precision_score(y_true=y_test, y_pred=model.predict(x_test_std)))
print("再現率 =", recall_score(y_true=y_test, y_pred=model.predict(x_test_std)))
print("F1スコア =", f1_score(y_true=y_test, y_pred=model.predict(x_test_std)))
print("AUC =", roc_auc_score(y_true=y_test, y_score=model.predict_proba(x_test_std)[:, 1]))
▼ 傾きと切片(ロジスティック回帰式)
切片は [-0.998508]
傾きは [[2.08013198 1.06134466]]
▼ 回帰式の精度を確認
(1) 混同行列(confusion matrix)
(2) 正解率(accuracy)
(3) 適合率(precision)
(4) 再現率(recall)
(5) F1スコア(F1-score)
(6) AUC(曲線下面積)

テストデータにおける正解率は約87%で、AUCスコアは約0.95と非常に高い性能を示した。モデルの適合率も高い一方で、再現率は約73%と伸び代がある。実際の現場で活用する際には、追加のデータ収集、特徴量エンジニアリング、異なるアルゴリズムの試行、ハイパーパラメータの最適化などで精度を上げていく必要がありそう。
以上。
続いては、 SVM分析へGO!!!