【特訓 ver.5】 SVMスタート！！
※この記事では、SVM（サポートベクターマシン）を用いた分類手法についてまとめます
▼学習の流れ
まずはSVM（分類）の基本を押さえ、具体的な分析例を通して理解を深める。
※なお、SVMは回帰問題にも応用される「サポートベクター回帰」と呼ばれる手法もありますが、分類問題に比べて使用頻度が低いため本記事では割愛します。
■使用するデータ
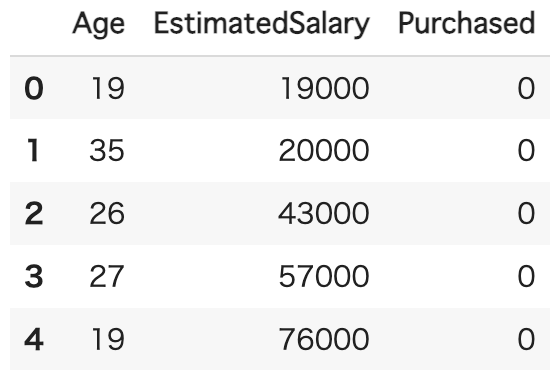
（図１）線形用データ：Social_Network_Ads.csv
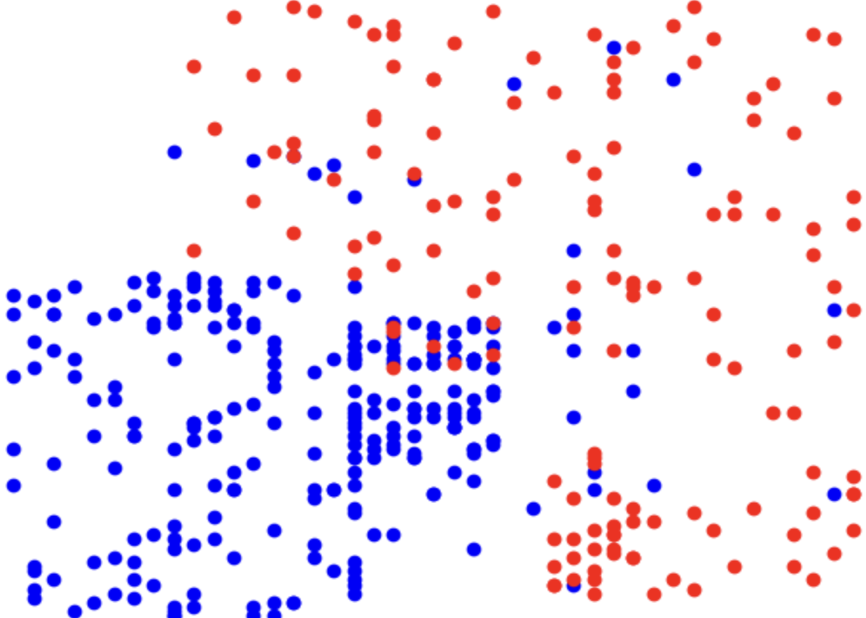
（図２）非線形用データ：gpt_hisenkei.csv
※データセット：後日
データセットのイメージはそれぞれ以下の通り：
■ SVM分析について学習する
上記、赤点と青点を上手に「分類」していく
大まかな流れ）
① データ読み込みや前処理、分割
- 質的変数は用いることができない
② モデルの設定と訓練
- 「SVM」で実施する
③ モデルの精度の確認
- 精度について、以下6項目で確認していく
分類における「学習モデルの性能評価」について確認していく！
(1) 混同行列（confusion matrix）
(2) 正解率（accuracy）
(3) 適合率（precision）
(4) 再現率（recall）
(5) F1スコア（F1-score）
(6) AUC（曲線下面積）
▼復習
※左側が「分類」、右側が「回帰」の例
前回学習したロジスティック回帰では、目的変数が質的の場合に求めていた。いわゆる2択の状態の時。前提情報を用いて、結果を2つに分けることを「分類」と呼ぶ。
対するは、重回帰分析のような、前提情報を用いて数値を予測する場合は「回帰」と呼ぶ。
今まで習ったものや代表的なものをカテゴリ分けすると以下のようになる。
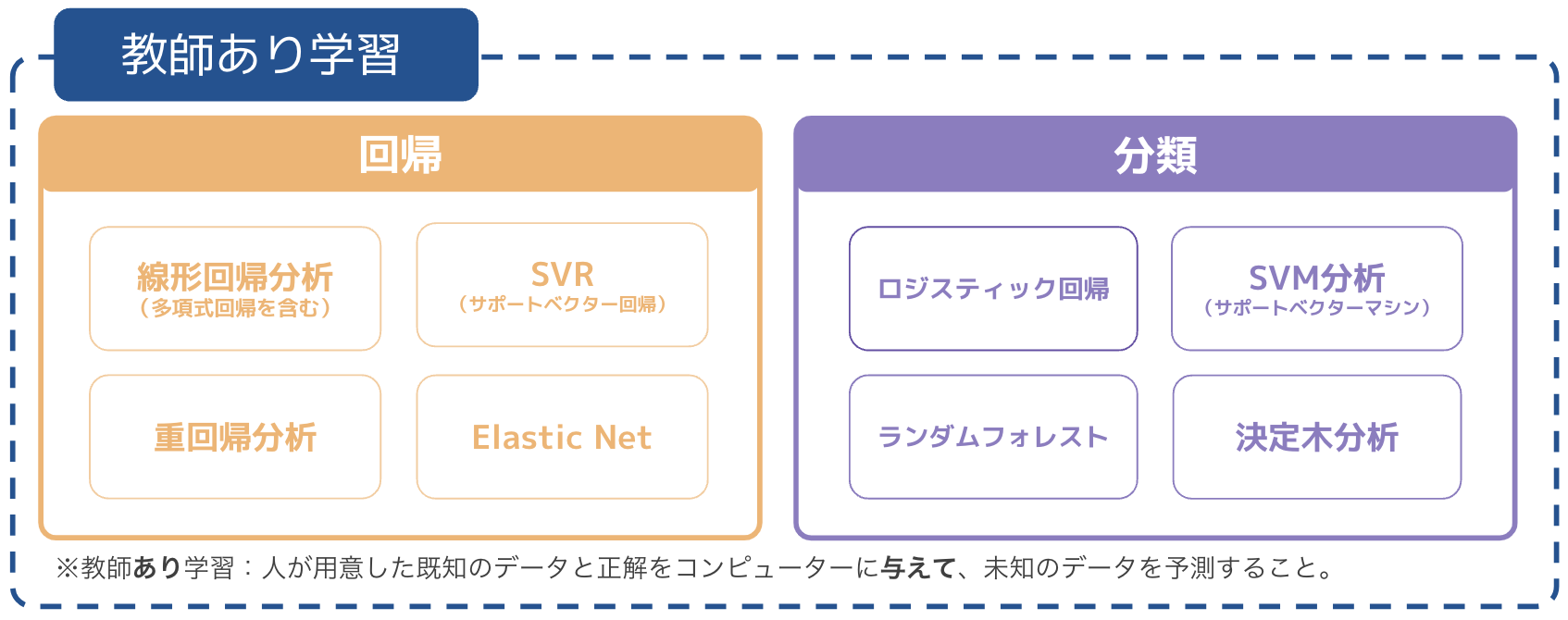
今回は、その中でもよく分類で使われることが多い「SVM（サポートベクターマシン）分析」に焦点を当てていく。
▼SVMとは？
SVMは、複数の説明変数を基に、2つのクラスに分類するための手法である。通常、分類問題に使用される手法だが、回帰問題に対しても拡張して使われることがある。
さて、ここでクイズ！！
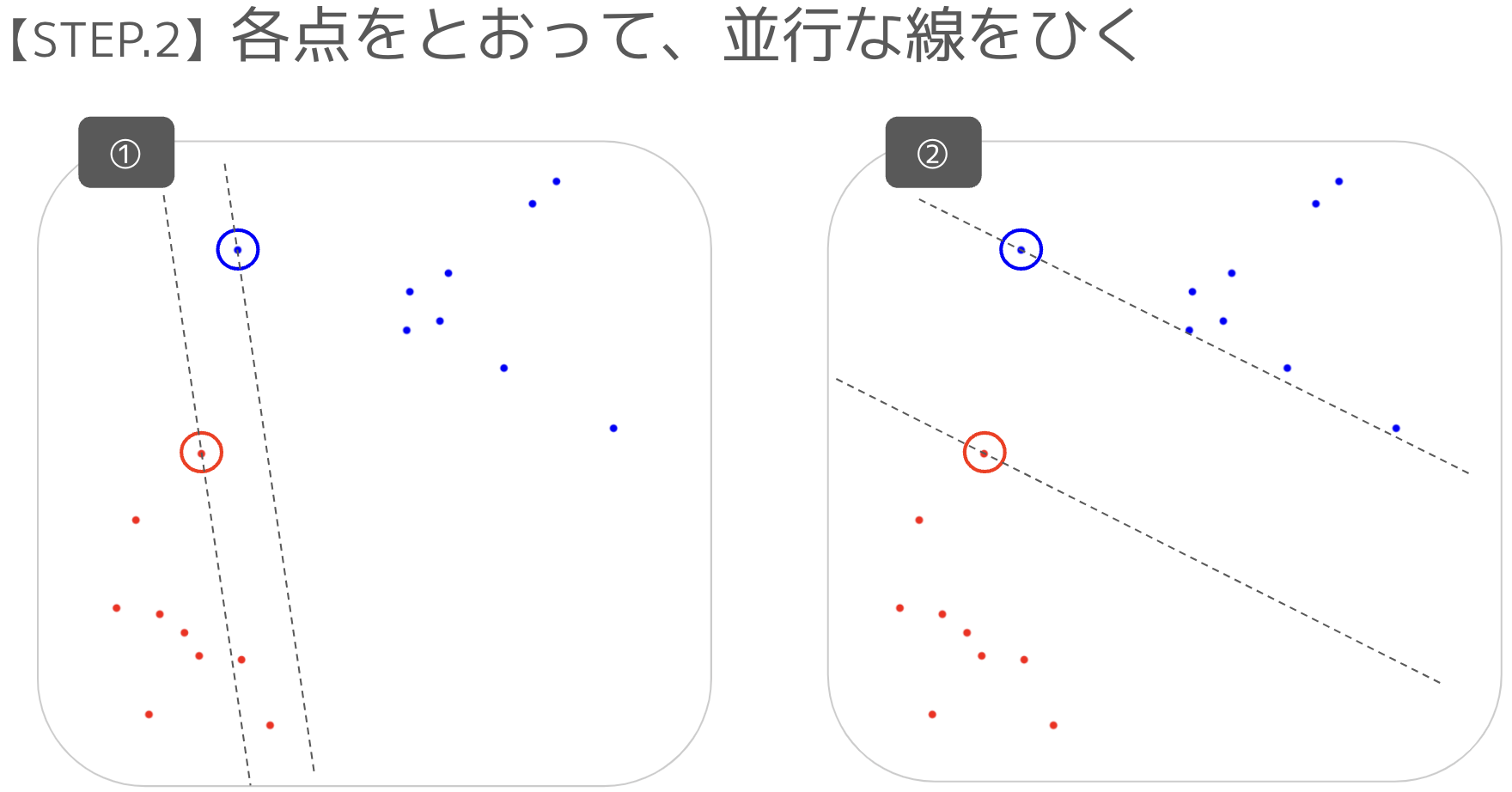
赤色の点の集まりと、青色の点の集まりを分けたく、分割する線を引くことにした。
以下の線は、どちらの方が綺麗に分けられているでしょうか？！
結論、直感的に見ると「②の方が綺麗に分けられていそう」と言える。
こういった線を簡単に引ける方法があれば嬉しい。
→ この均等に分けるための線（モデル）を作るための手法して用いられるものを「SVM（サポートベクターマシン）」と呼ぶ。
ではこれの仕組みを簡単に理解していく。
この手順で、②の分類線を作ることができる。
この線を作成するまでの流れを「SVM」で行うことが可能。
もう少し踏み込んで考えてみる。
今のような、赤点と青線を分けられるものを線形分離可能と呼び、一方で、線形分離不可能なものも存在する。
例として、以下が挙げられる。
上記のオレンジの点、青の点を、一本の直線で分けることは不可である。
ではどのように分類するのか？
結論、以下のように「次元を増やして」分類できるようにしてあげる。
参考：https://www.shoeisha.co.jp/book/article/detail/233
身近な例で見ると、富士山などもそうである。
上から見ると分類線が引けないが、正面から見れば分類線が引ける。
このように、線形分離不可能なものを分けるために次元を増やして考えることをカーネルトリック（カーネル法を用いる）という。
それでは実際に使ってみよう！！
【SVM】
大まかな流れ
① データ読み込みや前処理、分割
- 質的変数は用いることができない
② モデルの設定と訓練
- 「SVM分析」で実施する
- （参照）分類結果のプロット
③ モデルの精度の確認
- 精度について、以下6項目で確認していく
(1) 混同行列（confusion matrix）
(2) 正解率（accuracy）
(3) 適合率（precision）
(4) 再現率（recall）
(5) F1スコア（F1-score）
(6) AUC（曲線下面積）
＜まずは線形用データセットを用いて分析＞
① データ読み込みや前処理、分割
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# データの読み込み
df = pd.read_csv("/content/Social_Network_Ads.csv")
df.head()
〔説明変数〕
・Age（年齢）、EstimatedSalary(お給与)
〔目的変数〕
・Purchased・・・1=購入する、0=購入しない
#説明変数と目的変数に分ける
x = df[["Age","EstimatedSalary"]].values
y = df["Purchased"].values
#データを学習用と検証用に分割
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test = train_test_split(
x,y,train_size=0.7,random_state=0)
#標準化
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
x_train_std = sc.fit_transform(x_train)
x_test_std = sc.transform(x_test)
データの準備完了！
② モデルの設定と訓練
#線形SVMの学習モデル
from sklearn.svm import SVC
model = SVC(kernel = "linear",C=1.0,probability=True,
max_iter=10000,random_state=0)
model.fit(x_train_std,y_train)
パラメータについて
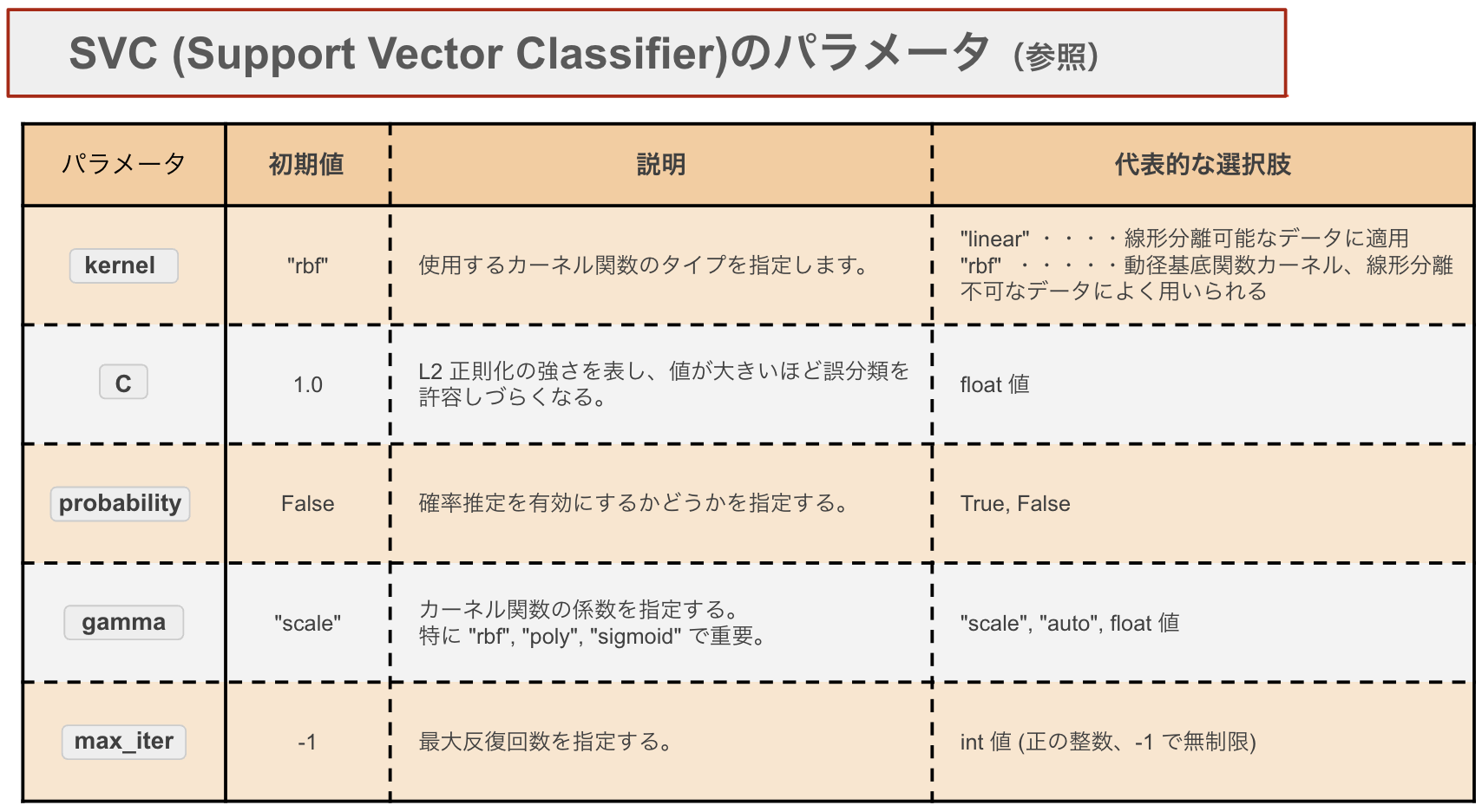
kernelが大事。
線形分離可能な（直線で分けられる）場合はlinearを使い、複雑なデータの場合はrbfを用いることが多い。
※参照：分析結果をプロット
from mlxtend.plotting import plot_decision_regions
x_train_plot = np.vstack(x_train_std)
y_train_plot = np.hstack(y_train)
x_test_plot = np.vstack(x_test_std)
y_test_plot = np.hstack(y_test)
plot_decision_regions(x_test_plot,y_test_plot,clf=model,legend=2)
③ モデルの精度を確認
from sklearn.metrics import confusion_matrix,precision_score,recall_score,f1_score,roc_auc_score
# 混同行列の出力
print("Confusion Matrix:")
print(confusion_matrix(y_true=y_test, y_pred=model.predict(x_test_std)))
# 性能指標の計算と表示
print("正解率(train) =", model.score(x_train_std, y_train))
print("正解率(test) =", model.score(x_test_std, y_test))
print("適合率 =", precision_score(y_true=y_test, y_pred=model.predict(x_test_std)))
print("再現率 =", recall_score(y_true=y_test, y_pred=model.predict(x_test_std)))
print("F1スコア =", f1_score(y_true=y_test, y_pred=model.predict(x_test_std)))
print("AUC =", roc_auc_score(y_true=y_test, y_score=model.predict_proba(x_test_std)[:, 1]))
▼ 回帰式の精度を確認
(1) 混同行列（confusion matrix）
(2) 正解率（accuracy）
(3) 適合率（precision）
(4) 再現率（recall）
(5) F1スコア（F1-score）
(6) AUC（曲線下面積）
＜次に非線形用データセットを用いて分析＞
① データ読み込みや前処理、分割
ここまではほとんど同じ。
② モデルの設定と訓練
#非線形SVMの学習モデル
from sklearn.svm import SVC
model = SVC(kernel = "rbf",gamma=1/2,C=1.0,
probability = True,max_iter=10000,
random_state=0)
model.fit(x_train_std,y_train)
パラメータについて
kernelが大事。
線形分離可能な（直線で分けられる）場合はlinearを使い、複雑なデータの場合はrbfを用いることが多い。
※参照：分析結果をプロット
from mlxtend.plotting import plot_decision_regions
x_train_plot = np.vstack(x_train_std)
y_train_plot = np.hstack(y_train)
x_test_plot = np.vstack(x_test_std)
y_test_plot = np.hstack(y_test)
plot_decision_regions(x_test_plot,y_test_plot,clf=model,legend=2)
③ モデルの精度を確認
from sklearn.metrics import confusion_matrix,precision_score,recall_score,f1_score,roc_auc_score
# 混同行列の出力
print("Confusion Matrix:")
print(confusion_matrix(y_true=y_test, y_pred=model.predict(x_test_std)))
# 性能指標の計算と表示
print("正解率(train) =", model.score(x_train_std, y_train))
print("正解率(test) =", model.score(x_test_std, y_test))
print("適合率 =", precision_score(y_true=y_test, y_pred=model.predict(x_test_std)))
print("再現率 =", recall_score(y_true=y_test, y_pred=model.predict(x_test_std)))
print("F1スコア =", f1_score(y_true=y_test, y_pred=model.predict(x_test_std)))
print("AUC =", roc_auc_score(y_true=y_test, y_score=model.predict_proba(x_test_std)[:, 1]))
▼ 回帰式の精度を確認
(1) 混同行列（confusion matrix）
(2) 正解率（accuracy）
(3) 適合率（precision）
(4) 再現率（recall）
(5) F1スコア（F1-score）
(6) AUC（曲線下面積）
＜まとめ＞
サポートベクターマシン（SVM） は、データを最適に分類する境界線（または超平面）を見つけるための学習モデル。
主に分類タスクに用いられることが多い（回帰で使われることもある）。
カーネルトリックを用いて非線形の問題にも対応することが可能。
以上。
続いては、 決定木へGO！！！