身近なネットワーク
身近にあるネットワークの例として、
➀空港
➁友人関係・SNSのフォロー関係
➂タンパク質の相互作用*
④サイト・論文の引用関係
➄道路網
などがあります。
*Protein-Protein Interactions : PPIと呼ばれる。
この中で➀～④に共通する性質があります。
それは、
・スモールワールド性
・スケールフリー性
の２つです。
スモールワールド性
社会心理学者スタンレー・ミルグラムが1967年に行ったスモールワールド実験によって検証された、「六次の隔たり」で有名です。これは、どんな２人へも平均６人で辿り着くというものです。
例えば、WWWの直径（各サイト間のリンク数の平均値）は約19クリック(Albert al., Nature, 1999)と言われています。
このスモールワールド性を記述するネットワークとして、1998年、ワッツが博士論文のテーマとして、指導教官だったストロガッツとともにスモールワールド・ネットワークを発表しました。これは、WSモデルと呼ばれます。
WSモデル
WSモデルは、
(a)平均頂点間距離𝐿 が小さく、
(b)クラスター係数𝐶 が大きく、
(c) 平均次数⟨𝑘⟩ が大きすぎない（エッジ密度が低い）
ネットワークとして提案されました。
WSモデルによるネットワークの生成手順は以下です。
１．初期状態
𝑛個の頂点を円形状に並べ、すべての頂点が近傍 $𝑘$（偶数）個の頂点との間に辺を持つ。（左右 $𝑘∕2$ 個ずつ）
２．初期状態からある一定の確率$𝑝$でエッジを再接続するという操作を繰り返す。
（ただし、再接続方法は、各頂点$𝑢$に接続しているすべてのエッジに対して、確率$𝑝$でエッジを削除し、エッジの端点を$𝑢+1$から$𝑢−1$の中からランダムに選び再接続する。）
例）$n=10,k=4$の初期状態
再接続確率$p$を変えると、ネットワークの種類が変わります。
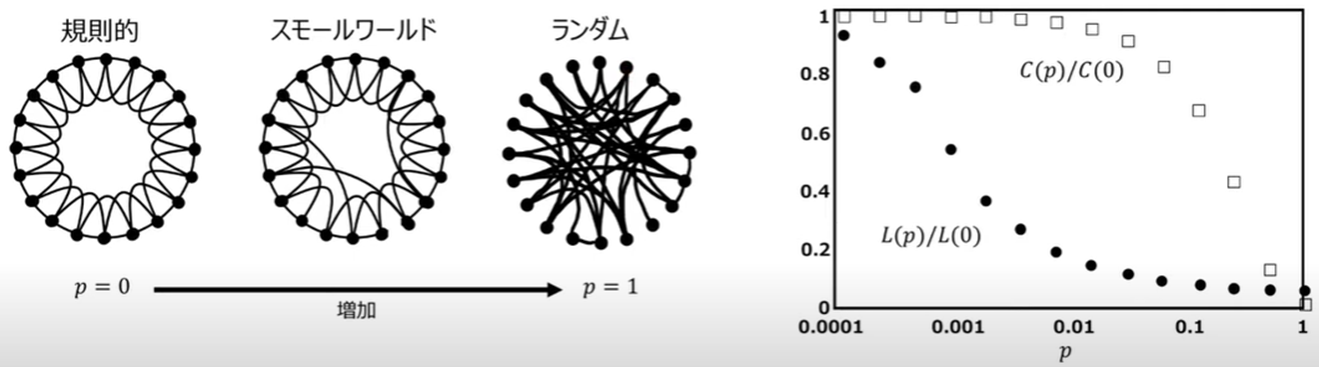上図：再接続確率$p$とネットワークの種類$^*$
*【研究で使うPython】#11 NetworkXによるネットワーク分析 ④スモールワールドネットワークの生成より
WSモデルを用いたネットワーク生成
import networkx as nx
import matplotlib.pyplot as plt
import numpy as np
n = 10 #ノード数
k = 4 #次数
p = 0.1 #リンク繋ぎ変え確率
G1 = nx.watts_strogatz_graph(n,k,p)
pos = nx.circular_layout(G1)
print("クラスター係数",nx.average_clustering(G1))
nx.draw(G1,pos)
plt.show
nx.watts_strogatz_graph(n,k,p)を用いると、WSモデルによるネットワークの生成を行うことができます。再接続確率$p$を大きくすると、クラスタ係数が小さくなることも確認できます。これは、再接続確率が大きくなるほど、ネットワークがランダムに近づくことを意味しています。
再接続確率とクラスタ係数の関係
$n=1000,k=10$の場合の、再接続確率とクラスタ係数の関係をプロットします。
n=1000
k=10
G0=nx.watts_strogatz_graph(n,k,0)
C0=nx.average_clustering(G0)
tmp =np.array(range(1,11))
parray=np.zeros(40)
parray[0:10]=tmp/10000
parray[10:20]=tmp/1000
parray[20:30]=tmp/100
parray[30:40]=tmp/10
result=[]
for p in parray:
G=nx.watts_strogatz_graph(n,k,p)
result.append(nx.average_clustering(G))
result = np.array(result) / C0
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(parray, result, label="Watts Storogatz")
ax.set_xlabel(r'$p$')
ax.set_ylabel(r'$C(p)/C(0)$')
ax.set_ylim(0,1)
ax.set_xscale('log')
plt.legend()
plt.show()
$p$を大きくすると、クラスタ係数が小さくなり、やがて0に近づいてます。
スケールフリー性
スケールフリー性とは、空港やSNSのように、ハブと呼ばれる非常に次数の高い頂点が含まれており、多くの頂点は次数がとても低いという性質です。
スケールフリー性をもつネットワークとしては、
1999年にBarabásiと生徒のAlbertによって考案されたBAモデルが最も基本的です。
BAモデルの重要な要素として、
成長：時間とともに頂点が次々と追加される
優先的探索：次数の高い頂点ほど新しい枝（エッジ）を獲得しやすい
という２つがあります。
BAモデルのルール
➀まず$m_0$個の頂点が完全グラフ$K_{m_0}$をなしている。(初期条件を明確に設けない例も）
➁次に、頂点を一つずつ追加していく。新しい頂点は$m(\leq m_0)$本の枝を持ち、どの頂点と結びつくかは優先的探索で決める。今、頂点が$n$個あり、既存の頂点$v_i (1\leq i \leq n)$が次数$k$をもつとする。そのとき、ある新しい枝が$v_i$に結び付く確率を以下とする。
\Pi (k_i) = \frac{k_i}{\sum_{j=1}^n k_j} \quad (1\leq i \leq n)
上式は、次数に比例する確率で新しい枝が追加されることを意味しています。
BAモデルによって生成したネットワークは、$p(k) \propto k^{-3}$のべき乗則に従うことが知られています。
BAモデルの実装
nx.barabasi_albert_graph(n,m)を用いて、pythonでBAモデルによるネットワーク生成を行うことができます。$n$は頂点数、$m$は１ステップあたりに１つの頂点から追加されるエッジ数です。
import networkx as nx
import matplotlib.pyplot as plt
ba = nx.barabasi_albert_graph(1000,3)
plt.subplot(3,1,1)
nx.draw(ba, node_size=10, node_color="red")
plt.subplot(3,1,2)
plt.plot(nx.degree_histogram(ba))
plt.subplot(3,1,3)
plt.xscale("log")
plt.yscale("log")
plt.grid(which="both")
plt.plot(nx.degree_histogram(ba))
ランダムグラフ
1959年、エルデシュとレニィーによって初めて体系的に導入されました。Erdős–Rényiモデルと呼ばれます。ランダムグラフには、$G(n,m)$型と$G(n,p)$型の２種類あり、一般的には$G(n,p)$型が用いられてきました。
研究者1人ひとりを頂点、共著関係を枝とするネットワークを考えると、ほとんどの研究者はエルデシュから距離5~6以内で繋がっていることから、各研究者のエルデシュからの距離はエルデシュ数とも呼ばれています。
G(n,m)型
ノード数$n$とエッジ数$m$が与えられる．平均次数は$\left< k \right>=\frac{2m}{n}$
例）$n=3,m=2$
各々$\frac{1}{3}$の確率で選ぶ。
G(n,p)型
ノード数$n$，エッジ生成確率$𝑝 $が与えられる．辺の組み合わせは$_nC_2=\frac{n(n-1)}{2}$通りだから，エッジ数の平均は$\left< m\right>=𝑛(𝑛−1)/2 𝑝$ ．平均次数$c=\frac{2\left< m \right> }{𝑛}=(𝑛−1)𝑝$
$p$を$n$に依存して変化させると、グラフの連結性が大きく変わります。（「相転移」と呼ばれる）
Erdős–Rényiモデルを用いたランダムグラフ生成
import networkx as nx
import matplotlib.pyplot as plt
# グラフのノード数と辺の生成確率
n_nodes = 1000 # ノード数
p = 0.3 # 辺が存在する確率
# グラフを生成
G = nx.erdos_renyi_graph(n_nodes, p)
# グラフを描画
nx.draw(G, with_labels=True)
plt.show()
plt.plot(nx.degree_histogram(G))
plt.show()
次数分布はこのようになります。この分布はどのような関数でしょうか。
ランダムグラフG(n,p)の次数分布
頂点は他の$n-1$個の頂点と確率$p$で結ばれるため、次数が$k$となる確率$p_k$は、
p_k = _{n-1}C_k \cdot p^k \cdot (1-p)^{n-1-k}
となります。$n$が十分大きい場合は、
p_k \simeq \frac{(n-1)^k}{k !}p^k e^{-c} = \frac{c^k}{k!}e^{-c}
となり、ポアソン分布に従います。ただし、平均次数$c=(n-1)p$を用いました。
ここで、クラスター係数は、$C=p=c/(n-1)$は、$n$が大きいほど0に近づきます。
クラスター係数は、友達の友達が友達である確率
現実の社会ネットワークではクラスタ係数がある程度大きいことが知られているため、ランダムグラフはその現象を記述できていないといえます。
様々なグラフと次数分布
$n=100$の４つのネットワークにおける次数分布を比較してみましょう。
以下は、左から➀ランダムグラフ、➁スケールフリーネットワーク、③完全グラフ、④実在するネットワーク（米国の大学の空手クラブの交友ネットワーク）です。
ここで、これらの次数分布は、
➀ランダムグラフ・・・二項分布（ポアソン分布）
➁スケールフリーネットワーク・・・冪分布
➂完全グラフ・・・すべてのノードの次数が99
④社会ネットワーク・・・？？？
社会ネットワークは、次数分布を記述することはできませんが、①～③のどれに近いかは一目瞭然です。
➁のBAモデルによるスケールフリーネットワークは、現実の社会ネットワークをうまく記述しているのがわかります。
import networkx as nx
import matplotlib.pyplot as plt
er = nx.erdos_renyi_graph(100,0.1)
plt.subplot(241)
nx.draw(er, node_size=10, node_color="red")
plt.subplot(245)
plt.plot(nx.degree_histogram(er))
ba=nx.barabasi_albert_graph(100,3)
plt.subplot(242)
nx.draw(ba, node_size=10, node_color="red")
plt.subplot(246)
plt.plot(nx.degree_histogram(ba))
K_100 = nx.complete_graph(100)
plt.subplot(243)
nx.draw(K_100, node_size=10, node_color="red")
plt.subplot(247)
plt.plot(nx.degree_histogram(K_100))
karate = nx.karate_club_graph()
plt.subplot(244)
nx.draw(karate, node_size=10, node_color="red")
plt.subplot(248)
plt.plot(nx.degree_histogram(karate))
コード参考：村田剛志「Pythonで学ぶネットワーク分析」
本記事を書くにあたり、この方の記事を一部参考にさせていただきました。
参考文献
・村田剛志「Pythonで学ぶネットワーク分析」