はじめに
グラフ理論における媒介中心性を、実際の都市の道路網に適用してみます。これによって、車・人通りの多いポテンシャルを持つエリアを簡単に可視化することができます。
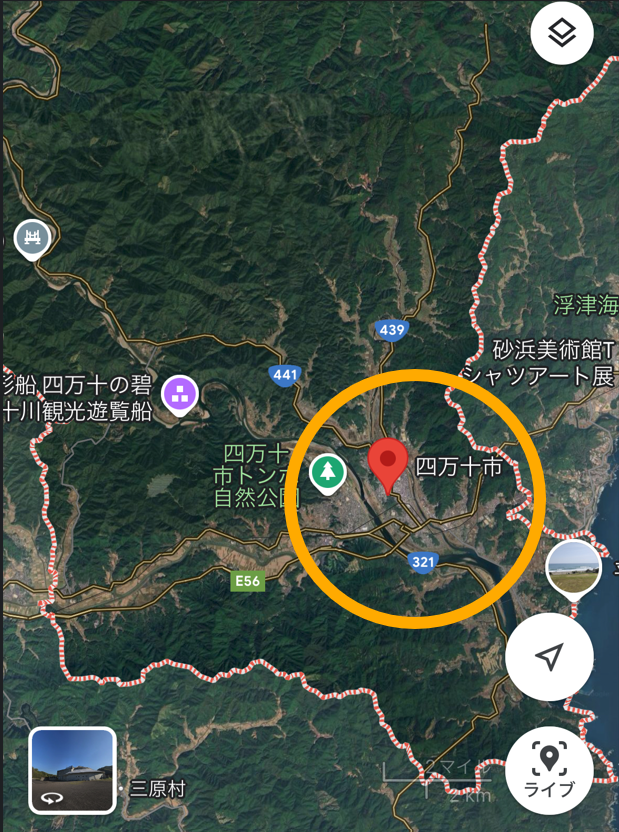
上図は、高知県四万十市。
媒介中心性とは
ノード$i$の媒介中心性とは、すべてのノードのペア$(s,t)$の最短経路のうち、ノード$i$を通る経路の数と定義されいます。
*最短経路が$k$本ある場合は、経路上のノードに対してそれぞれ$1/k$の中心性を付与するなどもあります。
媒介中心性は、ネットワーク上で「そのノードを通るフローがどれほどあるか」を示しており、そのノードの重要性・中心性を表す指標の一つになっていると言えます。
例えば、下図のノードAは次数中心性(そのノードの次数)は低いが、媒介中心性が高い典型的な例です。
Group間の移動には必ずAを通らなければいけません。
Pythonでのコード
対象地域の道路情報を取得し、道路ネットワークを可視化
import folium
import osmnx as ox
# 対象地域の道路情報取得 (例:高知県四万十市)
query = "Shimanto,Kochi,Japan"
G = ox.graph_from_place(query, network_type="drive")
# 道路グラフネットワーク可視化
fmap = ox.plot_graph_folium(G)
fmap.save(outfile="road_network.html")
opts = {"node_size": 5, "bgcolor": "white", "node_color": "blue", "edge_color": "blue"}
ox.plot_graph(G, show=False, save=True, filepath="road_network.png", **opts)
すると、以下のように道路網ネットワークが出力されます。
各ノードの媒介中心性を計算
NetworkXというPythonのネットワーク分析パッケージを用いると、nx.betweeness_centralityによって簡単に媒介中心性を求められます。
# betweenness centralityの計算
betweenness_centrality = nx.betweenness_centrality(G)
print(betweenness_centrality)
媒介中心性をヒートマップとして可視化
媒介中心性が大きいノードほど赤く、大きくなるようにします。ネットワークの種類やサイズによって、node_sizesの500の部分は変えても良いかと思います。
# ヒートマップ表示のためのノード中心性の値を取得
node_centrality_values = list(betweenness_centrality.values())
node_positions = list(betweenness_centrality.keys())
# ノードのサイズと色を媒介中心性に基づいて設定
node_sizes = [v * 500 for v in betweenness_centrality.values()]
node_colors = [v for v in betweenness_centrality.values()]
# 道路グラフネットワーク可視化
fmap = ox.plot_graph_folium(G)
fmap.save(outfile="road_network.html")
opts_heatmap = {"node_size": node_sizes, "bgcolor": "white", "node_color": node_colors, "edge_color": "blue"}
ox.plot_graph(G, show=False, save=True, filepath="road_network_Shimanto.png", **opts_heatmap)
実行すると、以下のような出力が得られます。
右下の密集したエリアにヒートマップが集中しているのがわかります。
そして、Google Mapで実際に四万十市の衛星写真を見てみると、媒介中心性が高く表示されていたエリアと市街地がおおよそ一致しているのがわかります。
まとめ
今回は、グラフ理論の媒介中心性を用いて、都市の道路網における重要性をヒートマップとして可視化してみました。非常に簡単で、単純な理論やプログラムですが、割と現実と一致しているという興味深い結果が得られました!
より高度な分析には、Space Syntax理論という理論を用いたものもあります。それについての記事も書いていますので、ぜひそちらもご覧下さい。
-
Newman, M. (2018). Networks. Oxford university press. ↩



