Space Syntax理論とは ー道路網・建築における空間構造分析ー

はじめに

道路ネットワークや建築分野などに用いられるSpace Syntax理論についてまとめました。

↑このような地図の作成方法については別記事でまとめています。本記事の一番下にリンクがあるので、ぜひそちらもご覧ください。

Space Syntaxとは

Space Syntax（SS理論）とは、建築や道路などにおける空間構成を分析する手法・学問のことです。建築家のBill Hillier氏が1989年に『The social logic of space』の中で提案したのが始まりです。

芸術として捉えられることが多かった建築に、普遍的で理論的な側面をもたらそうとしたのが彼のきっかけです。

Space Syntaxとは簡単に、空間構造の分析、すなわち「空間の構成がどのようになっているか」「ある空間がどれほどアクセスしやすいところor入り組んだところにあるか」などを分析する手法です。

Space Syntaxは位相幾何学（トポロジー）のように、長さや大きさに意味はなく、構造にのみ興味がある分野です。

分析手順

以下は、Space Syntaxを用いた分析手順の例です。

例1：道路網

¹
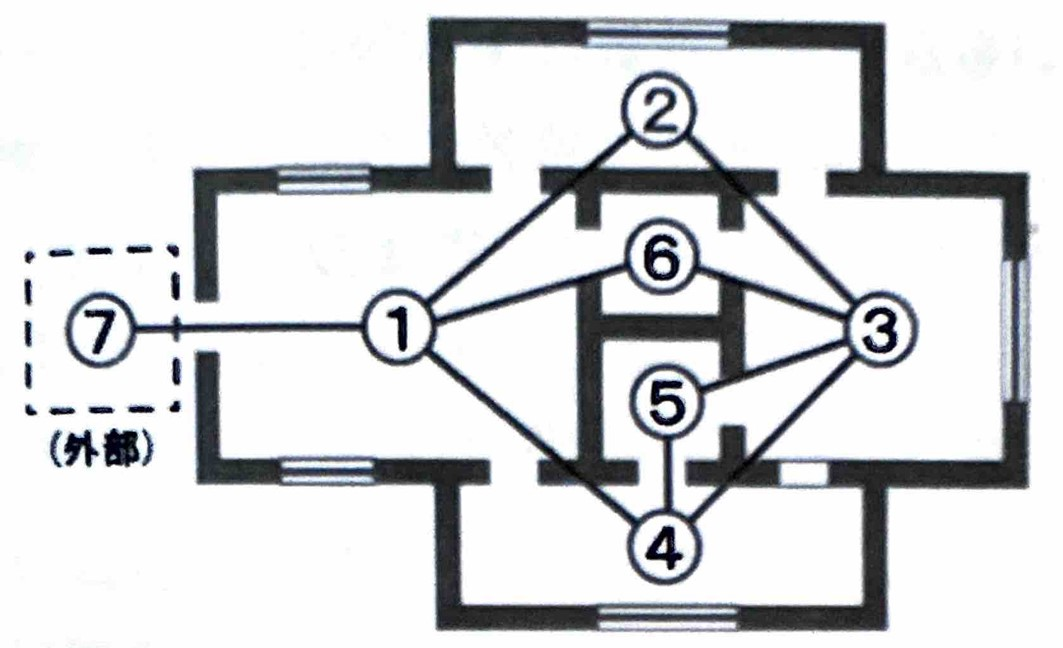
左から(a)架空都市、(b)axial map、(c)connectivity graph、(d)justified graph

(a)→(b)

まず、道路を直線で表現したグラフ (axial map) を作成します。

(b)→(c)

エッジをノード（点）に変換したグラフを作成します。

例えば、上図(b)の辺１は辺２，３，４，５という４本の辺と繋がっているため、(c)では、点１には点２，３，４，５が隣接しています。

(c)→(d)

最後に、ある着目したい一点を一番下に配置して、✚マークを付けます。
この点を根 (root) と呼びます。他の点は番号に意味はないため、番号は取ります。
一番右(d)のグラフをj-グラフと呼びます。

例2：部屋

部屋の空間構造にも、同様に当てはめることができます。

²
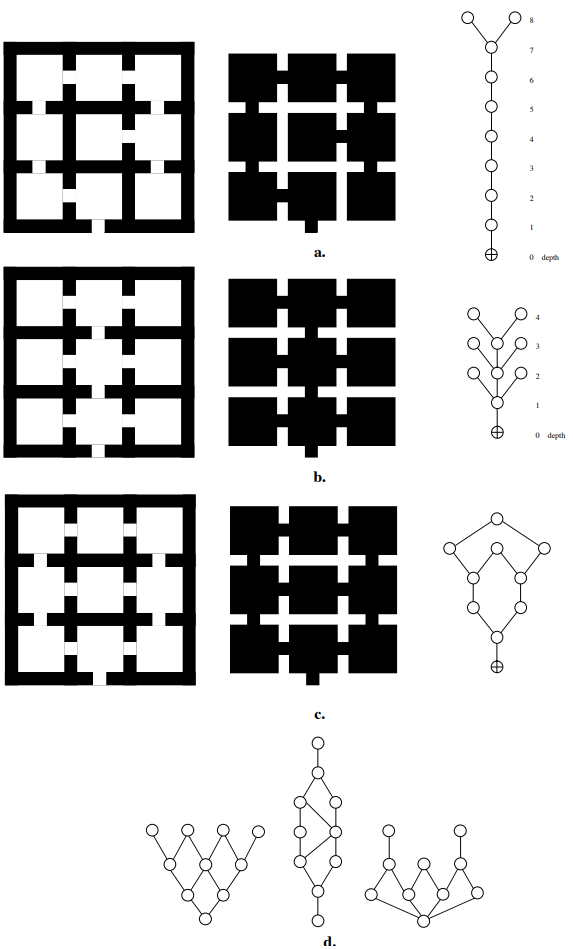
上図には、a,b,cの３種類の住宅モデル（一番左）があります。どれも3×3の9個の部屋と9個のドアを持つ同じ形状の住宅ですが、よく見るとドアの場所が異なります。

このドアの配置の違いが空間構造に大きな違いをもたらします。
建物のない空間を取り出し、（上図中央）道路網の場合と同じように、部屋をノード、ドア（部屋の結合）をエッジとするグラフに変換します。その後、外部空間を根とするj-グラフ（上図右）に変換します。

ここで、空間（ここでは道路）構造を測る指標として、

• Connectivity
• Control Value
• Depth（深度）
• RA (Relative Asymmetry)
• RRA (Real Relative Asymmetry)
• Integration（統合度）
  などがあります。

これらの各指標の定義についてまとめます。

Space Syntaxにおける各指標の定義

以下の部屋のレイアウト³を例に考えてみましょう。
³

＊以下、頂点は空間のことを指しています。

Connectivity

頂点に直接接続された近傍頂点の個数。例えば、頂点➀のConnectivityは4.

Control Value

近傍空間の Connectivity の逆数和。頂点➀におけるControl Valueは、

\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{3}=\frac{11}{6}

この指標は、近傍頂点の次数 (Connectivity)が小さいほど、近傍頂点数が多いほど大きくなることから、ある頂点がグラフ内でどの程度「支配的」であるかと解釈できます。

Depth（深度）

ある頂点から他の頂点に到達するのに必要な最小ステップ数。
例えば、頂点➀から頂点➂へのdepthは2.

中でも、ある頂点$i$から他のすべての空間までのdepthの総和を$TD_{i}$ (Total Depth)といいます。
例えば、頂点5におけるdepthの総和$TD_{5}$は、距離×頂点数の和として、

TD_{5} = 1 ×2 + 2×3 + 3×1 =11

と計算できます。

グラフ理論では、距離の総和$TD_{i}$の逆数は、近接中心性と呼ばれることがあります。

また、グラフの頂点数を$n$とすると、頂点$i$からのdepthの平均$MD_{i}$ (Mean Depth) は、頂点$i$以外の$(n-1)$個の頂点までの距離の総和$TD_{i}$を用いて、

MD_{i} = \frac{TD_{i}}{n-1}

と求められます。

上式は、グラフの頂点数$n$と頂点$i$の位置に依存します。そこで、SS理論では、これらを$0～1$の値になるように相対的なRA値 (Relative Asymmetry Value)に変換します。

RA (Relative Asymmetry)

RAとは、相対的非対称度といい、対象とする地域全体から見た、その空間から相対的な深さを表しています。この値が大きいほど、相対的に深く、入り組んだとことであると言えます。

RAの計算には、depthの平均$MD_{i}$の最小値と最大値を用います。まず、頂点数$n$
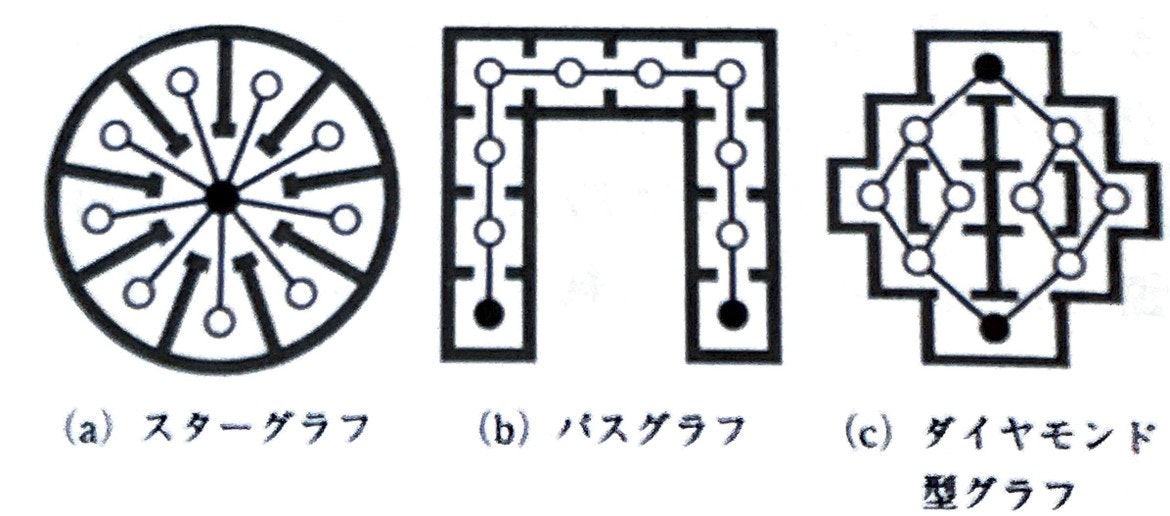
の様々なグラフの中で、$MD_{i}$が最小となるのは、下図(a)のスターグラフの中央の頂点の場合。中央の頂点から他のすべての頂点まではdepthが1なので、$MD_{i}$の最小値$\min MD_{n}$は$1$となります。

一方、$MD_{i}$が最大となるのは、下図(b)のパスグラフの端点の場合。部屋が直線状に並んだとき、端部の部屋が最も移動効率が悪いことは直感的にも理解できます。端点における距離の総和$TD_{i}$は$n(n-1)/2$なので、$MD_{i}$の最大値 $\max MD_{n}$は、$n/2$となります。

³

どんな$n$においても、スターグラフの中央の頂点で平均深度$MD$は最小で、パスグラフの端点で最大になります。

上記のmin $MD_{n}$とmax $MD_{n}$を用いると、頂点$i$のRA値は

RA_{i} =\frac{MD_{i} - \min MD_{n}}{\max MD_{n} - \min MD_{n}} = \frac{2(MD_{i}-1)}{n-2}

と求められます。この式を利用すると、例えば頂点➄の$RA_{5}$は、

RA_{5} = \frac{2(MD_{5}-1)}{7-2} = 0.333

と計算できます。RA値は$0～1$の値なので、グラフの頂点間の値を比較しやすい指標になっています。ただ、規模が異なる他のグラフと比較する際にはあまり適していません。

そこで、頂点数$n$の影響を受けないようにRRA値 (Real Relative Asymmetry Value)として、$D_{n}$という値を用いて標準化します。

RRA値

RRAとは、RAから対象領域の規模による影響を取り除いた数値であり、他の対象領域と比較可能にするために標準化した値です。

D_{n} = \frac{2[n(\log_2 (\frac{n+2}{3})-1)+1]}{(n-1)(n-2)}

$D_{n}$は、$n$個の頂点が上図(c)のようなダイヤモンド型グラフのとき、depthが最大となる頂点（図中の●）のRA値。

頂点$i$のRRA値はRA値を$D_{n}$で除して標準化し、

RRA_{i} = \frac{RA_{i}}{D_{n}}

と定義されます。したがって、頂点➄の$RRA_{5}$は、

RRA_{5} = \frac{RA_{5}}{D_{7}} =\frac{0.333}{0.340} = 0.981

となります。RRA値が小さいほど、そのグラフの頂点の中心性が高いと解釈できます。

Integration (統合値、Int値）

RRA値の逆数であるIntegrationという指標も良く用いられます。逆数にするのは、値が大きいほど中心性も高いという感覚に合わせるためです。

Int_{i} = \frac{1}{RRA_{i}} = \frac{n[\log_2 (\frac{n+2}{3})-1]+1}{(MD_{i}-1)(n-1)}

➀Int値が大きい

移動距離が短く、アクセスが容易。つながりが強い。統合 (integrate) されている。
例）リビング

➁Int値が小さい

移動距離が長くアクセスが困難。つながりが弱い。分離 (segregate) されている。
例）家の外

Int値にはグローバルとローカルがあります。グラフのすべての頂点からのdepthを計量の範囲とする場合をグローバルレベル、グラフの各頂点からのdepthを限定した場合をローカルレベルといいます。

Int値は、空間構成の「中心/周縁」、「近接/遠隔」を表す指標になっています。

まとめ

今回は、空間構造の分析手法であるSpace Syntaxについてまとめました。実際の都市空間に適用して分析する手順についてもまとめたので、そちらもぜひご覧ください。

1. 画像：Dettlaff, W. (2014). Space syntax analysis–methodology of understanding the space. PhD Interdisciplinary Journal, 1, 283-291.
   引用元原論文：Jiang, B., & Claramunt, C. (2002). Integration of space syntax into GIS: new perspectives for urban morphology. Transactions in GIS, 6(3), 295-309. ↩

2. Hillier, B. (2007). Space is the machine: a configurational theory of architecture. Space Syntax. ↩

3. 貞広幸雄,山田育穂, 石井儀光 他. (2022). 空間解析入門 都市を測る・都市がわかる. 朝倉書店, 第4刷. ↩ ↩² ↩³