※本記事は Classi Advent Calendar 2020 の2日目の記事です
みなさん、こんにちは。Classi データAI部 データサイエンティストの廣田と申します。
ある日の社内輪読会でハミング符号の話が登場し、面白そうだったのでnumpyで実装してみました。本記事ではその内容をご紹介したいと思います。
本記事の概要
- (7, 4)ハミング符号をnumpyで実装
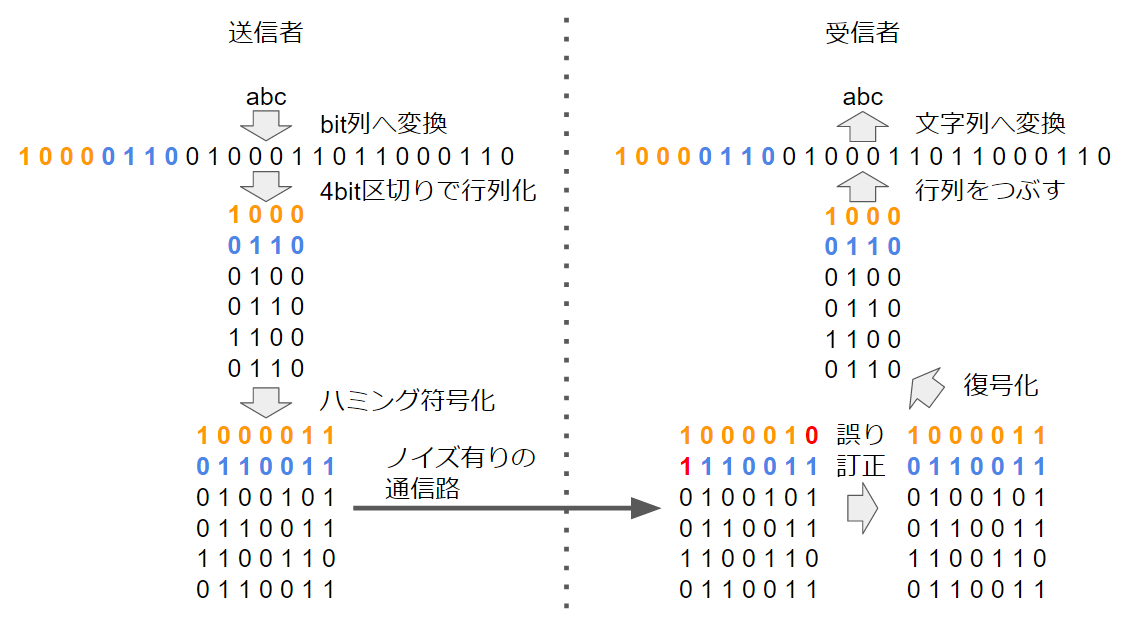
- 本記事で実装する処理の全体像は下記の図の通りです
ハミング符号概説
- 2値線形ブロック符号のひとつ
- 1ブロックあたり1ビットの誤りを検出・訂正できます
実装
まず本記事の概要にある図を見てください。上の方に書いてある処理から順に実装していき、最後に全処理をつなぎ合わせます。
GF(2) 上における計算方法について
ハフマン符号化・復号化では2元ガロア体 GF(2) 上のベクトル・行列の加法・乗法が必要となってきます。この計算方法ですが、通常の計算結果を求めた後で2で割った余りを求めれば良いです。pythonであれば % 2 するだけでOKです。
文字列とbit列、bit列とbit行列の間の変換
まず文字列とbit列の間の変換の実装例を示します。逆方向の計算を組み合わせることで元の文字列に戻ることを確認しておきましょう。
import numpy as np
def str2bits(input_str):
bits = [1 << i for i in range(8)]
return np.array([1 if ord(char) & b > 0 else 0 for char in input_str for b in bits])
def bits2str(input_bits):
bits = [1 << i for i in range(8)]
return ''.join(chr(
sum(b * ib for b, ib in zip(bits, input_bits[i:i+8]))
) for i in range(0, len(input_bits), 8))
print(str2bits('abc'))
# -> [1 0 0 0 0 1 1 0 0 1 0 0 0 1 1 0 1 1 0 0 0 1 1 0]
print(bits2str(str2bits('abc')))
# -> abc
次にbit列とbit行列の間の変換の実装例を示します。こちらも同様に、逆方向の計算を組み合わせることで元のbit列に戻ることを確認しておきましょう。
import numpy as np
def bits2mat(bits, n_cols=4):
n_rows = len(bits) // n_cols
mat = np.zeros((n_rows, n_cols), dtype=np.int)
for i in range(n_rows):
for j in range(n_cols):
if bits[i * n_cols + j] > 0:
mat[i, j] = 1
return mat
def mat2bits(mat):
n_rows, n_cols = mat.shape
return [mat[i, j] for i in range(n_rows) for j in range(n_cols)]
print(bits2mat(np.array([0, 0, 0, 0, 1, 1, 1, 1])))
# -> [[0 0 0 0]
# [1 1 1 1]]
print(mat2bits(bits2mat(np.array([0, 0, 0, 0, 1, 1, 1, 1]))))
# -> [0, 0, 0, 0, 1, 1, 1, 1]
ハミング符号化・復号化
ハミング符号化には生成行列 $G$ が必要となります。$G$ の具体的な値は下記の実装例をご覧ください。ハミング符号化前のbit行列 $X$ をハミング符号化したものは $XG$ となります。生成行列の取り方は何通りか存在しますので、気になる方は調べてみてください。
ハミング復号化には生成行列 $G$ と $$GR = I(単位行列)$$ という関係にある行列 $R$ を準備すると便利です。ハミング符号化済みのbit行列を $C$ とすると、ハミング復号化したものは $CR$ となります。ちなみにbit行列 $X$ をハミング符号化・復号化すると、行列 $R$ の定め方から
$$ XGR = XI = X $$
が成り立ち、元に戻ることがわかります。これで復号化処理がきちんと機能することが確認できました。
ここでハミング符号化・復号化の実装例を示しておきます。numpyであれば行列をかけて2で割った余りを求めればOKです。符号化・復号化を組み合わせることで元のbit行列に戻ることを確認しておきましょう。
import numpy as np
def encode(mat):
G = np.array([
[1, 0, 0, 0, 0, 1, 1],
[0, 1, 0, 0, 1, 0, 1],
[0, 0, 1, 0, 1, 1, 0],
[0, 0, 0, 1, 1, 1, 1]
])
return np.dot(mat, G) % 2
def decode(encoded_mat):
R = np.array([
[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1],
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]
])
return np.dot(encoded_mat, R) % 2
print(encode(np.array([[0, 1, 0, 1], [1, 1, 1, 1]])))
# -> [[0 1 0 1 0 1 0]
# [1 1 1 1 1 1 1]]
print(decode(encode(np.array([[0, 1, 0, 1], [1, 1, 1, 1]]))))
# -> [[0 1 0 1]
# [1 1 1 1]]
誤り訂正
誤り訂正には検査行列 $H$ を利用します。この行列は生成行列 $G$ と
H G^{\top} = O \\
G H^{\top} = O
といった関係にある行列です。$H$ の具体的な値については下記の実装例をご覧ください。ここで、この検査行列を用いてどう誤りを検出・訂正するのか説明してみます。
いきなり行列で考えると議論が複雑になるので、行ベクトル $x$ をハミング符号化することを考えます。行ベクトル $x$ をハミング符号化したもの $c = xG$ を考えます。これをノイズ有りの通信路に通すと、受信者側ではノイズベクトル $e$ が乗った $\tilde{c} = c + e = xG + e$ を受け取ることになります。
ここで、受信者側が受け取ったベクトルに検査行列(の転置行列)をかけた量
$$ (xG + e) H^{\top} = xGH^{\top} + eH^{\top} = xO + eH^{\top} = eH^{\top} $$
を考えます。この量はシンドロームと呼ばれています。もしノイズが全く乗らなければ $e = 0$ なので、シンドロームも $0$ となります。しかしノイズがある場合はシンドロームは $0$ とは限りません。誤りが高々1ヵ所であるという仮定を置けば、ノイズがあることとシンドロームが $0$ でないことは同値です。したがって、シンドロームが $0$ か否かで誤りの有無が判定できるわけです。
シンドロームが $0$ でない場合、どのように誤りを訂正すればよいのでしょうか?前述の仮定を踏まえ、ノイズベクトル $e$ の $j$ 番目の要素だけ1・その他の要素は0というケースを考えてみます。これは $j$ 番目の要素に誤りがあるケースを考えていることになります。この時 $eH^{\top}$ は $H^{\top}$ の第 $j$ 行($H$ の第 $j$ 列)となります。これを逆に考えれば、シンドロームの値が $0$ でない場合、その値が $H^{\top}$ のどの行と一致するか($H$ のどの列と一致するか)で誤り箇所を特定できます。つまりノイズベクトル $e$ が求められることになります。ノイズベクトル $e$ が求まれば、受信者側は $\tilde{c} + e$ とすれば誤り訂正ができます。というのも、ここで考えているベクトルは全て GF(2) 上のベクトルで $e + e = 0$ が成り立っており、
$$ \tilde{c} + e = (xG + e) + e = xG + (e + e) = xG + 0 = xG $$
が成立するためです。
以上のことをまとめると、受信者が受け取ったbit行列の各行に対して誤りが高々1ヵ所であるという仮定の下で下記のような手順で誤り訂正が実現できます:
- 受信者が受け取ったbit行列の各行 $\tilde{c}$ に対して下記処理を行う
- シンドローム $\tilde{c}H^{\top}$ を計算
- シンドロームが $0$ ならノイズなし
- シンドロームが $0$ でない場合
- 検査行列の転置行列 $H^{\top}$ のどの行と一致するか調べる(第 $j$ 行と一致したとする)
- $\tilde{c} + e_{j}$ で誤りを訂正($e_{j}$: $j$ 番目の要素だけ1で他は0のベクトル)
ここでノイズを求める処理の実装例を示します。 find_error_mat の実行結果を見てみると、確かに符号化した値に乗せたノイズを復元できていることがわかります。誤り訂正をしたい場合は、ここで求めたノイズを受信者が受け取ったbit行列に足せばOKです。
import numpy as np
def find_error(encoded_vec):
H = np.array([
[0, 1, 1, 1, 1, 0, 0],
[1, 0, 1, 1, 0, 1, 0],
[1, 1, 0, 1, 0, 0, 1]
])
syndrome = np.dot(encoded_vec, H.T) % 2
n_column = H.shape[1]
for column in range(n_column):
if np.all(H[:, column] == syndrome):
error = np.zeros(n_column, dtype=np.int)
error[column] = 1
return error
return np.zeros(n_column, dtype=np.int)
def find_error_mat(encoded_mat):
return np.apply_along_axis(find_error, 1, encoded_mat)
encoded_mat = np.array([
[0, 1, 0, 1, 0, 1, 0],
[1, 1, 1, 1, 1, 1, 1]])
print(find_error_mat(encoded_mat))
# -> [[0 0 0 0 0 0 0]
# [0 0 0 0 0 0 0]]
encoded_mat[0, 0] = (1 + encoded_mat[0, 0]) % 2
encoded_mat[1, 2] = (1 + encoded_mat[1, 2]) % 2
print(find_error_mat(encoded_mat))
# -> [[1 0 0 0 0 0 0]
# [0 0 1 0 0 0 0]]
すべて繋げて誤り訂正できるかテスト
ノイズ有りの通信路は、符号化後のbit行列の各要素の0-1をランダムに逆転させることで実現が可能です。この通信路も付け加えた上で、これまで用意した要素を全部つなぎ合わせてみましょう。
import numpy as np
def str2bits(input_str):
bits = [1 << i for i in range(8)]
return np.array([1 if ord(char) & b > 0 else 0 for char in input_str for b in bits])
def bits2str(input_bits):
bits = [1 << i for i in range(8)]
return ''.join(chr(
sum(b * ib for b, ib in zip(bits, input_bits[i:i+8]))
) for i in range(0, len(input_bits), 8))
def bits2mat(bits, n_cols=4):
n_rows = len(bits) // n_cols
mat = np.zeros((n_rows, n_cols), dtype=np.int)
for i in range(n_rows):
for j in range(n_cols):
if bits[i * n_cols + j] > 0:
mat[i, j] = 1
return mat
def mat2bits(mat):
n_rows, n_cols = mat.shape
return [mat[i, j] for i in range(n_rows) for j in range(n_cols)]
def encode(mat):
G = np.array([
[1, 0, 0, 0, 0, 1, 1],
[0, 1, 0, 0, 1, 0, 1],
[0, 0, 1, 0, 1, 1, 0],
[0, 0, 0, 1, 1, 1, 1]
])
return np.dot(mat, G) % 2
def decode(encoded_mat):
R = np.array([
[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1],
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]
])
return np.dot(encoded_mat, R) % 2
def find_error(encoded_vec):
H = np.array([
[0, 1, 1, 1, 1, 0, 0],
[1, 0, 1, 1, 0, 1, 0],
[1, 1, 0, 1, 0, 0, 1]
])
syndrome = np.dot(encoded_vec, H.T) % 2
n_column = H.shape[1]
for column in range(n_column):
if np.all(H[:, column] == syndrome):
error = np.zeros(n_column, dtype=np.int)
error[column] = 1
return error
return np.zeros(n_column, dtype=np.int)
def find_error_mat(encoded_mat):
return np.apply_along_axis(find_error, 1, encoded_mat)
def main():
np.random.seed(0)
input_str = 'I tried Hamming code implementation with numpy. Does it work well?'
for error_rate in [0.01, 0.02, 0.03, 0.04, 0.05]:
# 符号化する
input_hamming_code = encode(bits2mat(str2bits(input_str)))
# ノイズありの通信路を通す
noise_added_hamming_code = (input_hamming_code + np.random.choice(
[0, 1], input_hamming_code.shape, p=[1 - error_rate, error_rate])) % 2
# 比較のために誤り訂正なしで復号化してみる
not_corrected_result = bits2str(mat2bits(decode(noise_added_hamming_code)))
# 誤り訂正した上で復号化
corrected_hamming_code = noise_added_hamming_code + find_error_mat(noise_added_hamming_code)
result = bits2str(mat2bits(decode(corrected_hamming_code)))
# 結果表示
print(f'*** 誤り発生率 {error_rate} の通信路の場合 ***')
print(f'入力 : {input_str}')
print(f'誤り訂正無しの復号結果: {not_corrected_result}')
print(f'誤り訂正有りの復号結果: {result}')
if __name__ == '__main__':
main()
いざ実行…
$ python hamming.py
*** 誤り発生率 0.01 の通信路の場合 ***
入力 : I tried Hamming code implementation with numpy. Does it work well?
誤り訂正無しの復号結果: I tried Ha-ming!code implementctaoj with nemxy. Does iô work well?
誤り訂正有りの復号結果: I tried Hamming code implementation with numpy. Does it work well?
*** 誤り発生率 0.02 の通信路の場合 ***
入力 : I tried Hamming code implementation with numpy. Does it work well?
誤り訂正無しの復号結果: I tRied Hamming code empleíefpation with îumpy. doas iô work well?
誤り訂正有りの復号結果: I tried Hamminf code gmplementation with numpy. Does it work well?
*** 誤り発生率 0.03 の通信路の場合 ***
入力 : I tried Hamming code implementation with numpy. Does it work well?
誤り訂正無しの復号結果: I triåd HammiLg code )mXlemeîtatioî whth numpy. D-M3 it wOrk sell?
誤り訂正有りの復号結果: I tried Hamming code implementation with numpy. Does it work well?
*** 誤り発生率 0.04 の通信路の場合 ***
入力 : I tried Hamming code implementation with numpy. Does it work well?
誤り訂正無しの復号結果: I drH%d laMming cde im0mei%ntatiOn3wiÔxo}mpy. DoEs¤it worj weld?
誤り訂正有りの復号結果: I dried Hamming code implementatiol'wiÔh numpy. Does it work well?
*** 誤り発生率 0.05 の通信路の場合 ***
入力 : I tried Hamming code implementation with numpy. Does it work well?
誤り訂正無しの復号結果: I tryed0Jamming cod5 imPlgmentAtion w)th nulry. Does )| work well=
誤り訂正有りの復号結果: I trùed Hamming cod5 implementation with nulpy. Does it work well?
今回のケースについては、誤り発生率0.01までは完璧に訂正できていることが確認できます。
ちなみに誤り発生率 0.02の結果を見ると、誤り訂正無しの復号化では「Hamming」と元の入力通りになっているのに誤り訂正有りの復号化で「Hamminf」と誤った結果になっている部分が存在します。これでは誤り訂正によって逆に誤りを引き起こしているかのように見えます。しかし調べてみるとこれは想定通りの挙動でした。該当部分の誤り訂正無しにおけるハミング符号を見てみると、復号化処理で影響を与えない($R$ で0埋めされている行に対応する)複数のbitにノイズが載っていました。複数のbitにノイズが乗っている時点で誤り訂正は正しく機能しませんが、一方でノイズの乗り方が復号化処理に影響を与えないものであったため、このような事象が見られたわけです。
誤り訂正が可能となる確率について
実装の説明の中でも触れましたが、ハミング符号は各行に高々誤りが1ヵ所という前提の下で誤り訂正が可能です。各bitでの誤り発生確率が $p$ で互いに独立だとすると、(7,4)ハミング符号において、各行で誤り訂正が機能して元の情報が得られる確率は
$$ (1 - p)^{7} + 7p(1 - p)^{6} $$
となります(1ヵ所も誤りがない確率+1ヵ所誤りが起きる確率)。
実装例の中で試していた $p$ に対してこの確率を計算してみると下記のようになります。ちょっとした短文であっても、各行99%程度の訂正成功率では訂正ミスが紛れ込むものなのだなとわかります。
f = lambda p: (1 - p) ** 7 + 7 * p * ((1 - p) ** 6)
for p in [0.01, 0.02, 0.03, 0.04, 0.05]:
print(f(p))
# -> 0.9979689583650599
# 0.9921434665676799
# 0.9829069658162197
# 0.9706196592230398
# 0.9556194578124997
本記事のまとめ
- ハミング符号をnumpyで実装してみました
- 誤り訂正が成功する確率を確認してみました
参考文献
以上、Classi Advent Calendar 2020 の2日目の記事でした。
明日の担当は @kozy4324 さんです。楽しみですね。