二分法で遊んでいると、二分法で三重行列の固有値が計算できると知り、これは面白いと思いまとめてみました。この方法はランチョス法と組み合わせて、大規模疎行列の固有値問題を解くときに使うようです。
三重対角行列
三重対角行列行列というのは以下のように対角成分とその両脇のみ非ゼロの値を持つ行列のことです。
M = \begin{pmatrix}
a_1 & b_1 & 0 & \cdots & 0 \\
b_1 & a_2 & b_2 & \cdots & 0 \\
0 & b_2 & a_3 & \cdots & 0\\
\vdots & \vdots & \ddots & & \vdots \\
0 & \cdots & b_{n-2} & a_{n-1} & b_{n-1}\\
0 & \cdots & 0 & b_{n-1} & a_{n}
\end{pmatrix}
一般に三重対角行列の非対角成分は必ずしも対称とは限りませんが、ここでは対称な場合に限って扱います。
すると、この行列式は
p_n(\lambda) = \begin{vmatrix}
\lambda - a_1 & -b_1 & 0 & \cdots & 0 \\
- b_1 & \lambda - a_2 & -b_2 & \cdots & 0 \\
0 & -b_2 & \lambda - a_3 & \cdots & 0\\
\vdots & \vdots & \ddots & & \vdots \\
0 & \cdots & -b_{n-2} & \lambda - a_{n-1} & -b_{n-1}\\
0 & \cdots & 0 & -b_{n-1} & \lambda - a_{n}
\end{vmatrix}
と書けるので、多項式$p_k$について以下の漸化式が成り立ちます。
\left\{
\begin{array}{ll}
p_0 = 1 & \\
p_1 = \lambda - a_1 & \\
p_k = (\lambda - a_k)p_{k-1} - b^2_{k-1}p_{k-2} & (k\geq 2)
\end{array}
\right.
便宜上、$p_0=1$としています。
スツルムの方法
実はこの多項式列$p_k$はスツルム列というものになっています。
スツルム列
関数列$f_0(x),f_1(x),\cdots,f_n(x)$がある区間$[a,b]$で以下の4つを満たすとき、$(f_k)_{k=0}^n $は区間$[a,b]$においてスツルム列をなすという:
(1) $f_0=const.\neq0$
(2) $f_k$と$f_{k-1}$の根($f_k=0$としたときの解)が異なる
(3) $\forall x_0$ s.t. $f_k(x_0)=0 \Rightarrow f_{k+1}(x_0)f_{k-1}(x_0)<0$
(4) $\forall x_0$ s.t. $f_n(x_0)=0 \Rightarrow \frac{df_{n}}{dx}(x_0)f_{n-1}(x_0)>0$
そして、以下のスツルムの定理が成り立ちます。
スツルムの定理
実係数多項式列$(f_k(x))^n_{k=0}$が区間$[a,b]$でスツルム列であり、$f_n(a)f_n(b)\neq0$であるとする。このとき、$ x \in [a,b]$に対して$f_n(x),f_{n-1}(x),f_{n-2}(x),\cdots,f_1(x),f_0(x)$
を左から順にみていき、その符号変化の回数を$N(x)$とすれば、$x\in[a,b]$における$f_n(x)=0$の解の個数は$n(b:a)=N(b)-N(a)$個である。
$N(x)$の計算では、$f_k$と$f_{k-1}$の符号が同じかどうかを見ていきます。
ややこしいので、まずは$n=3$として4つ例を見てみます。ある$x$に対して、
- $f_0=1,f_1=2,f_2=-1,f_3=5$のとき、$N(x)=2$です。
- $f_0=1,f_1=2,f_2=0,f_3=5$のとき、$N(x)=0$です。(正->0->正は符号変化なしです)
- $f_0=1,f_1=-1,f_2=0,f_3=-5$のとき、$N(x)=1$です。(負->0->負は符号変化なしです)
- $f_0=1,f_1=0,f_2=-2,f_3=-3$のとき、$N(x)=1$です。(正->0->負は符号変化があります)
以上のようになります。$0$を含む場合の取り扱いに注意しましょう。
そこで、このスツルムの定理を利用して$p_n(\lambda)=0$の解、つまり固有値を計算します。固有値$(\lambda_k)$を
a<\lambda_1 < \lambda_2 < \cdots <\lambda_n<b
とおきます。簡単のために固有値の縮退は無いものとします。
ここで、$[a',b'] \subset [a,b]$のとき、$(f_k)$は区間$[a',b']$においてもスツルム列であり、しかも区間が狭くなっています。このとき$ n(b':a') \leq n(b:a)$となり、区間を狭めていくと、ちょうど固有値の値が区間の外に出たときに、$n(b:a)$が小さくなることが分かります。よって、
a<\lambda_{k-1}<b'<\lambda_k<b<\lambda_{k+1}
のとき、$n(b:a)= k$、$n(b':a)=k-1$となります。この$b$を二分法で狭めていって$k$番目に大きい固有値が求まります。
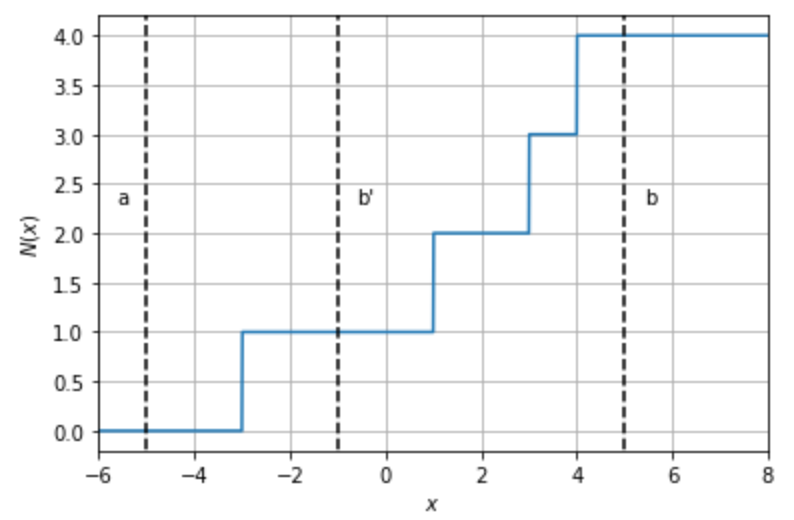
例えば、次図は固有値が$[-1,1,3,4]$となる$4\times4$の三重対角行列の場合における$N(x)$のグラフです。$N(a)=0$なので、$n(b:a)=N(b)$となります。例えば、3番目に大きい固有値を求めたいときは
\begin{align}
b_{piv} &= \frac{b+b'}{2}\\
N(b_{piv}) &>2 \Rightarrow b \leftarrow b_{piv} \\
N(b_{piv}) &<2 \Rightarrow b' \leftarrow b_{piv}
\end{align}
と更新します。すると、最終的には$b,b'\simeq 1$となります。
初期値の設定
では、さっそく実装を...と行きたいところですが、二分探索の初期値$a,b$は、$\forall \lambda_k \in [a,b]$となるようにとらなければいけません。これを与えてくれるのゲルシュゴリンの定理です。
ゲルシュゴリンの定理
行列
A=\begin{pmatrix}
a_{11} & \cdots & a_{1n} \\
\vdots & \ddots & \ \vdots \\
a_{n1} & \cdots & a_{nn}
\end{pmatrix}
に対して、
R_i = \sum_{j\neq i}|a_{ij}| \quad (iは固定)
とし、中心$a_{ii}$、半径$R_i$の円板$D_i=D(a_{ii},R_i)$をゲルシュゴリン円板と定義する。
このとき、$A$の任意の固有値$\lambda$に対して、あるゲルシュゴリン円板$D_i$が存在して、
\lambda \in D_i \Leftrightarrow |\lambda - a_{ii}| \leq R_i.
このことから、
\begin{align}
L &= \min[a_k - (|b_{k-1}|+|b_k|)] \\
R &= \max[a_k + (|b_{k-1}|+|b_k|)]
\end{align}
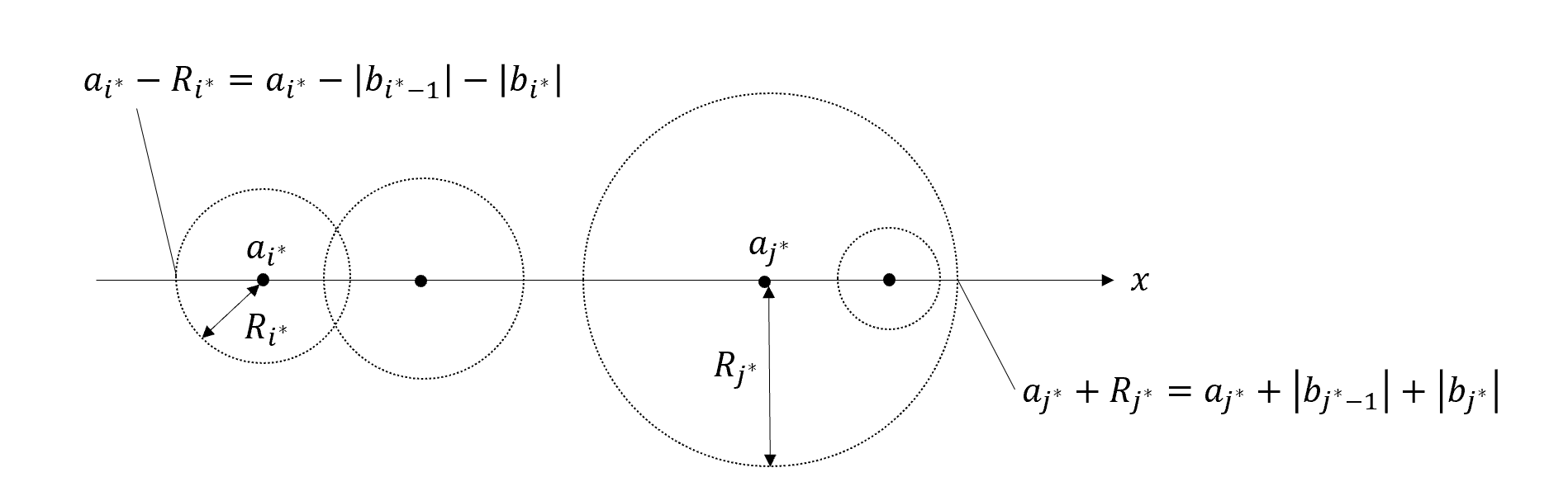
とすると三重対角行列$M$の任意の固有値は$\lambda \in [L,R]$となることが言えます。下図のような数直線を考えると、各円(=ゲルシュゴリン円板)の中にそれぞれ固有値が1個ずつ存在するからです。
この$L,R$を二分探索の初期値とします。
図中の記号については
\begin{align}
i^* &= \mathrm{argmin}[a_k - R_k] \\
j^* &= \mathrm{argmax}[a_k + R_k]
\end{align}
です。
実装
以上の内容をpython3で実装してみましょう。
numpyをインストールしておきます。
import numpy as np
import numpy.linalg as LA
まず、サイズ$n$の行列の対角成分と非対角成分の列$a,b$を乱数で適当に生成します。
n=10
a = np.random.randint(1,n,n)
b = np.random.randint(1,n,n-1)
次にスツルムの方法で固有値を求めるクラスを作ります。
class Strum():
def __init__(self,th):
#実数の探索なので閾値を決める
self.th = th
#スツルム列の符号の変化回数を数える
def sign_flip(self,x:float,n:int, a:list, b:list):
cnt = 0
p0 = 1
p1 = x-a[0]
for i in range(0,n-1):
#小行列式の漸化式
p2 = (x-a[i+1])*p1 - b[i]*b[i]*p0
if( p0*p1<0 ): cnt += 1
#正->0->負/負->0->正だった場合
elif( abs(p1)<th and p0*p2<0 ): cnt += 1
if( i<n-2 ):
p0=p1
p1=p2
#最後の端の部分
if( p1*p2<0 ): cnt += 1
return cnt
def bis(self,n:int,a:list,b:list):
#固有値の範囲を求める (Gershgorin)
lim0 = np.infty
lim1 = -np.infty
for i in range(0,n-2):
lim0 = min(lim0,a[i+1]-(b[i]+b[i+1]))
lim1 = max(lim1,a[i+1]+(b[i]+b[i+1]))
eig_arr = np.array([lim1])
#i番目に大きい固有値を二分探索で大きい順に求める
#上限の値はi-1番目に大きい固有値を使えばよい
for i in range(n):
x0 = lim0
x1 = eig_arr[0]
while(x1-x0>self.th):
piv = (x0+x1)/2
w = self.sign_flip(piv,n,a,b)
if( w<=i ): x1 = piv
else: x0 = piv
eig_arr = np.append(eig_arr,x1)
return eig_arr[1:]
これを使って、
#閾値
th=1e-6
strum = Strum(th)
#降順に出力されるので、昇順に直す
eig2 = strum.bis(n,a,b)[::-1]
で固有値を求めます。
一方、普通に対角化して求めるために、次の関数で列$a,b$から三重対角行列をつくります。
#3重対角行列の生成
def tridiag(n,a,b):
mat = np.diag(a)
for i in range(n-1):
mat[i][i+1]=b[i]
mat[i+1][i]=b[i]
return mat
それを
eig1 = LA.eigvalsh(tridiag(n,a,b))
で対角化して、固有値をスツルムの方法で求めた場合と比較してみましょう。
では、実際に$n=8$で回してみます。生成された行列は
array([[6, 1, 0, 0, 0, 0, 0, 0],
[1, 7, 6, 0, 0, 0, 0, 0],
[0, 6, 1, 2, 0, 0, 0, 0],
[0, 0, 2, 3, 1, 0, 0, 0],
[0, 0, 0, 1, 3, 6, 0, 0],
[0, 0, 0, 0, 6, 4, 7, 0],
[0, 0, 0, 0, 0, 7, 3, 1],
[0, 0, 0, 0, 0, 0, 1, 4]])
です。
eig1、eig2の答えは
array([-5.79298523, -3.2100979 , 2.26256171, 3.61443155, 4.43374938,
5.9135213 , 10.99238561, 12.78643357]),
array([-5.7929846 , -3.21009755, 2.26256233, 3.6144318 , 4.43374979,
5.91352159, 10.9923858 , 12.78643399])
となって、ちゃんと閾値の範囲の誤差で一意しています。
参考ページ
- http://www.st.nanzan-u.ac.jp/info/gr-thesis/ms/2004/torii/01mm089.pdf
- https://www.math.nagoya-u.ac.jp/~naito/lecture/2010_SS/ex14.pdf
- https://ja.wikipedia.org/wiki/%E3%82%B9%E3%83%84%E3%83%AB%E3%83%A0%E3%81%AE%E5%AE%9A%E7%90%86
- https://ja.wikipedia.org/wiki/%E3%82%B2%E3%83%AB%E3%82%B7%E3%83%A5%E3%82%B4%E3%83%AA%E3%83%B3%E3%81%AE%E5%AE%9A%E7%90%86