物性物理学ではしばしは材料のに応答特性をイメージするためにフェルミ面の図が必要とされることがあります。
そこでFermisurferというソフトを使ってこのようなプロットを行う方法をご紹介します。
今回は第一原理計算の結果から得たFermi面をプロットしたいと思います。
例として$Bi_2Se_3$という物質の計算結果を用いたいと思います。この材料の第一原理計算はこちらの記事をご覧ください。
これにはDOS計算(成分分解しないもの)の下処理の計算を行う必要があるので、まずはQuantum espressoでのDOS計算の仕方をお伝えしたいと思います。
Quantum Espressoでの計算
DOSの計算の入力
次の入力ファイルを用意します。
でのバンド計算の下準備の計算とほとんど同じです。
k点メッシュを$8\times8\times8$にしましたが、フェルミ面を書くにはかなり制度が必要なので、もっと細かく取る必要があるかもしれません。
&CONTROL
calculation = 'bands' ,
wf_collect = .true. ,
outdir = './output' ,
pseudo_dir = '~/q-e-qe-6.5/pseudo/' ,
prefix = 'Bi2Se3' ,
disk_io = 'low',
verbosity = 'high' ,
tstress = .true. ,
tprnfor = .true. ,
max_seconds = 170000,
restart_mode = from_scratch,
/
&SYSTEM
ibrav = 0,
celldm(1) = 7.81213,
nat = 5,
ntyp = 2,
ecutwfc = 150 ,
ecutrho = 1500 ,
occupations = 'smearing' ,
degauss = 0.00001 ,
noncolin = .true. ,
lspinorb = .true. ,
nbnd = 240
/
&ELECTRONS
electron_maxstep = 10000000,
conv_thr = 0.0000000001 ,
mixing_beta = 0.5 ,
/
CELL_PARAMETERS {alat}
0.577350269189626 0.000000000000000 2.306079664570230
-0.288675134594813 0.500000000000000 2.306079664570230
-0.288675134594813 -0.500000000000000 2.306079664570230
ATOMIC_SPECIES
Bi 208.98000 Bi.rel-pbe-dn-kjpaw_psl.1.0.0.UPF
Se 78.96000 Se.pbe-dn-kjpaw_psl.1.0.0.UPF
ATOMIC_POSITIONS {crystal}
Bi 0.400460000000000 0.400460000000000 0.400460000000000
Bi 0.599540000000000 0.599540000000000 0.599540000000000
Se 0.209700000000000 0.209700000000000 0.209700000000000
Se 0.790300000000000 0.790300000000000 0.790300000000000
Se 0.000000000000000 0.000000000000000 0.000000000000000
K_POINTS automatic
8 8 8 0 0 0
次にDOS計算の入力ファイルです。
&DOS
outdir = './output',
prefix = 'Bi2Se3',
fildos = 'Bi2Se3.dos',
/
フェルミ面計算のための入力
フェルミ面計算の入力は次のようになります。
&fermi
outdir = './output',
prefix = 'Bi2Se3',
/
実行
これらを次のコマンドで実行します。
../bin/pw.x <Bi2Se3.nscf.dos.in >Bi2Se3.nscf.dos.out
../bin/dos.x <Bi2Se3.dos.in >Bi2Se3.dos.out
../bin/fs.x <Bi2Se3.fs.in >Bi2Se3.fs.out
2つ目のコマンドが終了したらBi2Se3.dosというファイルが生成されます。ここにDOSのデータが入っています。
# E (eV) dos(E) Int dos(E) EFermi = 4.367 eV
-38.638 0.6845E-01 0.6845E-03
-38.628 0.1377E-80 0.6845E-03
-38.618 0.1377E-80 0.6845E-03
-38.608 0.1377E-80 0.6845E-03
-38.598 0.1377E-80 0.6845E-03
-38.588 0.1377E-80 0.6845E-03
-38.578 0.1377E-80 0.6845E-03
-38.568 0.1377E-80 0.6845E-03
-38.558 0.1377E-80 0.6845E-03
-38.548 0.1377E-80 0.6845E-03
-38.538 0.1377E-80 0.6845E-03
-38.528 0.1377E-80 0.6845E-03
-38.518 0.1377E-80 0.6845E-03
-38.508 0.1377E-80 0.6845E-03
-38.498 0.1377E-80 0.6845E-03
-38.488 0.7043E-66 0.6845E-03
-38.478 0.1377E-80 0.6845E-03
-38.468 0.1377E-80 0.6845E-03
:
:
:
また、3つ目のコマンドが終了すると、Bi2Se3_fs.bxsfというファイルが出力されます。これがフェルミ面のデータになっています。このデータをFermiSurferで読み込んでFermi面を描画したいと思います。
FermiSurferによるFermi面の描画
次にFermiSurferを使って得られたFermi面のデータを実際に出力してみます。
インストール
公式ページは
です。また以下のページからダウンロードします。
描画
以下、Windows環境で考えます。FermiSurfer.exeをダウンロードします。ただ、これ単独では実行することはできません。Bi2Se3_fs.bxsfをプログラムから開くなどからFermiSurfer.exeで開きます。
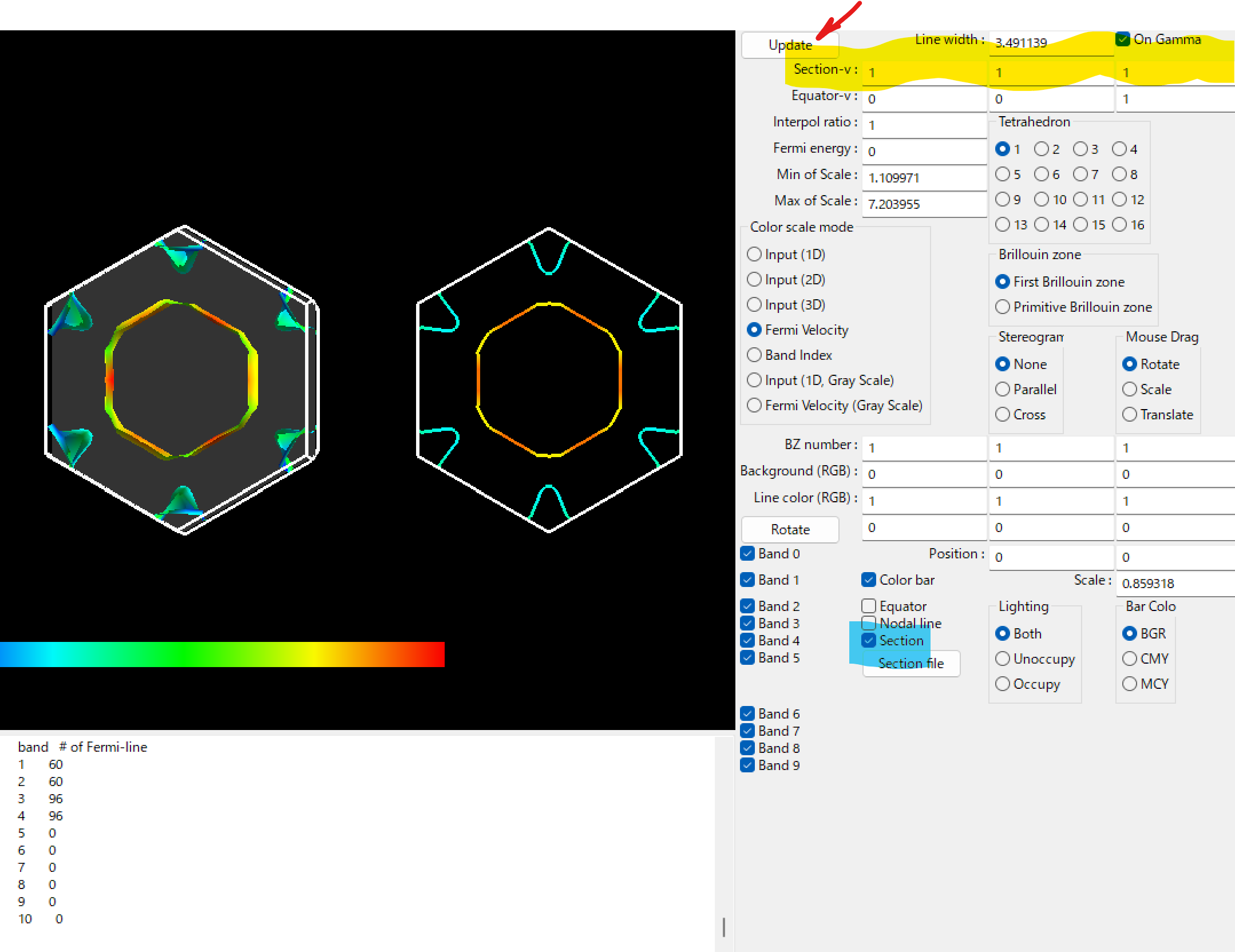
すると、次のような図を得ることができます。図はマウスのドラッグやRotateテキストボックスで回転させることができます。
断面
任意の方向で断面を描くこともできます。
まず、section-v(黄色の網掛け)で断面の法線の係数(基底は逆格子ベクトル)を入力します。
次にsectionボックス(青色の網掛け)にチェックを入れます。そしてupdate(赤矢印)をクリックすると、上図のように断面を出力できます。この図は$(1,1,1)$方向の図です。
また、sectionボックスの下のSection fileというボタンをクリックすると、断面のデータ(fermi_line.dat:フェルミ面の断面のデータとbz_line.dat:ブリリュアンゾーンの断面の頂点のデータ)が出力されます。
タイトバインディング模型から求める場合
次のコードでfrmsfファイルを作成してFermiSurferで出力しても、フェルミ面を描画することができます。これは
でWannier90を使って求めたタイトバインディング模型で第1ブリリュアンゾーンのエネルギーバンドを求めてそのデータを使っています。ただ、計算にはかなり時間がかかるので気を付けてください。
import numpy as np
import scipy.linalg as LA
import pandas as pd
import time
# system size
Lx=8
Ly=8
Lz=8
# band index number
nbnd = 94
# input parameters
output_file = "BiSe3.frmsf"
hr_file = "Bi2Se3_hr.dat"
n_skip = 40
n_band_id = 30
fermi = 8.7764
bravais = np.array([ [ 0.577350269189626, 0.000000000000000, 2.306079664570230],
[-0.288675134594813, 0.500000000000000, 2.306079664570230,],
[-0.288675134594813, -0.500000000000000, 2.306079664570230 ] ])
# %%
from joblib import Parallel, delayed
def parallel( iteration, Njob, Nver, func ):
return Parallel(n_jobs=Njob,verbose=Nver)( [delayed(func)(i) for i in iteration ] )
# %%
def reciprocal( bravais_T ):
reciprocal = np.zeros((3,3))
deno = LA.det( bravais_T.T )
for i in [0,1,2]:
reciprocal[i] = np.cross( bravais_T[(i+1)%3], bravais_T[(i+2)%3] )/deno
return reciprocal
# %%
def hr_file_to_df_hop_with_band_index( hr_file, n_skip ):
col_name_list = ["a1","a2","a3","n_band1","n_band2","hop_real","hop_imag"]
col_dict = {"a1":int,"a2":int,"a3":int,"n_band1":int,"n_band2":int,"hop_real":float,"hop_imag":float}
df_hop = pd.read_table(hr_file, skiprows=[ i for i in range(0,n_skip)], header=None,
sep="\s+", names= col_name_list, dtype=col_dict)
df_hop["hop"] = df_hop["hop_real"] + 1j*df_hop["hop_imag"]
df_hop["n_band1"] -= 1; df_hop["n_band2"] -= 1
return df_hop.drop( ["hop_real","hop_imag"], axis=1 )
def make_hamiltonian_list( k_arr, df_hop, size, fermi, threshold=1e-4 ):
hami_list = [ np.zeros((size,size),dtype=np.complex128) for i in range( len(k_arr) ) ]
E0 = fermi*np.identity(size)
for sr in df_hop[ abs(df_hop["hop"])>threshold ].itertuples():
an = np.array([ sr.a1, sr.a2, sr.a3 ])
t = sr.hop
row = sr.n_band1
col = sr.n_band2
for i, k in enumerate( k_arr ):
phase = 2*np.pi*np.dot(an,k)
hami_list[i][row,col] += t*( np.cos(phase) + 1j*np.sin(phase) )
return [ h - E0 for h in hami_list ]
def calc_band( Lx, Ly, Lz, df_hop, size, fermi ):
start = time.time()
n_arr = np.array([ [i1,i2,i3] for i1 in range(Lx) for i2 in range(Ly) for i3 in range(Lz)])
k_arr = np.array([ [n[0]/Lx,n[1]/Ly,n[2]/Lz] for n in n_arr ])
hami_list = make_hamiltonian_list( k_arr, df_hop, size, fermi )
band_list = Parallel(n_jobs=-2,verbose=4)( [delayed(LA.eigvalsh)(h) for h in hami_list ] )
band_list = [ Ek.tolist() for Ek in band_list ]
end = time.time()
print( "{0} sec.".format( end - start ) )
df = pd.DataFrame(columns=['x','y','z','n','Energy'])
df_band = pd.DataFrame(n_arr,columns=['x','y','z']).join(pd.DataFrame(band_list))
for i in range(size):
df0 = df_band.loc[:,['x','y','z',i]].rename(columns={i:'Energy'})
df0['n'] = [ i for j in range(Lx*Ly*Lz) ]
df = df.append(df0)
return df
# %%
df_hop = hr_file_to_df_hop_with_band_index( hr_file, n_skip )
# %%
df_band = calc_band(Lx, Ly, Lz, df_hop, n_band_id, fermi)
# %%
df_band = df_band.sort_values(['n','x','y','z'])
recip = reciprocal( bravais ).round(6)
# %%
with open(output_file, 'w') as f_handle:
f_handle.write(str(Lx)+" "+str(Ly)+" "+str(Lz)+"\n")
f_handle.write("1\n")
f_handle.write(str(nbnd)+"\n")
np.savetxt(f_handle, recip, delimiter=' ', fmt ='%.6f')
np.savetxt(f_handle, df_band["Energy"].values, delimiter=' ', fmt ='%.6f')