Nesterovの加速勾配法とは
数値最適化における反復法はある関数$f:\mathbb{R}^m \rightarrow \mathbb{R}^n$に対して、適当な探索方向$d_k$を定義して
x_k \rightarrow x_k + d_k
と更新する方法です。ただし、$d_k$は降下方向でなければならないので、
\lim_{ c \rightarrow 0 } \frac{ f(x_k+cd_k) - f(x_k) }{c} = \nabla f^T(x_k) \cdot d_k < 0
を満たす必要があります。一番簡単なのは$d_k = -\nabla f(x_k)$とする最急降下法です。
しかし、このままでは収束性があまりよくありません。そこでこの収束性をよくする手法の1つがNesterovの加速勾配法です。更新の手順は次のようになります。
x_0 = y_0 \\
x_{k+1} = y_k - \alpha_kf(y_k)\\
y_{k+1} = x_{k+1} + \beta_k (x_{k+1} x_k) \\
(k=0,1,2,\cdots)
パラメーター$\alpha_k$,$\beta_k$のとり方の1例として
\alpha_k = const. = \frac{1}{L} \\
\beta = \frac{k}{k+3}
があります($L$はステップ数)。
実装
Nesterovの加速勾配法で最適化を行うクラスをつくりました。引数には目的関数とその微分を与えます。例として
f(x) = |b - Ax|^2
を目的関数としました。
b = A(1,1,\cdots,1)^T
としたので、$w = (1,1,\cdots,1)^T$で$f$が最小となります。
import numpy as np
from numpy import linalg as LA
from functools import partial
def f(w,A,b):
v1 = b-A@w
return v1.dot(v1)
def df(w,A,b):
AA = (A.T).dot(A)
return -2*A.T@b + 2*AA@w
class NesterovAccelaratedGradient:
def __init__(self,df,threshold):
self.df = df
self.threshold = threshold
def optim(self,w_ini,steps):
#initial guess
w = w_ini
v= w.copy()
err_list = []
for i in range(steps):
dv = self.df(v)
err = LA.norm(dv)
wn = v - 1/steps*dv
err_list.append(err)
if err<self.threshold:
return wn,err_list
v = wn + i/(i+3)*(wn-w)
w=wn.copy()
print("not converged")
return wn,err_list
# m<n
m = 3
n = 5
A = np.array([[0.59, 0.99, 0.81, 0.56, 0.75],
[0.62, 0.56, 0.96, 0.9 , 0.97],
[0.91, 0.03, 0.46, 0.58, 0.21]])
b = A@np.ones(n)
steps=100000
threshold = 1e-3
w_ini = np.ones(n) + 0.01*np.random.random(n)
NAG = NesterovAccelaratedGradient(partial(df,A=A,b=b),threshold)
w_opt,err_list_NAG = NAG.optim(w_ini,steps)
from matplotlib import pyplot as plt
plt.plot(err_list0_NAG)
plt.yscale("log")
plt.legend()
plt.xlabel("iteration")
plt.ylabel("error")
plt.savefig("NAG.pdf")
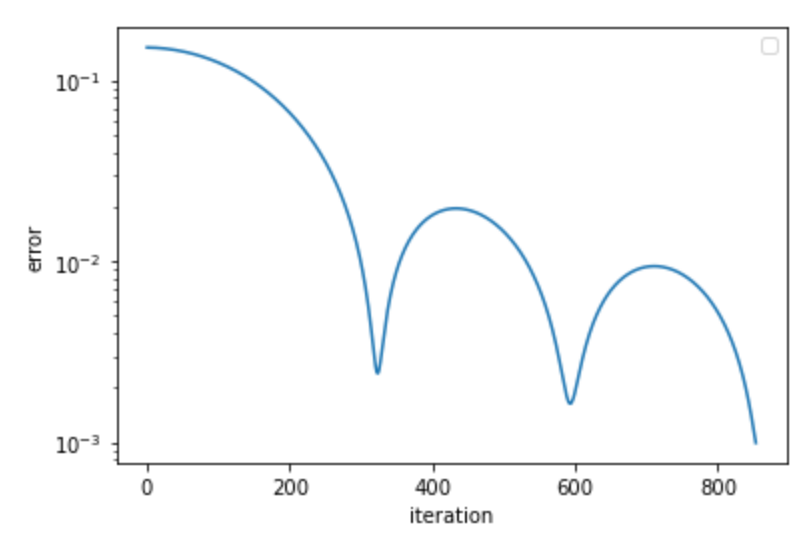
実行結果を見てみます。誤差$|\nabla f|$の反復回数に対する変化をプロットすると、最適化の過程は次のようになっています。
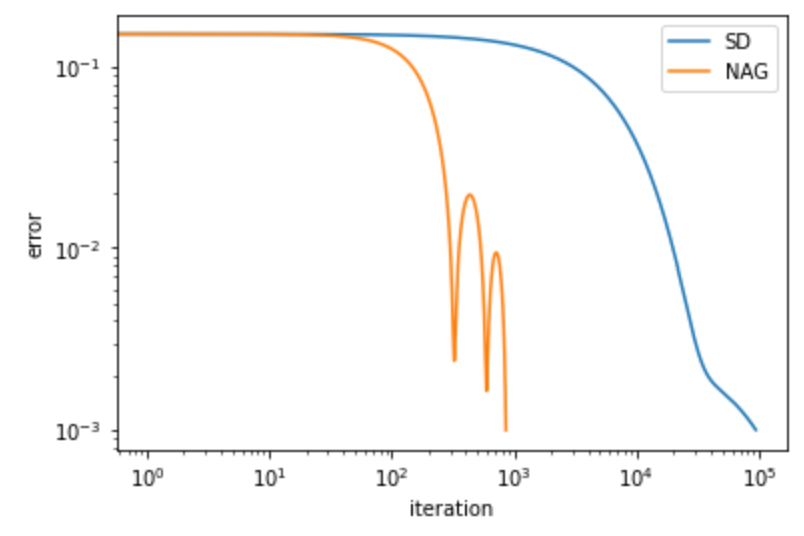
最急降下法(SD)とNesterovの加速勾配法(NAG)の収束性をを比べると次のようになり、確かに改善しています(両軸ともlogスケール)。
また、最終的なoptimalなパラメーターは
w_{opt} = (1.00133097, 0.99971504, 0.99921629, 0.99674919, 1.00312895)
となっていて、確かに$(1,1,\cdots,1)$に近い値になっています。停止条件が$|\nabla f | <10^{-3}$なので、誤差はこのくらいで妥当でしょう。