最近、量子コンピューターがホットトピックだと思います。マシンの性能はまだまだ道のりが長いですが、実用的なアルゴリズムは色々と開発されてます。今回はその中でも個人的に興味を持った組み合わせ最適化についてTPSを例にやってみたいと思います。
量子コンピューター
量子コンピューターとは適切な量子状態$|\Psi\rangle$を恣意的にユニタリ変換することで別の状態$|\Psi'\rangle$へと変化させることで計算を行うシステムのことです。(例えば電磁波を一定時間当てるなどの操作でユニタリ変換を行います。)これは量子ビットと呼ばれる要素で構成されていて、これらが互いに干渉して動いています。$i$番目の量子ビットは単独では状態$s_i=0,1$をとり、$N$量子ビットからなるシステム全体では
|\Psi\rangle = \sum_{s_1,s_2\cdots s_N} c_{s_1,s_2,\cdots, s_N}|s_1s_2\cdots s_N\rangle\\
= c_{00\cdots 0}|00\cdots 0\rangle + c_{00\cdots 01}|00\cdots 01\rangle + \cdots c_{11\cdots 1}|11\cdots 1\rangle
という何らかの重ね合わせ状態が実現しています。$|\Psi\rangle$はしばしば係数$c_{s_1\cdots s_N}$を並べたベクトルで表されます。このとき計算後の状態は(所望の計算に応じた)適切なユニタリ変換行列を用いて
|\Psi'\rangle = \left( \begin{array}{c}
c'_{00\cdots 0} \\ c'_{00\cdots 01} \\ \vdots \\ c'_{11\cdots 1}
\end{array} \right) = U \left( \begin{array}{c}
c_{00\cdots 0} \\ c_{00\cdots 01} \\ \vdots \\ c_{11\cdots 1}
\end{array} \right)
= U |\Psi\rangle
となります。操作後には各量子ビットの状態を測定します。$p'(s_1\cdots s_N)=|c'_{s_1\cdots s_N}|^2$は測定結果で観測される状態が$|s_1\cdots s_N \rangle$である確率になっているので、$|\Psi\rangle \rightarrow |\Psi'\rangle$の操作と$|\Psi'\rangle$の測定を何度も繰り返すことで統計的に確率分布$p'(s_1\cdots s_N)$が得られます。この$p'(s_1\cdots s_N)$と計算結果が対応づけられています。
量子コンピューティングでやることは適切な$|\Psi\rangle$と$U$を設計することです。
今回はこれを利用して各ステップで最適化関数を計算します。
最適化問題
整数ベクトルの有限集合$D$において$x=(x_1\cdots x_n)\in D$に対する関数
f(x)=x^TAx+Bx
を最小化(あるいは$-f(x)$を最大化)する問題Qを考える。
ここで条件$D$は以下のように書けるとする。
c^T_i x \leq d_i \\
l_i \leq x_i \leq u_i
QUBO
このままでは量子コンピューターに落とし込めないので次のように問題Qを言い換えます。
まず、$x_i \in [l_i,u_i]$を$z_j \in [0,1]$で表すために
x_i=\begin{cases}
-\sum_{j=1}^{u_i-l_i}z_j -u_i & u_i \leq 0 \\
\sum_{j=1}^{u_i}z_j - \sum_{j=1}^{l_i} z_{u_i+j} & l_i<0<u_i \\
\sum_{j=1}^{u_i-l_i}z_j + l_i & l_i \geq 0
\end{cases}
とします。また不等式$c^T x\leq d$は新しい変数$y\geq 0$を用いて
c^T x + y =d
という等式に直します。
制約条件は
\tilde{f}(x,y) = f(x) + \lambda\sum_i(c^T_i x + y_i - d_i)^2
と最適化関数に組み込みます。($\lambda > 0$は適当な定数)
最後に$z=(1-s)/2$として$s=\pm1$に直します。
ハミルトニアン
以上の書き換えを駆使して問題Qは十分な数の$N$量子ビットのシステムにおいて
H(s)=\sum_{i,j} w_{ij}s_i s_j + \sum_i v_i s_i + const. \\
s = (s_1, s_2, \cdots, s_N)
のように書くことができます。$s_i s_j$や$s_i$は$|s_1s_2\cdots s_N\rangle$を基底として行列で表すことができます(いわゆる量子力学におけるハミルトニアン)。そしてこの期待値
E(\Psi) = \langle \Psi |H | \Psi \rangle = \sum_s |c_s|^2 H(s)
を最小化して最適な$|\Psi\rangle$を求めます。
量子最適化
量子コンピューターを使って最適化問題を解く方法を紹介します。
QAOA (Quantum Approximate Optimization Algorithm)
|+\rangle = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle) \\
|\Psi_0\rangle = \bigotimes_{i=1}^{N}|+ \rangle
を初期状態としてユニタリ変換
U_p(\beta,\gamma) = e^{-i\beta_p B}e^{-i\gamma_p H } \cdots e^{-i\beta_1 B}e^{-i\gamma_1 H } \\
B = \sum_i s^x_i
を作用させると状態$|\Psi_p(\beta,\gamma)\rangle = U_p(\beta,\gamma)|\Psi_0\rangle$が得られます。
よって
F_p(\beta,\gamma) = \langle \Psi_p(\beta,\gamma) | H | \Psi_p(\beta,\gamma) \rangle
を最小化します。ここの最適化はグリッドサーチや重点サンプリングを用いて行います。
巡回セールスマン問題 (TSP)
巡回セールスマン問題とは重み付きグラフ$G=(V,E,W)$で上ですべてのノードをちょうど1回通り、コストの総和が最小となる閉路を求める問題です。
ここで
V=\{v_i\} \\
E=\{(v_i,v_j) \} \\
W =\{w_{ij}|(v_i,v_j)\in E\}
はそれぞれ頂点、辺、辺のコストです。ノードは$n$個、エッジは$m$本あるとします。
TSPの最適化関数
ノードを1つずつ順番に移動することを考えます。
現在$i$番目に通るノード$v_{j_1}$にいるとして次の$i+1$番目のステップでは$v_{j_2}$に移るとします。すると$i\rightarrow i+1$番目の移動でかかるコストは$w_{j_1j_2}$です。
そこで、$i$番目にノード$v_j$を通るかどうかを$t_{ij}=0,1$で表すことにすると、
最適化すべき量は
\sum_{j_1j_2}w_{j_1j_2}\sum_{i=0}^{n} t_{ij_1}t_{i+1,j_2}
です。ただし、閉路であることから$i=n$と$i=0$は同一視しています。
次に制約条件を考えます。
各ステップ$i$で同時に複数のノードにいることはありえません。また、各ノードは1度しか通らないので
\forall i, \exists! j, \quad s.t. \quad t_{ij}=1 \\
\forall j, \exists! i, \quad s.t. \quad t_{ij}=1
が成り立ちます。$t_{ij}=0,1$なのでこれらの条件は
\sum_i t_{ij}=1 \\
\sum_j t_{ij}=1
と表されます。
以上から最適化関数は
L(t) = \sum_{j_1j_2}w_{j_1j_2}\sum_{i=0}^{n} t_{ij_1}t_{i+1,j_2} + \lambda\sum_{j=1}^{n}(1-\sum_i t_{ij})^2 + \lambda\sum_{i=0}^{n-1}(1-\sum_j t_{ij})^2
となります。
実装
qiskitを使ってpythonで実装します。コードはIBM-Quantum( https://quantum-computing.ibm.com ) にあるIBMの適当なマシンで流します。
まず使うパッケージです。
import itertools
import networkx as nx
import numpy as np
import matplotlib.pyplot as plt
#%matplotlib inline
import qiskit
from qiskit import QuantumCircuit, Aer, execute, transpile
from qiskit.circuit import ParameterVector
from qiskit.utils import QuantumInstance, algorithm_globals
from qiskit.opflow import I, X, Y, Z, PauliSumOp
from qiskit.algorithms import VQE, QAOA
from qiskit.algorithms.optimizers import COBYLA
from qiskit.circuit.library import TwoLocal
from qiskit_optimization import QuadraticProgram
from qiskit_optimization.algorithms import MinimumEigenOptimizer
from qiskit.optimization.applications.ising import max_cut, tsp
from qiskit.aqua import aqua_globals
from docplex.mp.model import Model
次にIBM-Quantumでコードを実行するために登録したアカウントでログインします。
from qiskit import IBMQ
from qiskit.providers.ibmq import least_busy
from qiskit.providers.aer.noise import NoiseModel
from qiskit.tools.monitor import job_monitor
IBMQ.enable_account('登録アカウントのトークンを入力')
provider = IBMQ.get_provider(hub='ibm-q', group='open', project='main')
次は最適化のパラメーターと出力する図の名前です。
seed = 10598
maxiter = 1000
MAX_COORD = 100
figname_graph = "graph4"
figname_sol = "route4.real"
figname_opt = "opt4.real"
グラフやパスを描画する関数です。
def draw_graph(G, colors, pos, prefix):
fig = plt.figure()
default_axes = plt.axes(frameon=True)
nx.draw_networkx(G, node_color=colors, node_size=600, alpha=.8, ax=default_axes, pos=pos)
edge_labels = nx.get_edge_attributes(G, 'weight')
nx.draw_networkx_edge_labels(G, pos=pos, edge_labels=edge_labels)
fig.savefig(prefix+".pdf")
def draw_tsp_solution(G, order, colors, pos, prefix):
fig = plt.figure()
G2 = nx.DiGraph()
G2.add_nodes_from(G)
n = len(order)
for i in range(n):
j = (i + 1) % n
G2.add_edge(order[i], order[j], weight=G[order[i]][order[j]]['weight'])
default_axes = plt.axes(frameon=True)
nx.draw_networkx(G2, node_color=colors, edge_color='b', node_size=600, alpha=.8, ax=default_axes, pos=pos)
edge_labels = nx.get_edge_attributes(G2, 'weight')
nx.draw_networkx_edge_labels(G2, pos, font_color='b', edge_labels=edge_labels)
fig.savefig(prefix+".pdf")
counts = []
values = []
def store_intermediate_result(eval_count, parameters, mean, std, skip = 20):
if(eval_count%skip==0): print("count: {}, mean: {}, std: {}".format(eval_count,mean,std))
counts.append(eval_count)
values.append(mean)
ではメインパートに入ります。まずはノード数$n$の適当な重み付きグラフを生成します。
n = 4
# position of each node on xy plane
coord = aqua_globals.random.uniform(0, MAX_COORD, (n, 2))
ins = tsp.calc_distance(coord, 'tmp')
print('distance\n', ins.w)
# Draw the graph
G = nx.Graph()
G.add_nodes_from(np.arange(0, ins.dim, 1))
colors = ['r' for node in G.nodes()]
for i in range(0, ins.dim):
for j in range(i+1, ins.dim):
G.add_edge(i, j, weight=ins.w[i,j])
# Generate plot of the Graph
colors = ['r' for node in G.nodes()]
default_axes = plt.axes(frameon=True)
pos = nx.circular_layout(G)
draw_graph(G, colors, pos, figname_graph)
次にDocplexというパッケージを使って対応する最適化関数を作ります。
def model(G,num_node):
mdl = Model(name='tsp')
x = {(i,p): mdl.binary_var(name='x_{0}_{1}'.format(i,p)) for i in range(num_node)
for p in range(num_node)}
# Object function
tsp_func = mdl.sum(ins.w[i,j] * x[(i,p)] * x[(j,(p+1)%num_node)] for i in range(num_node) for j in range(num_node) for p in range(num_node))
# Constraints
for i in range(num_node):
mdl.add_constraint(mdl.sum(x[(i,p)] for p in range(num_node)) == 1)
for p in range(num_node):
mdl.add_constraint(mdl.sum(x[(i,p)] for i in range(num_node)) == 1)
mdl.minimize(tsp_func)
return mdl
mod = model(G,n)
print(mod.export_as_lp_string())
実行のために使うマシン(またはシミュレーター)の情報を読み込みます。(ここでは実機をチョイスしました。コメントアウトした方のインスタンスに切り替えればシミュレーターで疑似的に量子計算をしてくれます。)
# instance for a simulator
algorithm_globals.random_seed = seed
backend = Aer.get_backend('aer_simulator')
ins_simulator = QuantumInstance(backend, seed_simulator=seed, seed_transpiler=seed)
# instance for a real device
backend_filter = lambda b: (not b.configuration().simulator) and b.configuration().n_qubits >= n*n and b.configuration().quantum_volume >= 9 and b.status().operational
backend = least_busy(provider.backends(filters=backend_filter))
print("The best backend is " + backend.name())
noise_model = NoiseModel.from_backend(backend)
#print(noise_model)
algorithm_globals.random_seed = seed
ins_noise = QuantumInstance(backend=Aer.get_backend('aer_simulator'), seed_simulator=seed, seed_transpiler=seed, noise_model=noise_model)
# switch instance
#instance = ins_simulator
instance = ins_noise
counts = []
values = []
qp = QuadraticProgram()
qp.from_docplex(mod)
# solve quadratic program
qaoa = QAOA(optimizer=COBYLA(maxiter=maxiter),callback=store_intermediate_result,
quantum_instance=instance, reps=2)
min_eigen_optimizer = MinimumEigenOptimizer(qaoa)
result = min_eigen_optimizer.solve(qp)
print(result)
print('feasible:', tsp.tsp_feasible(result.x))
QAOAアルゴリズムを実行する関数QAOAをCOBYLAというタイプの最適化手法で計算します。
counts = []
values = []
qp = QuadraticProgram()
qp.from_docplex(mod)
# solve quadratic program
qaoa = QAOA(optimizer=COBYLA(maxiter=maxiter),callback=store_intermediate_result,
quantum_instance=instance, reps=2)
min_eigen_optimizer = MinimumEigenOptimizer(qaoa)
result = min_eigen_optimizer.solve(qp)
print(result)
print('feasible:', tsp.tsp_feasible(result.x))
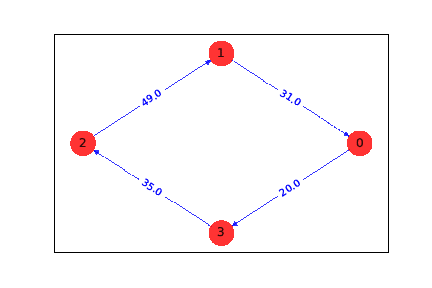
最後に結果を出力します。
if(tsp.tsp_feasible(result.x)):
z = tsp.get_tsp_solution(result.x)
print('solution:', z)
print('solution objective:', tsp.tsp_value(z, ins.w))
draw_tsp_solution(G, z, colors, pos, figname_sol)
plt.plot(counts,values)
plt.xlabel("iteration"); plt.ylabel("energy"); plt.grid()
plt.savefig(figname_opt + ".pdf")
実行結果
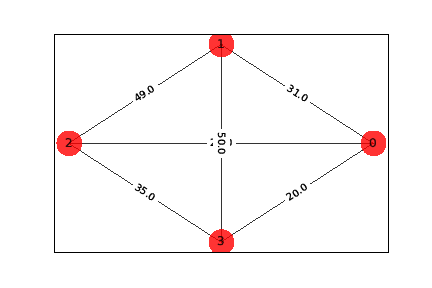
$n=4$で実行してみます。次のグラフで計算します。
$50.0$の数字の裏に隠れている数字は$29.0$です。結果は次のようになります。
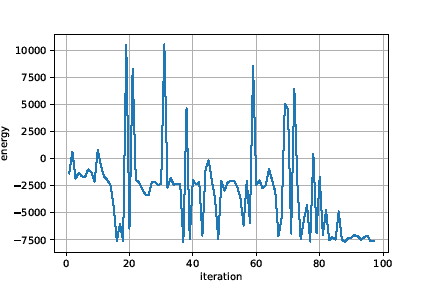
最適化の過程は次図のようになります。
コメント
- $n=4$でも結構計算が重いです。
- $n=5$以上ではおそらくまともな解を得ることができません。これは現在の量子コンピューターのスペックの問題です。現在のマシンではまだ計算を精度良く行うことができないので$n=5$以上の場合では誤差がまだまだ大きいです。
参考ページ
-https://qiskit.org/textbook/ja/ch-applications/qaoa.html
-https://quantum-computing.ibm.com/