ハバード模型の平均場計算で、電子の集団の相転移を計算しよう

物理学で相転移を扱うときは平均場近似をするのが定番だろうが、大学で習うのはおそらくイジング模型の平均場近似だけであろう。しかし実際には電子系のモデルでも平均場近似ができて、単純な相転移に対しては簡単で有効な物理シミュレーションができる。

ここでは簡単のために1/2フィリング(各サイトに電子１個存在することに相当する電子密度)の場合で、1次元ハバードモデルを題材とする。

有効模型

1次元正方格のタイトバインディングモデルは
$\mathbf{a}$を基本並進ベクトルとして、周期$L$の周期的境界条件として

H_0 = t \sum_\mathbf{R} c^\dagger_\sigma(\mathbf{R}) c_\sigma(\mathbf{R+a})

と表される。これはフーリエ変換

c_\sigma(\mathbf{R}) = \frac{1}{\sqrt{L^2}}\sum_\mathbf{k}　c_\sigma(\mathbf{k}) e^{i\mathbf{k}\cdot \mathbf{R} }

を使って

H_0 = 2t \sum_\mathbf{k} \cos{k} c^\dagger_\sigma(\mathbf{k}) c_\sigma(\mathbf{k})

と対角化できる。
しかし、2次元正方格子ハバード模型

\begin{align}
H &= t \sum_\mathbf{R}[ c^\dagger_\sigma(\mathbf{R}) c_\sigma(\mathbf{R+a_1}) +  c^\dagger_\sigma(\mathbf{R}) c_\sigma(\mathbf{R+a_2})] \\
& \qquad + U\sum_\mathbf{R}c^\dagger_\uparrow(\mathbf{R}) c_\uparrow(\mathbf{R}) c^\dagger_\downarrow(\mathbf{R}) c_\downarrow(\mathbf{R}) \\
&= H_0 + H_{int}
\end{align}

は相互作用項$H_{int}$のせいでこれができない。そこでこの部分を平均場近似してフーリエ変換できる１体項にする。

$H_{int}$はハートリー項とフォック項と呼ばれる２つの項に近似できる　この２つは熱力学的平均値に置き換える際の分け方の違いによる。(実はファインマン図を考えると、１次の自己無撞着方程式では２種類(うち一方は３パターン)の項を考えないといけない。)

ハートリー項

まずハートリー項は$c^\dagger_\uparrow(\mathbf{R}) c_\uparrow(\mathbf{R})$と$c^\dagger_\downarrow(\mathbf{R}) c_\downarrow(\mathbf{R})$の２つのペアで考える。

\begin{align}
(ハートリー項) &= U\sum_\mathbf{R}(c^\dagger_\uparrow(\mathbf{R}) c_\uparrow(\mathbf{R}) - \langle c^\dagger_\uparrow(\mathbf{R}) c_\uparrow(\mathbf{R}) \rangle + \langle c^\dagger_\uparrow(\mathbf{R}) c_\uparrow(\mathbf{R}) \rangle )( c^\dagger_\downarrow(\mathbf{R}) c_\downarrow(\mathbf{R}) - \langle c^\dagger_\downarrow(\mathbf{R}) c_\downarrow(\mathbf{R}) \rangle + \langle c^\dagger_\downarrow(\mathbf{R}) c_\downarrow(\mathbf{R}) \rangle ) \\

&= U\sum_\mathbf{R} \left[ \langle c^\dagger_\downarrow(\mathbf{R}) c_\downarrow(\mathbf{R}) \rangle c^\dagger_\uparrow(\mathbf{R}) c_\uparrow(\mathbf{R}) + \langle c^\dagger_\uparrow(\mathbf{R}) c_\uparrow(\mathbf{R}) \rangle c^\dagger_\downarrow(\mathbf{R}) c_\downarrow(\mathbf{R}) -  \langle c^\dagger_\uparrow(\mathbf{R}) c_\uparrow(\mathbf{R}) \rangle\langle c^\dagger_\downarrow(\mathbf{R}) c_\downarrow(\mathbf{R}) \rangle + (c^\dagger_\uparrow(\mathbf{R}) c_\uparrow(\mathbf{R}) - \langle c^\dagger_\uparrow(\mathbf{R}) c_\uparrow(\mathbf{R}) \rangle)(c^\dagger_\downarrow(\mathbf{R}) c_\downarrow(\mathbf{R}) - \langle c^\dagger_\downarrow(\mathbf{R}) c_\downarrow(\mathbf{R}) \rangle) \right]
\end{align} 

$c^\dagger c - \langle c^\dagger c \rangle$の部分が微小だと仮定して、

(ハートリー項) \simeq U\sum_\mathbf{R} \left[ \langle c^\dagger_\downarrow c_\downarrow \rangle c^\dagger_\uparrow(\mathbf{R}) c_\uparrow(\mathbf{R}) + \langle c^\dagger_\uparrow c_\uparrow \rangle c^\dagger_\downarrow(\mathbf{R}) c_\downarrow(\mathbf{R}) - \langle c^\dagger_\uparrow c_\uparrow \rangle\langle c^\dagger_\downarrow( c_\downarrow \rangle \right]

フォック項

フォック項は

H_{int} = -U\sum_\mathbf{R}c^\dagger_\uparrow(\mathbf{R}) c_\downarrow(\mathbf{R}) c^\dagger_\downarrow(\mathbf{R})c_\uparrow(\mathbf{R}) 

と順番を入れ替えて(符号に注意)、$c^\dagger_\uparrow(\mathbf{R}) c_\downarrow(\mathbf{R}) $と$c^\dagger_\downarrow(\mathbf{R})c_\uparrow(\mathbf{R}) $をペアにして考える。

(フォック項) \simeq -U\sum_\mathbf{R}[ \langle c^\dagger_\downarrow c_\uparrow \rangle c^\dagger_\uparrow(\mathbf{R}) c_\downarrow(\mathbf{R}) + \langle c^\dagger_\uparrow c_\downarrow \rangle c^\dagger_\downarrow(\mathbf{R}) c_\uparrow(\mathbf{R}) -  \langle c^\dagger_\uparrow c_\downarrow \rangle\langle c^\dagger_\uparrow c_\downarrow \rangle]

すると、$H_{int}$は次のようにあらわされる

H_{int} \simeq H_{int}^{eff} = \sum_\mathbf{R} \mathbf{c}^\dagger(\mathbf{R}) \begin{pmatrix}
 U\langle c^\dagger_\downarrow c_\downarrow \rangle & -U\langle c^\dagger_\downarrow c_\uparrow \rangle \\
-U\langle c^\dagger_\uparrow c_\downarrow \rangle & U\langle c^\dagger_\uparrow c_\uparrow \rangle
\end{pmatrix} \mathbf{c}(\mathbf{R}) + const.

ここで、平均場の引数$\mathbf{R}$をなくしたが、実はこの平均場は$\mathbf{R}$に依存しない量になっている。理由は後述する。
また、電荷密度$n$とスピン$m_i$($i=x,y,z$)の熱力学的平均値は

\begin{align}
m_i &= \langle \mathbf{c}^\dagger \sigma_i \mathbf{c} \rangle \\
n &= \langle \mathbf{c}^\dagger I \mathbf{c} \rangle
\end{align}

だから

\begin{align}
m_x &= \langle c^\dagger_\uparrow c_\downarrow \rangle + \langle c^\dagger_\downarrow c_\uparrow \rangle \\
m_y &= -i\langle c^\dagger_\uparrow c_\downarrow \rangle + i\langle c^\dagger_\downarrow c_\uparrow \rangle \\
m_z &= \langle c^\dagger_\uparrow c_\uparrow \rangle - \langle c^\dagger_\downarrow c_\downarrow \rangle \\
n &= \langle c^\dagger_\uparrow c_\uparrow \rangle + \langle c^\dagger_\downarrow c_\downarrow \rangle
\end{align}

と書けて、

\begin{align}
 H_{int}^{eff} &= -\frac{U}{2}\sum_\mathbf{R} \mathbf{c}^\dagger(\mathbf{R}) \begin{pmatrix}
m_z - n & m_x-im_y \\
m_x + im_y & -m_z-n
\end{pmatrix}  \mathbf{c}(\mathbf{R}) \\
 &= -\frac{U}{2}\sum_\mathbf{k} \mathbf{c}^\dagger(\mathbf{k}) \begin{pmatrix}
m_z - n & m_x-im_y \\
m_x + im_y & -m_z-n
\end{pmatrix}  \mathbf{c}(\mathbf{k})
\end{align}

となる(定数項は化学ポテンシャルの変化として加味するので、ここでは省略する)。

よって平均場近似した有効模型は

\begin{align}
H_{eff} &= H_0 + H_{int}^{eff} \\
&= \sum_\mathbf{k} \mathbf{c}^\dagger(\mathbf{k}) \begin{pmatrix}
2t\cos{k}-\frac{U}{2}(m_z - n) & -\frac{U}{2}(m_x-im_y) \\
-\frac{U}{2}(m_x + im_y) & 2t\cos{k}-\frac{U}{2}(-m_z-n)
\end{pmatrix}  \mathbf{c}(\mathbf{k}) + const.\\
&= \sum_{\mathbf{k},\sigma,\sigma'} h^{eff}_{\sigma,\sigma'} c^\dagger_\sigma c _{\sigma'}  + const.
\end{align}

これを対角化して固有値、固有ベクトルのユニタリ行列は

\begin{align}
E(\mathbf{k}) &= 2t\cos{k} + \frac{U}{2} (n \pm |\mathbf{m}|) \\
V &= \begin{pmatrix}
e^{-i\frac{\phi}{2}}\cos{\frac{\theta}{2}} & -e^{-i\frac{\phi}{2}}\sin{\frac{\theta}{2}} \\ 
e^{i\frac{\phi}{2}}\sin{\frac{\theta}{2}} & e^{i\frac{\phi}{2}}\cos{\frac{\theta}{2}}  
\end{pmatrix} \\
\theta &= \arctan{ \frac{m_z}{ \sqrt{m_x^2+m_y^2} } } \\
\phi &= \arctan{ \frac{m_y}{m_x} }
\end{align}

となる。

平均場の計算

$\mathbf{\gamma}(\mathbf{k}) = V^\dagger \mathbf{c}(\mathbf{k}) $とおくと、

\begin{align}
\langle c^\dagger_\sigma(\mathbf{R}) c_{\sigma'}(\mathbf{R}) \rangle 
&= \frac{1}{L} \sum_\mathbf{k,k'} \langle c^\dagger_\sigma(\mathbf{k}) c_{\sigma'}(\mathbf{k'}) \rangle e^{i(\mathbf{k'-k})\cdot \mathbf{R})} \\
 &= \sum_\mathbf{k} \sum_{nn'} V_{\sigma n}V^*_{n'\sigma'} \langle \gamma^\dagger_n(\mathbf{k}) \gamma_{n'}(\mathbf{k}) \rangle e^{i(\mathbf{k'-k})\cdot \mathbf{R})}
\end{align}

ここで対角化されているとき、

\langle \gamma^\dagger_n(\mathbf{k'}) \gamma_{n'}(\mathbf{k})\rangle =
\frac{ Tr[ \gamma^\dagger_n(\mathbf{k'}) \gamma_{n'}(\mathbf{k}) e^{-\beta H_{eff}} ] }{ Tr[ e^{-\beta H_{eff}}] }
= \delta_{nn'}\delta_\mathbf{kk'}f(E_n(\mathbf{k}))

となる(熱力学的平均のトレースをサイクリックに入れ替えて粒子の生成消滅演算子の交換関係を使う)。$f(E)$はフェルミ分布である。よって

\langle c^\dagger_\sigma(\mathbf{R}) c_{\sigma'}(\mathbf{R}) \rangle = \frac{1}{L} \sum_\mathbf{k} \sum_{n} V^*_{n\sigma}V_{\sigma'n}f(E_n(\mathbf{k}))

となり、ここで位置座標依存性が消えているので、$\langle c^\dagger_\sigma(\mathbf{R}) c_{\sigma'}(\mathbf{R}) \rangle$の$\mathbf{R}$は無視してもよいと分かる。さらに、$F(\mathbf{k}) = Diag[f(E_n(\mathbf{k}))]$とおくと、

\langle c^\dagger_\sigma c_{\sigma'} \rangle = \frac{1}{L} \sum_\mathbf{k} [VF(\mathbf{k}) V^\dagger]_{\sigma\sigma'} = G_{\sigma\sigma'}(n,\mathbf{m})

$n,\mathbf{m}$の自己無撞着方程式

\begin{align}
n &= \frac{1}{L} \sum_{\mathbf{k},\sigma} \sum_{n} V^*_{n\sigma}V_{\sigma n}f(E_n(\mathbf{k})) = Tr[G(n,\mathbf{m})]\\
m_i &= \frac{1}{L} \sum_{\mathbf{k},\sigma,\sigma'} \sum_{n} (\sigma_i)_{\sigma\sigma'} V^*_{n\sigma}V_{\sigma'n}f(E_n(\mathbf{k})) = Tr[\sigma_i G(n,\mathbf{m})]
\end{align}

を得る。

数値計算の方法

逐次代入法

簡単に先の自己無撞着方程式を$ (n,\mathbf{m}) = F(n,\mathbf{m})$と表すことにする。

まず適当な初期値$(n_0,\mathbf{m}_0)$として、適当な定数$\beta \in (0,1)$を用いて、

\begin{align}
(\tilde{n}_0,\tilde{\mathbf{m}}_0) &=  F(n_0,\mathbf{m}_0) \\
(n_1,\mathbf{m}_1) &= (1-\beta)(\tilde{n}_0,\tilde{\mathbf{m}}_0) + \beta(n_0,\mathbf{m}_0) \\
&\vdots\\
(\tilde{n}_p,\tilde{\mathbf{m}}_p) &=  F(n_p,\mathbf{m}_p) \\
(n_{p+1},\mathbf{m}_{p+1}) &= (1-\beta)(\tilde{n}_p,\tilde{\mathbf{m}}_p) + \beta(n_p,\mathbf{m}_p) \\
&\vdots
\end{align}

とする。これを誤差$\epsilon = |n_{p+1}-n_p|,|m^{i}_{p+1}-m^i_p|$($i=x,y,z$)が十分小さくなるまで繰り返す。

なぜ直接$(n_{p+1},\mathbf{m}_{p+1}) = F(n_p,\mathbf{m}_p)$としないかというと、これだと、最適解近傍で出力が振動しやすく、収束性が悪いからである。これを$\beta$の比で更新前の値との内分点を取ることで値の変化を抑制して防ぐのが目的である。この$\beta$はミキシングベータなどと呼ばれている。最適な$\beta$の値は問題によってまちまちだが、自分は例えば変化が大きい最初の$100$ステップくらいは$\beta\sim 0.1$くらいにして、その後は$\beta \sim 0.7$くらいまであげて使っている(今の問題は収束性がよいので、ミキシングを入れなくても問題ないと思う)。

ちなみにアンダーソンアクセラレーションという$p-1$の値も使って、$\beta$が誤差の低減とともに大きくなるように自動調整することで収束を早める方法もある。

個人的に一番おすすめなのは最初の$100\sim 1000$ステップくらいを割線法で更新して、その後にアンダーソン加速法に切り替えるやり方である。

化学ポテンシャル

一般にはフェルミ分布を計算する際に化学ポテンシャル$\mu$を決定する必要があるが、平均場$n,\mathbf{m}$が毎ステップごとに変化するので、化学ポテンシャルはステップごとに変化する。よって化学ポテンシャルを各ステップごとに求め直す必要がある。これは状態密度$D(E)$に対して粒子数$N(\mu) =\int_{-\infty}^\infty dE D(E)f(E)$とフィリング$\nu$に対して $N(\mu) < \nu\times(サイト数)\times(各サイトの状態数)$かどうかで二分探索すればよい。（以下の記事を参考にしてください。）

しかし、今の1/2フィリングハバード模型は粒子正孔対称性という良い性質があり、常に$\mu=\frac{U}{2}$となることが保証されているのでこの操作は必要ない。

大域性

一般に逐次代入法で求めた解は局所安定解になっていて、最適解ではない可能性がある。これを回避するためにいくつかの初期値からシミュレートしてそれぞれの解を比較する必要がある。この比較ではヘルムホルツ自由エネルギーを各々の場合で計算してよりエネルギーの低い方を採用すればよい。なぜならギブス・ボゴリューボフ・ファインマンの不等式というものがあって、ざっくり言うと近似したハミルトニアンから求めたヘルムホルツ自由エネルギーはも元のものより大きくなるからだ。つまり、より低い自由エネルギーのものが最適解に近いことになる。
今の例では局所解に引っかかることがないので、今回はこの過程は省く。

自由エネルギーの式

ヘルムホルツの自由エネルギーは次のように計算される：

\begin{align}
F &= -k_B T \sum_{\mathbf{k},n} \log \left( 1+e^{-\frac{E_n(\mathbf{K})-\mu}{k_B T}} \right) + N \mu_{before} \\
& - NU\sum_{\sigma} \langle c^\dagger_\sigma c_\sigma \rangle \langle c^\dagger_{-\sigma} c_{-\sigma} \rangle + NU\sum_{\sigma} \langle c^\dagger_{-\sigma} c_\sigma \rangle \langle c^\dagger_{\sigma} c_{-\sigma} \rangle \\
&= -k_B T \sum_{\mathbf{k},n} \log \left( 1+e^{-\frac{E_n(\mathbf{K})-\mu}{k_B T}} \right) + N \mu_{update}
\end{align}

ここで$\mu_{before}$は更新前の化学ポテンシャル、$\mu_{update}$は更新後の化学ポテンシャルである。ただしこの式の計算はオーバーフローやアンダーフロー、情報落ち、桁落ちなどの数値誤差による異常が起きやすいので注意が必要である。

使用する平均場

平均場がずっとゼロと分かっていたり、本質的でない場合は平均場をいくつか削って考えることがある。
例えば今のケースはフォック項を削って$n,m_z$だけ考えることもある。フォック項は$m_x,m_y$を与えるが、例えば次の例のシステムは等方的なので、どの向きにでも磁化が発生する可能性が同様にあって(自由エネルギーは同じ)方向はあまり重要ではない。よってフォックを落として$z$方向に磁化が出ると決め打ってしまっても大丈夫である。

実装

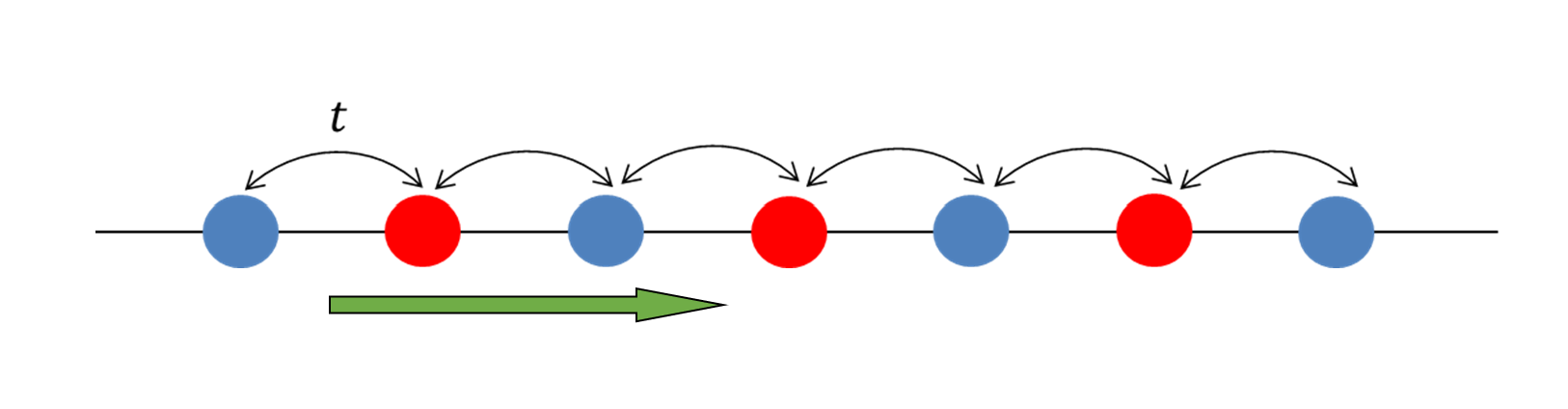
ここでは反強磁性転移をシミュレーションしてみよう。そのためには格子の扱いを図のようにリスケールしなくてはいけない。

$2\mathbf{a}$を基本並進ベクトルに取り直して(図の緑矢印)、副格子$a,b$(赤/青のサイト)を使ってハバード模型を変形する。このとき、サイトA,Bの副格子位置は$\pm a/2$とした。
また、簡単のために今回はハートリー項だけ考えることにする。先と同様に平均場近似すると

\begin{align}
\mathbf{c}(\mathbf{k}) &= \begin{pmatrix}
a_\uparrow(\mathbf{k}) & a_\downarrow(\mathbf{k}) & b_\uparrow(\mathbf{k}) & b_\downarrow(\mathbf{k})
\end{pmatrix}^T \\

H_{eff}(\mathbf{k}) &= \sum_\mathbf{k} \mathbf{c}^\dagger(\mathbf{k}) \begin{pmatrix}
U\langle a^\dagger_\downarrow a_\downarrow \rangle & 0 & 2t\cos{k/2} & 0 \\
0 & U\langle a^\dagger_\uparrow a_\uparrow \rangle & 0 & 2t\cos{k/2} \\
2t\cos{k/2} & 0 & U\langle b^\dagger_\downarrow b_\downarrow \rangle & 0 \\
0 & 2t\cos{k/2} & 0 & U\langle b^\dagger_\uparrow b_\uparrow \rangle
 \end{pmatrix} \mathbf{c}(\mathbf{k})
\end{align}

となる。
サイトA,Bの磁化

m_A = \langle a^\dagger_\uparrow a_\uparrow \rangle - \langle a^\dagger_\downarrow a_\downarrow \rangle \\
m_B = \langle b^\dagger_\uparrow b_\uparrow \rangle - \langle b^\dagger_\downarrow b_\downarrow \rangle

の温度依存性を計算するコードを実装しよう。

まずヘッダーでnumpyを読み込む

hartree.py

import numpy as np
from numpy import linalg as LA
from nptyping import NDArray

またパラメーターは以下の通り

hartree.py

site = 128 #サイト数
size = 4 #行列の自由度
t=1. #重なり積分
U=4. #相互作用

次はフェルミ分布関数を用意する

hartree.py

def calc_boltzmann_factor(energy:float, kbt:float):
    inv_temp = 1/(kbt)
    a = -inv_temp*(energy)
    if a > 709: #prevent overflow
        a = 709
    elif a < -745: #prevent underflow
        a = -745
    return np.exp( a )

def fermi(kbt:np.float64,energy:np.float64,mu=0.5*U):
    return 1/(calc_boltzmann_factor(mu-energy, kbt)+1)

有効ハミルトニアンは

hartree.py

def H_eff(k,mean):
    hop = 2 * t * np.cos( k/2 )
    #(A,up),(A,down),(B,up),(B,down)
    h = np.array([
        [ 0, 0, hop, 0 ],
        [ 0, 0, 0, hop ],
        [ hop, 0, 0, 0 ],
        [ 0, hop, 0, 0 ]
    ])
    h_int = U*np.diag([ mean[1], mean[0], mean[3], mean[2] ])
    return h + h_int

であり、$mean = (\langle a^\dagger_\uparrow a_\uparrow \rangle , \langle a^\dagger_\downarrow a_\downarrow \rangle , \langle b^\dagger_\uparrow b_\uparrow \rangle , \langle b^\dagger_\downarrow b_\downarrow \rangle)$となっている。

逐次代入は

hartree.py

def update__init__(energy,uni):
    f = np.diag(np.array([ fermi(kbt,E) for E in energy ]))
    return np.diag(np.conj(uni).dot(f).dot(uni.T))
    #LA.eigの出力はrow-majorなので、uniは横向きの固有ベクトルを並べた行列
    #この行列の対角成分がハートリー項、非対角の同じサイト同士の成分がフォック項である。


def update(kbt:np.float64,mean):
    mean_new = np.zeros(size).astype('float64')
    for i in range(site):
        k = 2*np.pi*i/site
        E,uni = LA.eigh(H_eff(k,mean))
        mean_new += update__init__(E,uni)
    return mean_new/site

def self_consist(m_ini:NDArray[size,np.float64], kbt:np.float64, b:np.float64, th:np.float64 ):
    m1 = m_ini
    err = 1+th;
    while(err>th):
        m2 = b*m1 + (1-b)*update(kbt,m1)
        err = np.sum(np.abs(m2-m1))
        m1 = m2.copy()
    return m1

で行う。以上の関数を使って実行する部分は

hartree.py

th=1e-3 #閾値
b=0.5 #ミキシングベータ

temp_arr = np.linspace(1/32,2,128)
m_ini = np.random.rand(size)
m1_list = []
m2_list = []
step = 0
for kbt in temp_arr:
    mean = self_consist(m_ini,kbt,b,th)
    m_ini = mean.copy() #ひとつ前の温度の結果を次の初期値にする
    m1_list.append(mean[0]-mean[1])
    m2_list.append(mean[2]-mean[3])

である。各温度に対してm1_listにAの磁化、m2_listにBの磁化を格納する。また隣の温度点の結果を初期値に使って次の温度の計算を行う。各温度点で独立に計算すると、磁化の符号が反転する可能性があるのでそれを防ぐためである。

次で結果を出力する。

hartree.py

from matplotlib import pyplot as plt 

plt.plot(temp_arr,m1_list)
plt.plot(temp_arr,m2_list)
plt.axhline(y=0,color="black",linestyle="--",lw=0.5)
plt.axvline(x=0.86,color="black",linestyle=":",lw=0.5)
plt.xlim([0,2])
plt.xlabel("temperature")
plt.ylabel("magnetization")
plt.savefig("hartree.png")

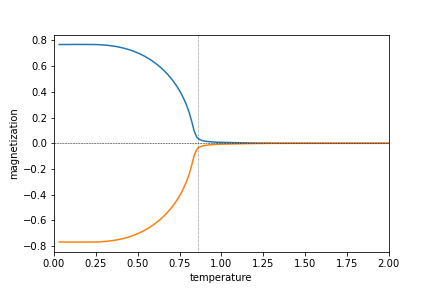
次図のように確かにA,Bサイトで逆向きに磁化が生じている。

転移点近傍の高温側でずるずると有限の磁化が出ているが、これは低温側の隣の計算結果からスタートしたために、準安定解に収束してしまうからである。いくつかの初期値からスタートして比較することでこうしたエラーは防ぐことができる。

コメント

• 分かりやすさ重視でpython3を使ったが、２次元以上になるとかなり遅い(while文のせいなのか？)。自分で使う場合はc++やjuliaなどで実装することをおすすめする(システムの複雑さにもよるが、僕の経験ではc++なら２次元でもストレスのない速度で動く)。
• ハーフフィリングに限定したが、フィリングによっても出てくる相が変化する。化学ポテンシャルを求めるパートを追加し、２次元正方格子ハバード模型などで試してみてほしい(参考文献参照)。

参考文献

• https://journals.aps.org/prb/abstract/10.1103/PhysRevB.31.4403