最初に
システム開発において、特に大規模なリクエスト量が見込まれるアプリケーションを作成する際には、実際のリクエスト量を模擬した性能負荷テストも実施する。
過去に参加してきた性能負荷テストにおいて、目標値に関して、勘違いをして議論をしている場合があるため、この記事を書いてみた。
スループット(TPS)と並行数
よく性能負荷テストを議論するときに、スループット(TPS)と並行数を混同して議論をしていることがある。
ここではそれぞれの言葉の定義を再度書く。
- スループット(TPS)
単位時間辺りに処理できるトランザクション数。
通常単位時間には秒を用いることが多いため、秒あたりのトランザクション数としてTPS(Transaction Per Secend)とも表現される。
スループットの値が大きいことは、多くのトランザクションが処理できていることを意味する。
- 並行数
ある時点に置いて、どれだけのトランザクションが処理されているか。
こちらは単位としては、トランザクション数である。
並行数が大きいことは、ある時間において、多くの処理が同時にできていることを意味する。
ややこしくしている原因は、スループットも並行数も大きい値は多くの処理ができていることを示す概念であることである。
実例で説明しましょう。
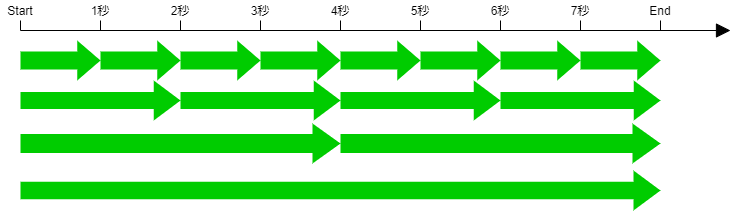
1つめのケースは1秒ごとに2つのリクエストが送信され、それぞれのリクエストは1秒で終了するケース。
このケースではどの時点でも並行数は2で、スループットは1秒あたり2トランザクションである。
2つめのケースは2秒ごとに2つのリクエストが送信され、それぞれのリクエストは2秒で終了するケース。
このケースでもどの時点でも並行数は2であるが、スループットは2秒あたり2トランザクションで、1秒あたりで換算すると1トランザクションである。
さて、この2つはともに並行数は2であるが、スループットには差がついた。この差の要因は、応答時間であることは一目瞭然だと思う。
まとめると以下である。並行数は変わらないが、スループットが伸びると、応答時間が少なくなっている。
| ケース | 並行数 | スループット(TPS) | 応答時間(秒) |
|---|---|---|---|
| ケース1 | 2 | 2 | 1 |
| ケース2 | 2 | 1 | 2 |
賢明な方は気がつくと思うが、これらの数値には関係性がある。
リトルの法則
リトルの法則とはWikipediaによれば、待ち行列理論で以下の数式で表される。
L = \lambda W
ここで、$L = 顧客数$、$\lambda = 到着数$、$W=顧客が費やす時間$ である。
この数式は待ち行列理論の意味合いで表される。そのため、一見無関係に思えるが、性能負荷テストの場合は以下の数式で表すことができる。
並行数 = スループット \times 応答時間
先ほどのケース1/ケース2にあてはめると、下記のとおりである。
- ケース1
2_{並行} = 2_{tps} \times 1_{秒}
- ケース2
2_{並行} = 1_{tps} \times 2_{秒}
この2つのケースだと、簡単すぎるので、少し複雑な例を考えてみる。
この例では4並行で稼働していることはすぐに分かる。そのため、スループットと平均応答時間の乗算が4になるはずであるが、それを検証してみる。
まず、スループットは1行目8トランザクション、2行目4トランザクション、3行目2トランザクション、4行目1トランザクションの合計15トランザクションが8秒の間に到着している。つまり、$\frac{8 + 4 + 2 + 1}{8} = 15/8 = 1.875_{tps}$である。
平均応答時間は以下のとおり。(添字のtranはトランザクションの意味)
\frac{1_{秒} \times 8_{tran} + 2_{秒} \times 4_{tran} + 4_{秒} \times 2_{tran} + 8_{秒} \times 1_{tran} }{15_{tran}} = \frac{32_{秒Tran}}{15_{Tran}}=2.133 秒
これらを掛け合わすと以下のとおり4(並行)となる。
1.875_{tps} \times 2.133_{秒} \fallingdotseq 4.00_{並行}
これは分数で計算すると、より正確である。
\frac{15}{8}_{tps} \times \frac{32}{15}_{秒} = 4_{並行}
改めてスループット/並行数/応答時間
リトルの法則をもう一度見直しみよう。
並行数 = スループット \times 応答時間
この数式を見る限り、並行数を上げるには、スループットを上げるか、応答時間を上げるかで達成できる。
スループットを上げることで並行数が上がることは理解がしやすいと思うが、同一スループットで応答時間が上がることで並行数が上がることもイメージを持っておくことが重要である。
スループットを中心とした式は以下の通り。
スループット = \frac{並行数}{応答時間}
スループットを上げるには、並行数を上げるか、応答時間を 下げるか で達成できる。これはいずれも直感どおりではないかと思う。
応答時間を中心とした式は以下の通り。
応答時間 = \frac{並行数}{スループット}
応答時間を 下げる には並行数を下げるか、スループットを上げることで達成できる。応答時間を並行数やスループットと関係してイメージできることが重要である。
まとめ
並行数/スループット/応答時間はそれぞれリトルの法則に基づき理解をすると、性能負荷検証において、より正確で深い理解ができるようになるので、是非使ってみてください。