数学カフェのLTで話す予定でしたが、使う機会がなくなったので公開します。
Haskellにおけるモナドとは
HaskellではMonadという型クラスでモナドを表現しています。この型クラスは return :: a -> m a 、 join :: m (m a) -> m a 、そして fmap においてモナドが表現されています。色んな人が色んな場で説明していることですから、今さらここで議論を掘り返す必要はないでしょう。
モナドには []、Maybe、State s、Cont r、Reader r、Writer w、IO、などがあります。しかし、みなさんはそれで満足でしょうか? そんなモナドで大丈夫ですか?
Haskellでもっとモナド
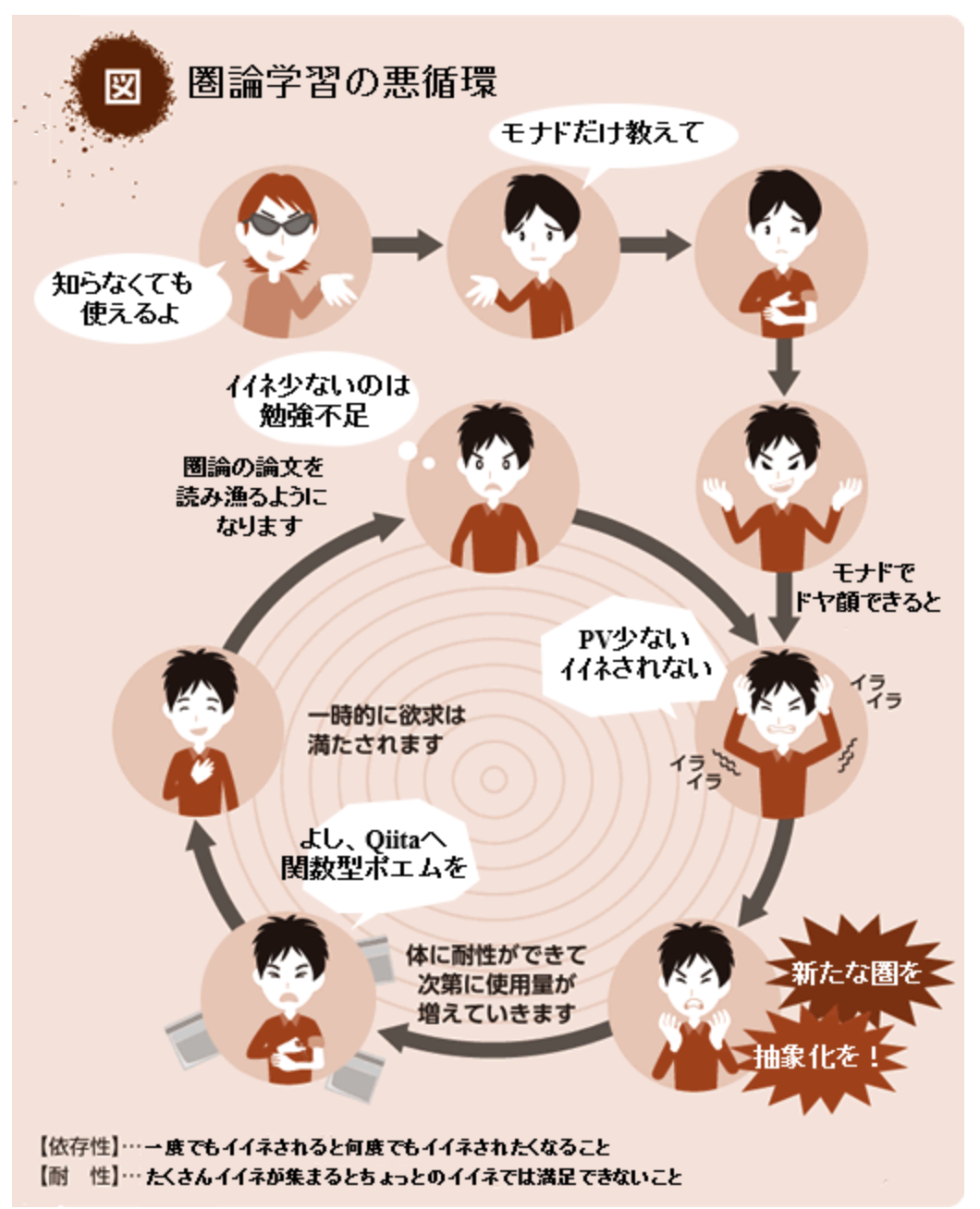
モナドをさらにこじらせた人は、 Free モナドや Codensity モナドなどに手を出すでしょう。これらは大変便利なものですが、その珍しさ故これまた多くの場所ですでに語られています。次の図を見てもわかるように、一度モナドを触り始めると人は際限なく満足できなくなってしまうのです。
モナドで満足できなくなってしまった人のためのモナドモナド
普通のモナドに満足ができなくなった方は、モナドモナドに触れてみるのはいかがでしょうか? モナドモナドが公の場で語られているところを私は見たことはありませんが、 mmorphパッケージのControl.Monad.Morphにおいて、 MMonad 型クラスで密かに定義されています。 Monad 型クラスとは別のものです。
このモナドモナドとはなんでしょうか? モナドは特定の性質を持つ、 Hask 圏における自己関手でした。ところが、モナドはさらに新たな圏の構造を持っています。自己関手は自然変換を射と見なせば圏を構成します。モナドは自己関手に演算を入れたものですので、その演算を保持するような自然変換と組み合わせることで圏をなします。モナドの性質を保存する自然変換を、モナドモーフィズムと呼びます。mmorphの語源ですね。
圏が存在すれば、そこには自己関手、そしてモナドが存在する可能性があります。 MMonad は、モナドが成す圏(対象がモナド、射がモナドモーフィズム(自然変換))上の自己関手によるモナドです。
MMonadの持つ演算
MMonadはモナドなので、単位元と積を持ちます。単位元(return)に該当するのは lift :: Monad m => m a -> t m a という関数です。型を見て分かる通り、モナド m を t m というモナドへ移します1。そして、積(join)に該当するのは squash :: (Monad m, MMonad t) => t (t m) a -> t m a です。t t mと入れ子になったモナドモナドtを、 t m へ潰します。
モナドは関手なので射関数(fmap)に該当する対応も必要ですね。これは hoist :: (Monad m, MFunctor t) => (forall a . m a -> n a) -> t m b -> t n b です。モナドの圏の射は自然変換なので、Haskの射を移すだけの fmap とは違って Rank2Types が必要となります。
lift の正体
モナドモナドの単位元である lift に見覚えのあるモナド常習者の方もいらっしゃるかもしれません。この lift は、モナド変換子の lift そのものです。モナドモナドの視点から見ると、モナド変換子はモナドモナドの性質をかなり弱めたものです。一般論ではモナド変換子は lift の存在しか要請しておらず、関手 MFunctor にすらなっていません。これは条件を厳しくすると ContT がモナド変換子になってくれないためです。 ContT は継続を表す実用上は重要な変換子であるため、これをモナド変換子と言えないのは問題です。
モナド変換子の分類については、モナドモナドを使うよりもモノイダル関手を使って分類したほうがきれいにまとまると個人的には思っています。詳しくは モナモナ言うモナド変換子入門 を参照して下さい。
モナドモナドの使い道
モナド変換子のうち MMonad のインスタンスになるものについて、モナドと同じ感覚で使うといいでしょう。モナドを使い慣れていれば、mの代わりにtを同じ感覚で変更できると思えば有意義に使えるはずです。例えば squash はモナド (t m) (t m) を潰すわけではなく、モナド変換子 t t を直接潰すことができます。詳しくは mmorphのチュートリアル を見るといいでしょう。
最後に
モナドモナドはLTでウケを狙うために作った造語で、そういう言い方をすることはありません。 MMonad の考え方自体は圏論とHaskellの表現力を見るという点では面白いので、興味がある人は追っかけてみるのもいいでしょう。
-
圏論的に見る場合、モナドの場合関数
returnが対象aについてのコンポーネントでしたが、ここでは自然変換liftが対象mのコンポーネントとなることに注意しましょう。 ↩