はじめに
某インターンで制作物のプレゼンをする必要があったため、一年生の頃に作ったゲームをつい最近アップデートしました。
そこで新たに実装した機能の実装方法を解説しようと思い、この記事を書いています。
せっかくなのでUnity講座の一環としてしまおうということで書いていますが、前回までの内容に比べ、内積・外積といった数学的な内容のものも含んでいるので、前提知識がないとちょっと厳しいかもしれません。
数学のお話はなるべく補足説明を入れて解説しようと思いますが「分からない」とか「間違いがあるよ」などなどあればコメントください。
それでは解説に入っていきましょう。
機能概要
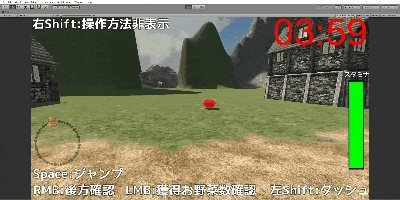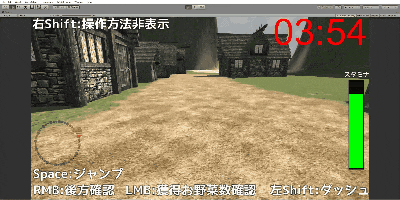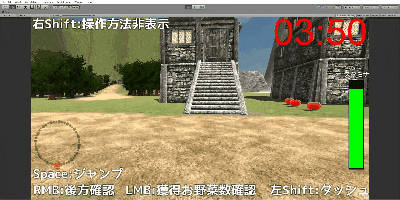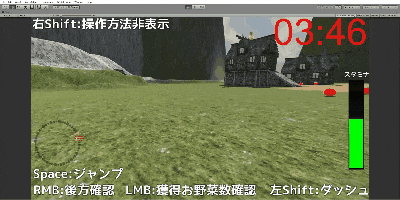
自分のゲームは簡単に言うと敵が追ってきて、捕まるとゲームオーバーというゲームです。
したがって、どのくらい近いかを確認したりしたいですが、ミニマップのようなものを作ってしまうと簡単になりすぎてしまうかなと考えました。
これまでの機能として、後方確認はいつでもできましたが、壁の向こう側にいたりすると全く気づけませんでした。
そこで、方向だけは常に分かるようにしようと考えました。
方角だけでもわかれば逃げやすくなるだろうということですね。
一応距離をついでに表示させたりも考えましたが、そこまで来るとミニマップと変わらないかなぁと思って、今回は実装を見送りました。
自分のゲームでは追ってくる敵に対してコンパスを適用していますが、ゴール地点だったり、アイテムを目標にすることも可能ですので、使えるゲームジャンルは割と広いかなと思っています。
それでは早速実装に入っていきましょう。
前準備(Canvas&デバッグ用)
まず最初に、コンパスのリングとデバッグ用のテキストを準備しました。
console.log()はたしかに便利なのですが、プレイ中に確認しにくいのと、Update内で実行している処理で呼び出すと、ログが埋まってしまうので、実装中は画面に数値を表示することをおすすめします。

空オブジェクトのEnemyCompassの直下にUI/Textを作ります。
今回は名前を変えていませんが、プロジェクト内に既に複数のTextが存在しているならば、EnemyCompassDebugTextとかに変更しておいたほうがいいかもしれません。
あとはコンパスのフレームに使えそうな素材を見繕ってきました。
「円形フレーム」などで検索すれば、他にもいろいろな素材サイトが見つかると思うので、自分好みのフレームを探してきてください。

今回のコンパスでは下手に色がついているよりは黒単色のほうがいいかな、と思いImageのColorを黒にしました。
コンパスの後ろの画面を隠さないように、アルファ値をを100くらいにして半透明にしておきましたが、別に気にならないという方は変更しなくても大丈夫です。
人によって違うので割愛しますが、ここで目標物のアイコンなどの素材を準備して、置いておくといいと思います。
ここまでできればコンパス機能の見た目は大丈夫かなと思います。
目標物との角度計算
内積・外積
さて、ここからは数学のお時間です。
流石にベクトルの話からするのは大変なので、高校数学の美しい物語などを確認してもらうとします。
今回は実装方法の話をしたいので、なぜこうなるかについては解説しません。
気になる方はベクトルの勉強をしてみてください。
コンパス機能を実装するためには、自分の正面方向のベクトルと目標物への方向ベクトルのなす角の大きさを計算する必要があります。
正面方向のベクトルは
Player.transform.forward
で、目標物への方向ベクトルは
Target.transform.position-Player.transform.position
で求めることができますね(ベクトルABの求め方は原点をOとしてベクトルOB - ベクトルOAで求めるという公式)
この2つのベクトルのなす角の大きさを調べるのに、内積や外積が役に立つのです。
※一応図を自作しましたが正直出来はいまいちなので、参考リンクの画像などを参照してください
内積は2つのベクトルの各成分の掛け算を取ります。
↑a・↑b=a.x*b.x+a.y*b.y
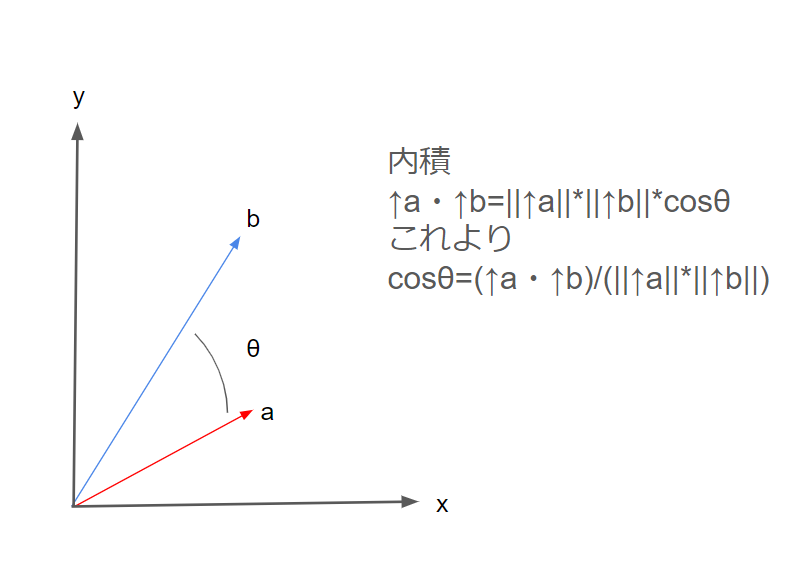
上の式と、この図で示した式を使うことで、2つのベクトルのなす角の大きさをθとしたとき、cosθを求めることができるのです。
今回は3Dゲームなのでy方向の情報もありますが、今回はy方向の情報を切り捨てて二次元の内積を求めてくれる関数、dot_2dを作成しました。
公式ではaベクトルの大きさとbベクトルの大きさを掛けた上で内積の大きさを割っていますが、どちらのベクトルも正規化を行い、大きさを1にしてから計算することで手間を省けます。
float dot_2d(Vector3 aVec, Vector3 bVec)
{
return (aVec.x * bVec.x + aVec.z * bVec.z);
}
さて、これだけでコンパスができると思いきや、cos関数はcosθ=cos(-θ)という厄介な(ときには便利な)性質があります。
つまり、なす角の大きさはわかっても、正面から見て右に向かう角の大きさなのか、左に向かう角の大きさなのか区別がつかないのです。
そこで使うのが外積です。
こっちは大学数学の内容なので知らない人のほうが多いと思いますが、これを知らずにゲームを作るのはすごく難しいと言うくらい、使えるものです。
こっちは外部サイトの図を見てきてくださいと言う形になりますが、求めることで2つのベクトルのなす角の大きさをθとしたときに、sinθを求めることが出来ます。
内積と違い、2次元と3次元で意味が違います。
2次元のときにはaベクトルとbベクトルで作られる平行四辺形の面積を、3次元ではaベクトルとbベクトルのなす平面の法線ベクトルを求めます。
面積(数値)と法線ベクトル(ベクトル)というように、結果の単位が変わるのは面白いですね。
外積は、内積と違ってマイナスの値も取ります。
また、aベクトルとbベクトルの外積と、bベクトルとaベクトルの外積の値は違うというように、演算の順序が関係してきます。
aベクトルとbベクトルの外積は、aベクトルをx軸正の方向と重なるように置いたとき、
偏角が0からπの間なら正の値に、
偏角がπから2πの間なら負の値になります。
偏角が0やπのときは、2つのベクトルが平行になるので、0になります。
こちらも、y方向の情報を切り捨てて外積を計算してくれる関数、cross_2dを作成しました。
float cross_2d(Vector3 aVec,Vector3 bVec)
{
return (aVec.x * bVec.z) - (aVec.z * bVec.x);
}
実装に使ってみる
※2020/10/27更新 ここから
もっと簡単でわかりやすい実装方法を思いついてしまったので更新しておきました。
最下部に追記で更新バージョンのプログラムを置いておきますが、以前に書いた部分は消さずに残しておきます。
せっかちな方は飛ばしてください
※2020/10/27更新 ここまで
内積と外積を使うことで、2つのベクトルのなす角の大きさθについて、cosθとsinθの値を求めることが出来ました。
この2つの情報を使うことで、偏角が第何象限にあるかを調べることが出来ます。
そうすればあとはAsinやAcosを用いて、偏角θを求めることが出来ます。
var PlayerForward = Player.transform.forward;
var ToEnemyVec = Enemy.transform.position - Player.transform.position;
ToEnemyVec = ToEnemyVec.normalized;
float SinPlayerToEnemy = cross_2d(PlayerForward, ToEnemyVec);
float CosPlayerToEnemy = dot_2d(PlayerForward, ToEnemyVec);
//第何象限に敵が位置しているか
int State = 0;
//第一象限のとき
if (SinPlayerToEnemy > 0 && CosPlayerToEnemy > 0)
{
State = 0;
}
//第二象限のとき
else if (SinPlayerToEnemy > 0 && CosPlayerToEnemy < 0)
{
State = 1;
}
//第三象限のとき
else if (SinPlayerToEnemy < 0 && CosPlayerToEnemy < 0)
{
State = 2;
}
//第四象限のとき
else if (SinPlayerToEnemy < 0 && CosPlayerToEnemy > 0)
{
State = 3;
}
float Rad = Mathf.Asin(SinPlayerToEnemy);
//Asinでは(-π/2,π/2)の範囲しか表せないので、象限によって範囲を(-π,π)に拡張する
switch (State)
{
case 0:
break;
case 1:
Rad = Mathf.PI - Rad;
break;
case 2:
Rad = -Mathf.PI - Rad;
break;
case 3:
break;
}
RadText.text = "Rad:" + Rad;
RadTextが宣言なしに出てきていますが、ここは最初で設定したデバッグ用テキストのTextを変更するように自分で変えてみてください(一応最後にプログラム全体を載せるので参考にしてください)。
別の使いみちをしている方はEnemyを適当な変数名に変更して使ってください。
UI更新
さて、これで目標物への角度を求めることが可能になりました。
しかし、この情報を使ってUIを更新してあげないと使えませんよね。
ここまでついてこれた人なら簡単だと思いますが、UIの更新には求めた偏角を使って、
目標物の画像の位置を(x,y)=(cosθ,sinθ)にしてあげれば大丈夫です。
ただ、このままだと半径が1の単位円上を動くので、UIとしては動きが小さいです。
適当な長さを掛けてあげて、コンパスのリング部分の画像とうまく合うように調整してください。
Vector3 ImageTransform = new Vector3(uiImageRadius * Mathf.Cos(Rad), uiImageRadius * Mathf.Sin(Rad), 0);
EnemyImage.rectTransform.localPosition = ImageTransform;
さて、これで実行してみるとうまくいかないはずです。
90度分右にずれていませんか?
ピンときた方もいるかもしれませんが、二次元平面を半径と偏角を用いて表すときを思い出してみましょう。
偏角は、x軸正方向から反時計回りに動いていきましたね。
つまり、UIではプレイヤーの正面が始まりとして考えているのに、偏角はプレイヤーの右方向を始まりとして計算されてしまっているのです。
対策方法は簡単で、最終的に計算された偏角にπ/2を足してあげればいいだけですね。
つまり正しい形でのUIの更新処理はこの様になります。
//プレイヤーの正面始まりなので、表示のための計算にはラジアンをπ/2だけ移動させる
float RadOffset = Mathf.PI / 2;
Rad += RadOffset;
Vector3 ImageTransform = new Vector3(uiImageRadius * Mathf.Cos(Rad), uiImageRadius * Mathf.Sin(Rad), 0);
EnemyImage.rectTransform.localPosition = ImageTransform;
完成形
自分のゲームでは難易度によって敵の数が変わり、複数体の敵に対応する必要があったため、UIの画像の位置更新処理を関数に分割しました。
そのため、参考にならない部分もあるとは思いますが、なるべくわかりやすくコメントをしたので、取捨選択をして、自分のゲームに組み込んでみてください。
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
using UnityEngine.UI;
public class EnemyCompassControl : MonoBehaviour
{
private GameObject Player;
private GameObject Burger;
private GameObject Fries;
private GameObject Drink;
//private Text RadText;
[SerializeField]
private Image BurgerImage;
[SerializeField]
private Image FriesImage;
[SerializeField]
private Image DrinkImage;
[SerializeField]
[Tooltip("敵のイメージを表示させる円の半径")]
private float uiImageRadius=180;
//private Text RadText;
// Start is called before the first frame update
void Start()
{
Player = GameObject.FindWithTag("Player");
Burger = GameObject.FindGameObjectWithTag("Burger");
Fries = GameObject.FindGameObjectWithTag("Fries");
Drink = GameObject.FindGameObjectWithTag("Drink");
//RadText = GetComponentInChildren<Text>();
}
// Update is called once per frame
void Update()
{
UpdateEnemyImage(Burger, BurgerImage);
if (Fries != null && Fries.activeInHierarchy)
{
UpdateEnemyImage(Fries, FriesImage);
}
else
{
FriesImage.enabled = false;
}
if (Drink != null && Drink.activeInHierarchy)
{
UpdateEnemyImage(Drink, DrinkImage);
}
else
{
DrinkImage.enabled = false;
}
}
float cross_2d(Vector3 aVec,Vector3 bVec)
{
return (aVec.x * bVec.z) - (aVec.z * bVec.x);
}
float dot_2d(Vector3 aVec, Vector3 bVec)
{
return (aVec.x * bVec.x + aVec.z * bVec.z);
}
void UpdateEnemyImage(GameObject Enemy,Image EnemyImage)
{
var PlayerForward = Player.transform.forward;
var ToEnemyVec = Enemy.transform.position - Player.transform.position;
//正規化することで角度を求めるときに大きさで割るのを省略する
ToEnemyVec = ToEnemyVec.normalized;
float SinPlayerToEnemy = cross_2d(PlayerForward, ToEnemyVec);
float CosPlayerToEnemy = dot_2d(PlayerForward, ToEnemyVec);
//第何象限に敵が位置しているか
int State = 0;
//第一象限のとき
if (SinPlayerToEnemy > 0 && CosPlayerToEnemy > 0)
{
State = 0;
}
//第二象限のとき
else if (SinPlayerToEnemy > 0 && CosPlayerToEnemy < 0)
{
State = 1;
}
//第三象限のとき
else if (SinPlayerToEnemy < 0 && CosPlayerToEnemy < 0)
{
State = 2;
}
//第四象限のとき
else if (SinPlayerToEnemy < 0 && CosPlayerToEnemy > 0)
{
State = 3;
}
float Rad = Mathf.Asin(SinPlayerToEnemy);
//RadText.text = "Rad:" + Rad;
//Asinでは(-π/2,π/2)の範囲しか表せないので、象限によって範囲を(-π,π)に拡張する
switch (State)
{
case 0:
break;
case 1:
Rad = Mathf.PI - Rad;
break;
case 2:
Rad = -Mathf.PI - Rad;
break;
case 3:
break;
}
//プレイヤーの正面始まりなので、表示のための計算にはラジアンをπ/2だけ移動させる
float RadOffset = Mathf.PI / 2;
Rad += RadOffset;
Vector3 ImageTransform = new Vector3(uiImageRadius * Mathf.Cos(Rad), uiImageRadius * Mathf.Sin(Rad), 0);
EnemyImage.rectTransform.localPosition = ImageTransform;
}
}
さいごに
実装してる自分ではわかることでも、人に伝えるために説明し直すのはやはり大変ですね。
正直、同じ内積・外積を使うやり方でも、より簡単な処理方法があるのではないかとも考えています。
もしこういう処理はどうかな?みたいに思ったことがありましたら、コメントなど頂けるとありがたいです。
ここが分からなかった、という意見でもいいので、どうぞ気軽にコメントを下さい。
もっと簡単な実装方法(2020/10/27追記)
当初の実装にコメントで補足していますが、Asinでは(-π/2,π/2)の範囲しか表せません。
そこで、cosとsinの値を使って象限がどこに位置するかを調べて(-π,π)の範囲に拡張していたわけです。
ですが、よくよく考えてみればそんなことをする必要はなかったのです。
Asinの代わりにAcosを使ってみたらどうでしょうか。
Acosは(0,π)の範囲を取ります。そして、sinの値によって偏角が正方向なのか負方向なのか判断できます。
...はい、これで終わりです。
なんでこの記事を書いていたときの自分はこんな簡単なことに気づかなかったんでしょうか。
自分語りはこれくらいにしてもう一度スクリプト全体を載せます。
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
using UnityEngine.UI;
public class EnemyCompassControl : MonoBehaviour
{
private GameObject Player;
private GameObject Burger;
private GameObject Fries;
private GameObject Drink;
//private Text RadText;
[SerializeField]
private Image BurgerImage;
[SerializeField]
private Image FriesImage;
[SerializeField]
private Image DrinkImage;
[SerializeField]
[Tooltip("敵のイメージを表示させる円の半径")]
private float uiImageRadius=180;
//private Text RadText;
// Start is called before the first frame update
void Start()
{
Player = GameObject.FindWithTag("Player");
Burger = GameObject.FindGameObjectWithTag("Burger");
Fries = GameObject.FindGameObjectWithTag("Fries");
Drink = GameObject.FindGameObjectWithTag("Drink");
//RadText = GetComponentInChildren<Text>();
}
// Update is called once per frame
void Update()
{
UpdateEnemyImage(Burger, BurgerImage);
if (Fries != null && Fries.activeInHierarchy)
{
UpdateEnemyImage(Fries, FriesImage);
}
else
{
FriesImage.enabled = false;
}
if (Drink != null && Drink.activeInHierarchy)
{
UpdateEnemyImage(Drink, DrinkImage);
}
else
{
DrinkImage.enabled = false;
}
}
float cross_2d(Vector3 aVec,Vector3 bVec)
{
return (aVec.x * bVec.z) - (aVec.z * bVec.x);
}
float dot_2d(Vector3 aVec, Vector3 bVec)
{
return (aVec.x * bVec.x + aVec.z * bVec.z);
}
void UpdateEnemyImage(GameObject Enemy,Image EnemyImage)
{
var PlayerForward = Player.transform.forward;
var ToEnemyVec = Enemy.transform.position - Player.transform.position;
//正規化することで角度を求めるときに大きさで割るのを省略する
ToEnemyVec = ToEnemyVec.normalized;
float SinPlayerToEnemy = cross_2d(PlayerForward, ToEnemyVec);
float CosPlayerToEnemy = dot_2d(PlayerForward, ToEnemyVec);
float Rad = Mathf.Acos(CosPlayerToEnemy);
if (SinPlayerToEnemy < 0) Rad *= -1;
//プレイヤーの正面始まりなので、表示のための計算にはラジアンをπ/2だけ移動させる
float RadOffset = Mathf.PI / 2;
Rad += RadOffset;
Vector3 ImageTransform = new Vector3(uiImageRadius * Mathf.Cos(Rad), uiImageRadius * Mathf.Sin(Rad), 0);
EnemyImage.rectTransform.localPosition = ImageTransform;
}
}