全プログラマに捧ぐ！図解「パターンマッチ」

パターンマッチを使い始めてかなりの時間が経ちました。最初は関数型言語の一機能として触り始めましたが、徐々に関数型言語のユーザだけの玩具にしておくのは勿体ないと思うようになってきました。プログラミングにおいて、パターンマッチほど有用であるにもかかわらず普及が遅れている言語機能は他にないと思います。
本記事ではその状況に一石を投じたく、一般のプログラマにも伝わるようになるべく図解で「パターンマッチ」を解説してみたいと思います。

(本記事は自分のブログからの転載記事です。)

はじめに

本記事はプログラミング言語における「パターンマッチ」¹という機能に着目して解説したものです。「パターンマッチ」は、switch文の強化版²であり、仮にパターンマッチを持たないプログラミング言語のユーザだとしても全プログラマが知っていて損はないアイデアだと思います。

パターンマッチとは

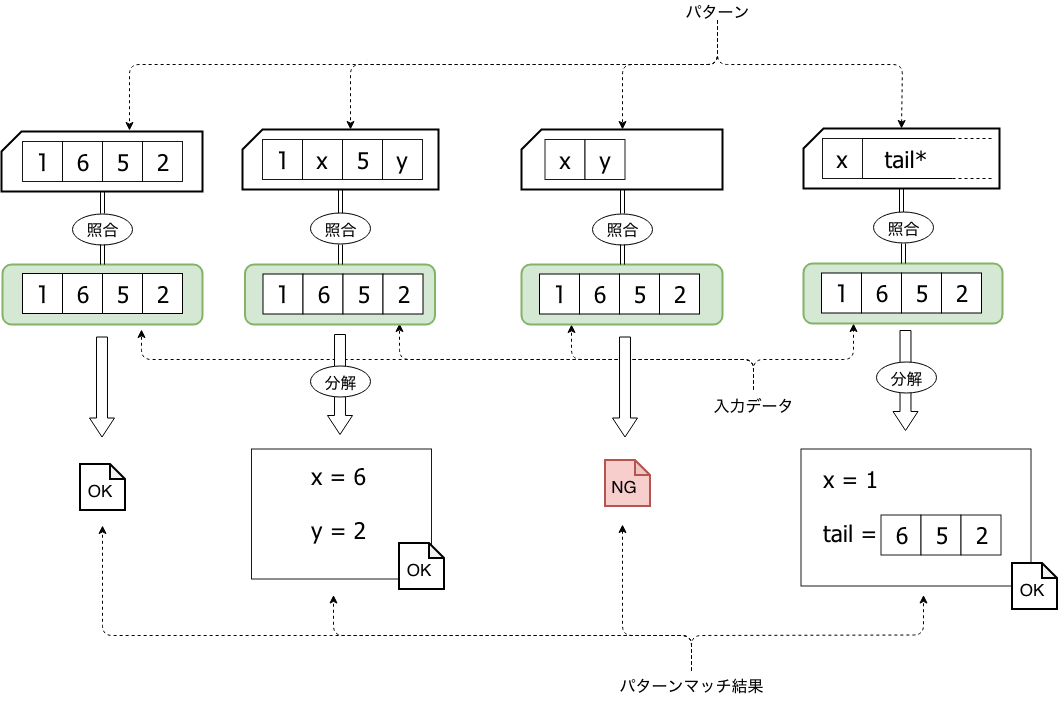
パターンマッチは以下の図のように、入力データを「パターン」と呼ばれる特定の構造と照合して、データとパターンが適合(マッチング)した場合に分解して要素を取り出します。

パターンマッチの凄いところは、入力データの値だけではなく、構造にも着目してデータを抽出できることです。上記の図は入力データとして同じ整数の配列([1,6,5,2])を用いて、4種類のパターンを用いてパターンマッチを実行している様子です。1番目のパターンは特に説明は不要だと思うので、二番目のパターンから説明するとパターン([1,x,5,y])のように、構造から値を抽出しておきたい場所を変数にしておけば、データ構造を分解することができます。抽出した変数は後の変換処理で利用できます。3番目のパターンはパターンマッチが失敗していますが、理由は簡単でパターンと入力データの長さが異なるからです。4番目のパターンは再帰処理でよく使うパターンで配列の先頭とそれ以外にデータを分割できます。

このようにパターンマッチを用いると、データ構造をパターンを用いて分解して処理ができるので、様々なアルゴリズムが書きやすくなるというメリットがあります。

パターンマッチの構文はプログラミング言語ごとに異なりますが、概ね「入力」と「パターン」と「変換処理」を記述できます。以下はscalaを用いた一番シンプルなパターンマッチ構文の例です。

入力 match {
  case パターン => 変換処理
}

変換処理では分解によって取り出した変数を利用した処理を書くことができます。そして、変換処理の結果自体がパターンマッチ全体の結果となります。パターンマッチに失敗した場合は一般的には例外が発生します。

最初の図の4つのパターンマッチをScalaで記述した例が以下になります。Scalaを知らなくても上記の図が理解できていれば、どんな処理をしているのか想像がつくと思います。

val result1 = Seq(1, 6, 5, 2) match {
  case Seq(1, 6, 5, 2) => "ok"
}
// result1 = "ok"

val result2 = Seq(1, 6, 5, 2) match {
  case Seq(1, x, 5, y) => x + y
}
// result2 = 8

val result3 = Seq(1, 6, 5, 2) match {
  case Seq(x, y) => x + y
}
// 例外発生！

val result4 = Seq(1, 6, 5, 2) match {
  case Seq(x, tail @ _*) => tail
}
// result4 = Seq(6, 5, 2)

パターンマッチとパターン

パターンはいくつかの基本形に分類されますが、以下は自分が特に重要だと思う9つの基本形です³。パターンマッチで一番誤解を受けいているのがこの部分で、この基本形を十分に理解せずにはパターンマッチを使いこなしているとは言えないと思います。そしてこの基本形を使いこなせるようになればパターンマッチ、ひいてはプログラミングの世界が大きく広がると思います⁴。

　
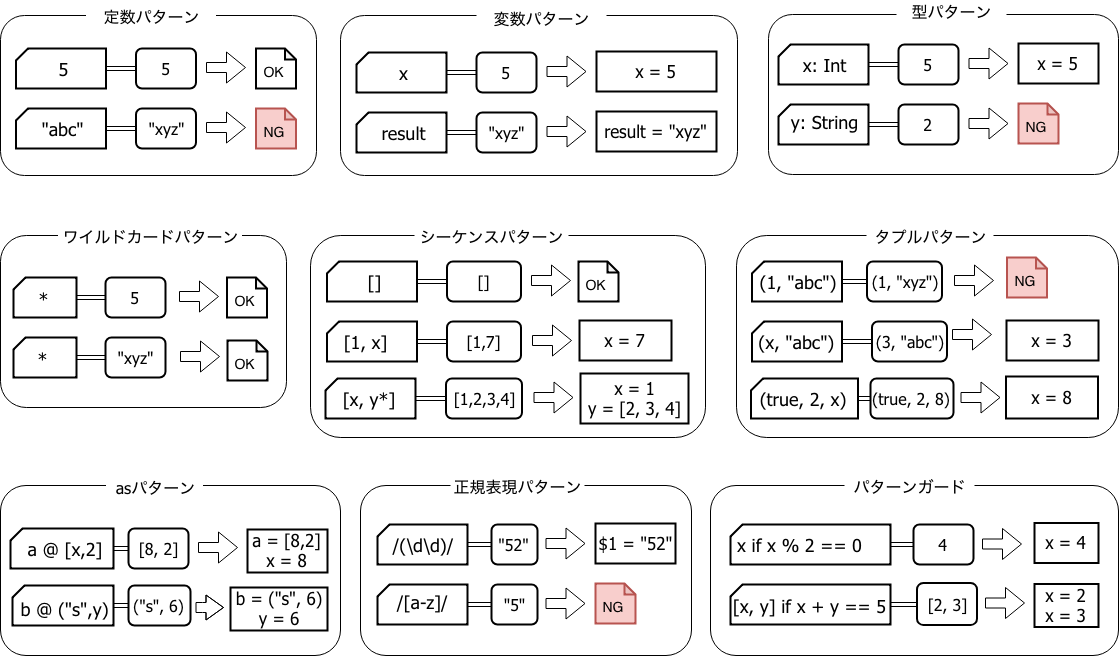
基本形は組み合わせてより複雑なパターンを記述することができます。重要な役割を果たすのが入れ子構造にすることが可能なシーケンスパターンとタプルパターンです。

　
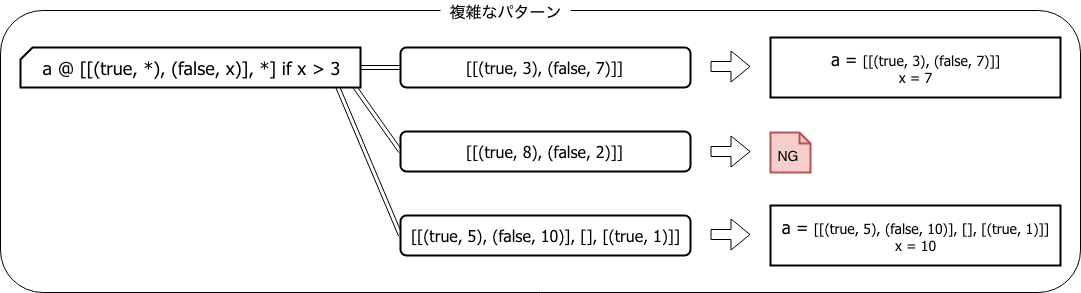
上記の複雑なパターンは「定数パターン」、「変数パターン」、「ワイルドカードパターン」、「シーケーンスパターン」、「タプルパターン」、「asパターン」、「パターンガード」の7つの基本形を組み合わせたパターンになります。このようにパターンは入れ子にすることで飛躍的に表現力が増し、応用範囲が広がります。さらにはパターンマッチで分解した結果を「変換処理」の中でさらにパターンマッチすることもできます。つまりパターンだけでなくパターンマッチ自体も入れ子にすることができます。以下の例はScalaを用いたパターンマッチを入れ子にした例です⁵。

val result = Seq(Seq((true, 5), (false, 10)), Seq(), Seq((true, 1))) match {
  case  a @Seq(Seq((true, _),(false, x)), _*) if x > 3 =>
    a match {
      case Seq(_, y @ _*) => x + y.size
    }
}
// result = 12

ここまで読んでいただいた方はパターンマッチにおける基本形の重要さが理解できたと思います。そして一番最初に図解したパターンがどの基本形にあたるかも簡単に分かると思います。プログラミングの重要な目的の一つはデータを処理することだと思います。そしてパターンマッチはデータ構造をパターンで分析し処理するのにうってつけの機能です。従ってパターンマッチは間違いなくプログラミングの本質に迫る機能だと考えられます。

パターンマッチの構造

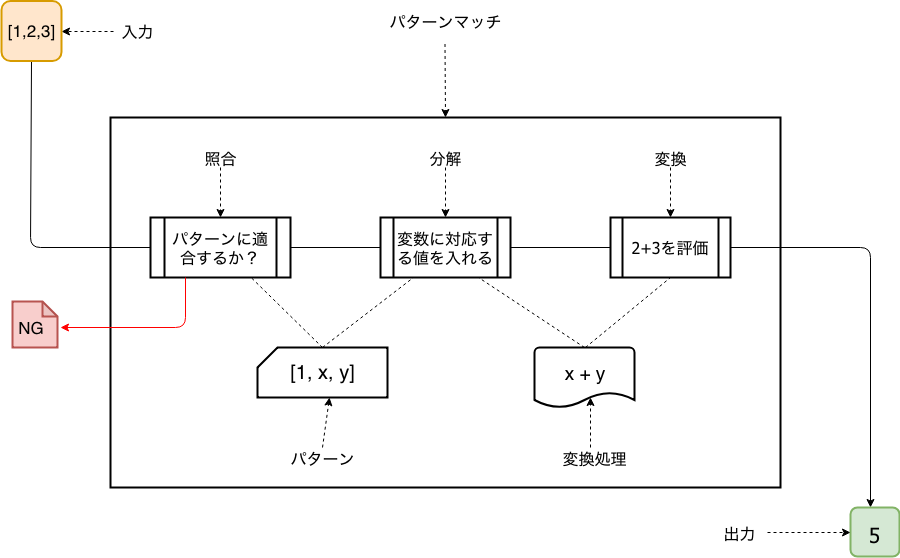
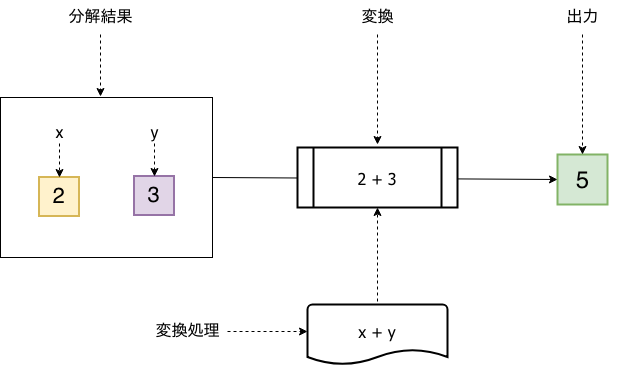
プログラミング言語のパターンマッチは、以下の図のとおり入力と出力がある一種の関数と考えることができます。パターンマッチの内部は「パターン」と「変換処理」と呼ばれるユーザが定義するデータと「照合(check)」、「分解(destructure)」、「変換(transform)」と呼ばれる３つの工程から構成されています⁶。

　
上記の図は「シーケンスパターン」を用いて、整数の配列[1,2,3]の入力に対するパターンマッチを実行している様子を示しています。この入力のパターンマッチは成功して実行結果として5を返しますが、もし、仮に入力が[1,2]だった場合にはパターンの照合に失敗して赤矢印で示した「NG」へ行き、パターンマッチが失敗します。

パターンマッチを関数とみたときにこのように失敗する可能性がある場合は、失敗しない関数（数学的な意味での関数、全関数とも言う）と区別して「部分関数」と呼ぶことがあります。部分関数を全関数にするにはパターンを網羅的にする必要があります。

パターンマッチと照合

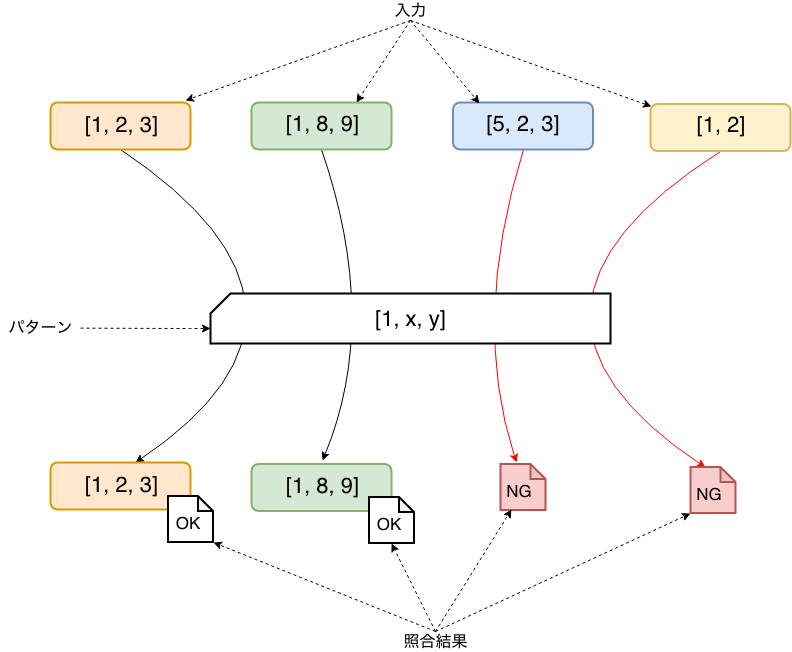
「照合」の役割は、以下の図のようパターンに適合(マッチ)する入力データを選別することです。そして適合したデータは次の「分解」のフェーズに送られます。

パターンマッチと分解

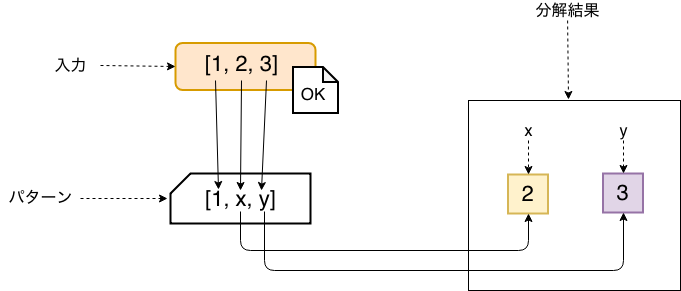
「分解」の役割は、以下の図のようにパターンに従ってデータを分解して、変数に対応する値を入力データから見つけて変数に入れることです。分解の結果は次の「変換」のフェーズに送られます。

この分解はパターンマッチ構文以外でも見ることができます。例えば以下は擬似コードですが代入がシーケンスパターンのパターンマッチになっています。

[a, *, b] = [1, 2, 3]
// a = 1, b = 3

このように代入に見えてパターンマッチになっているケースもあるので、実は知らないうちにパターンマッチのお世話になっているかもしれません。

パターンマッチと変換

「変換」の役割は、以下の図のように変換処理の変数に分解結果の変数を引き当てて、評価することです。評価した結果は出力としてパターンマッチ全体の結果になります。

パターンマッチと合成

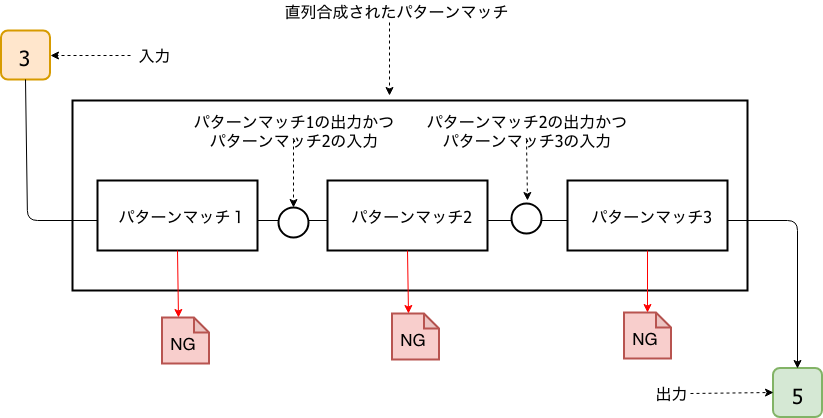
パターンマッチの合成には直列合成と並列合成があります。直列合成のイメージは以下の図のように通常の関数の合成のイメージと同じで前の関数の出力と後ろの関数の入力の型が合えば合成することができます⁷。

　
ソースコードの方が理解しやすい方がいるかも知れないので以下にScalaで２つのパターンマッチを直列合成をした例を記載します。

val match1 = (a:Int) => a match {case x if x % 3 == 0 => x * 2}
val match2 = (a:Int) => a match {case x if x > 5 => x * 10}
val composed = match1 andThen match2
composed(3) // 60
composed(5) // MatchError

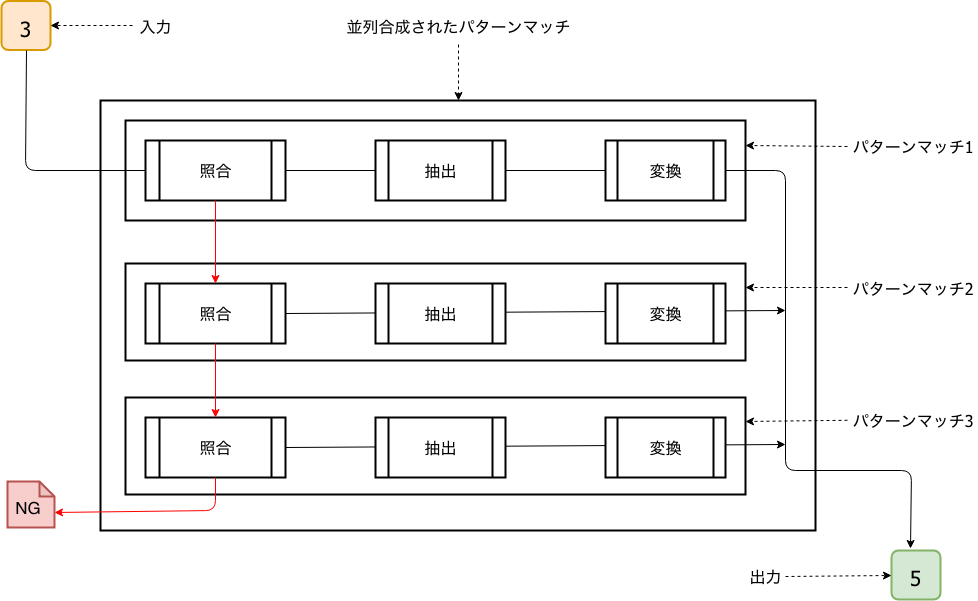
以下はパターンマッチの並列合成です。並列合成は大抵の言語のパターンマッチ構文に組み込まれているので、あまり「合成」と意識することは少ないかもしれません。しかし直列合成と比較するとプログラミングの論理演算であるandとorと類似していることが分かると思います。つまり、直列合成の場合はパターンマッチが全て成功しないと合成されたパターンマッチが成功しないのに対して、並列合成ではパターンマッチが一つでも成功すれば、合成されたパターンマッチが成功します。

　
以下は直列合成の例を並列合成に書き換えたものです。結果が変わっているのがわかると思います。

val composed = (a:Int) => a match {
                            case x if x % 3 == 0 => x * 2
                            case x if x > 1 => x * 10
                          }
composed(3) // 6
composed(5) // 50

パターンマッチとパターンの重なり

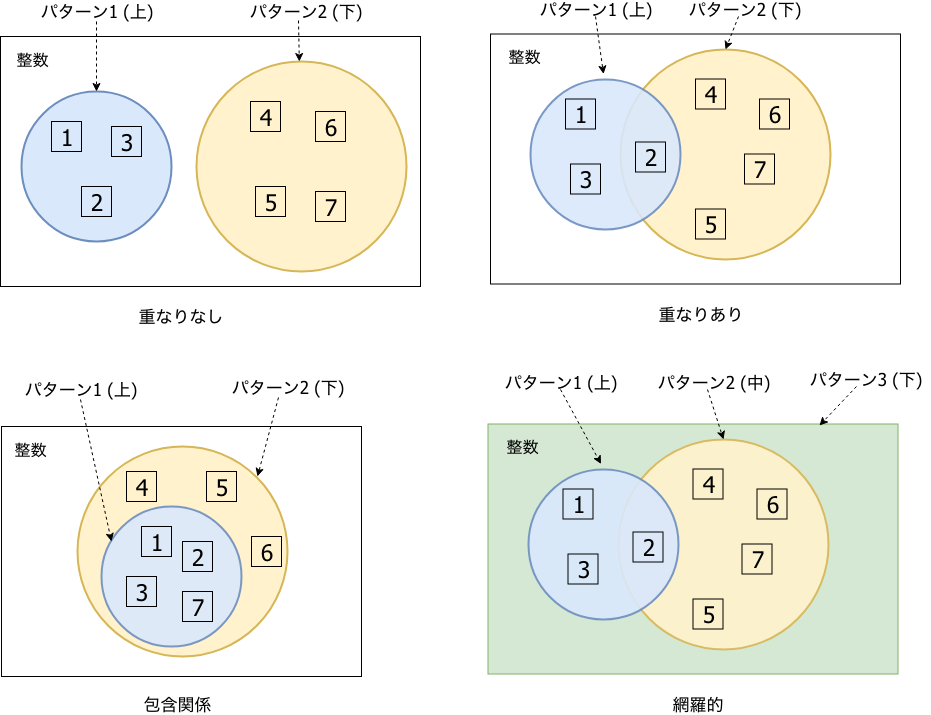
並列合成のパターンマッチの場合には、パターンの重なりを意識することが重要です。以下の図は整数の集合における基本的なパターンの重なりを分類したものですが⁸、このようにパターンを図で思い描けるようになるとパターンの設計に非常に役に立ちます。

　
並列合成では上のパターンマッチから順番に照合されるため、パターンに重なりがあると上のパターンマッチが優先されることになります。特に包含関係にあるパターンは上に大きいパターンを持ってくると下のパターンが隠れてしまって全く照合されない事態になるので、注意が必要です。

またパターンを網羅的にすることでパターンマッチの失敗がなくなり、無意識にバグを作り込むことを防ぐことができます。従ってパターンマッチは特に理由がない場合は網羅的にすることが望ましいです。網羅的にするのに適した基本パターンは「変数パターン」と「ワイルドカードパターン」になるので、並列合成の一番最後にこれらのパターンを入れることを検討してください。

パターンマッチと広がる世界

従来パターンマッチはHaskellに代表されるような関数型言語の十八番でしたが、現在では関数型プログラミングに源流を持たないプログラミング言語でもパターンマッチを実装するようになってきました。C#では7.0以降でパターンマッチが利用可能であり、Rubyでもすでにtrunkではパターンマッチが利用できます⁹。また比較的新しく出た言語は最初からパターンマッチが使える場合が多く、パターンマッチの世界は広がり続けています。仮にお気に入りの言語にパターンマッチがなかったとしても諦めるのはまだ早いかもしれません。使い勝手は言語に統合された機能よりは劣るかもしれませんが、パターンマッチのためのライブラリも数多く公開されています。

言語としての変わり種は Egisonです。「直感をそのまま表現するパターンマッチング 」という謳い文句で、パターンマッチとして非常に面白いので気になった方はぜひ触って見てください。

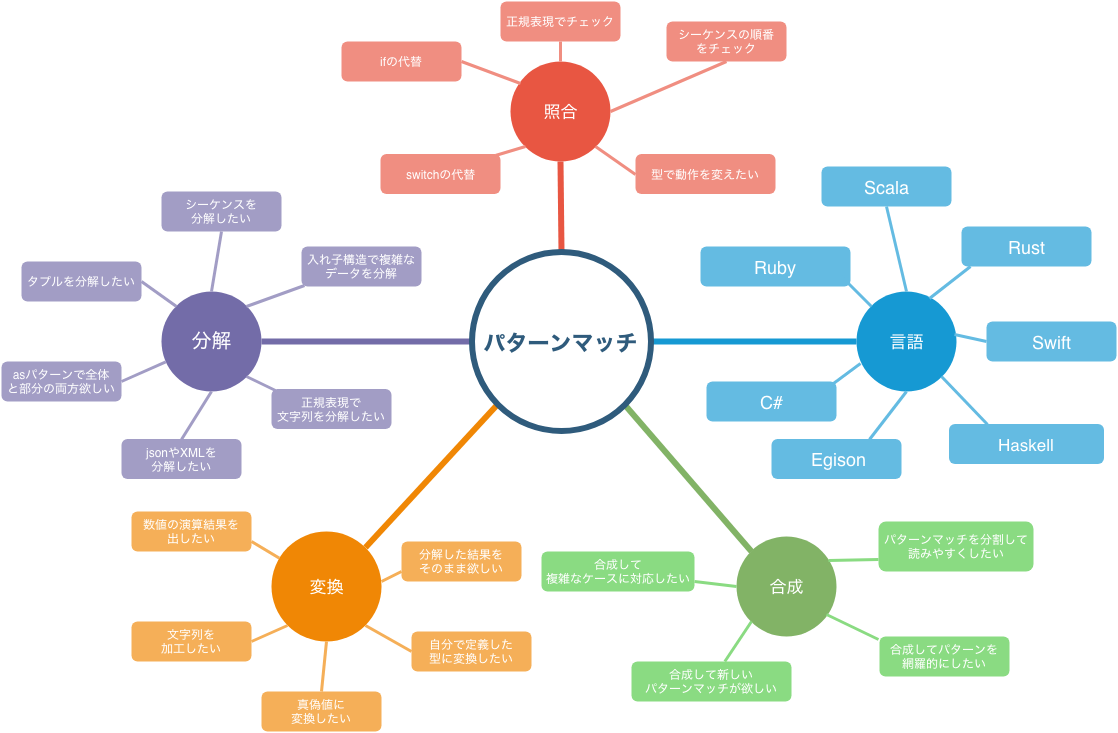
このように少しずつですが着実にパターンマッチが使える言語が増え続けているのは、パターンマッチがプログラミング全般で非常に用途が広く、使いこなすことで直接的にプログラマの能力を拡張するからだと思っています。以下の図は思いついたパターンマッチの用途です。

まとめ

以下、「パターンマッチ」のまとめです。

• 「パターンマッチ」は入力データを「パターン」と呼ばれる特定の構造と照合して、データとパターンが適合した場合に分解して要素を取り出す
• 「パターンマッチ」のパターンにはいくつかの重要な基本形があり、基本形を組み合わせてより複雑なパターンを表現できる
• 「パターンマッチ」は「照合」、「分解」、「変換」から構成される
• 「パターンマッチ」の合成方法は主に「直列合成」と「並列合成」の２種類があり、並列合成の方はパターンマッチの構文に組み込まれている場合が多い
• 「パターンマッチ」ではパターンの重なりを意識する必要がある
• 「パターンマッチ」は様々な言語で利用可能になってきている
• 「パターンマッチ」はデータを「パターン」として処理するためのプログラミングのツールであり、プログラマの能力を直接的に拡張する

パターンマッチは関数型プログラミングでは特に再帰関数と相性が良く欠かせない存在ですが、一般のプログラマへの浸透具合はいまいちと感じたので、関数型プログラミングの文脈からなるべく切り離して解説をしてみました。

本記事が「パターンマッチ」の理解と普及の一助になれば幸いです。

1. ここで言うぱ「パターンマッチ」はパターンマッチを実装しているプログラミング言語の総和でイメージしており、特定のプログラミン言語のパターンマッチを意味していません。従って、本記事で解説しているパターンマッチの機能や用語は個別の言語でそれぞれ異なる場合があります。 ↩

2. ここで言う「switch文」とはC言語のswitch文をイメージしています。また、ここではswitch文とパターンマッチとの歴史的な繋がりではなく、機能的な包含関係について「強化版」という表現をしています。 ↩

3. パターンの記述は疑似言語で記載しています。また、パターンマッチの対応を謳っているプログラミング言語でも、いくつかの基本形が使えない場合があります。しかし上の6つのパターンはだいたい使えるのではという感触です。 ↩

4. 9つの基本形は非常に重要なのでA４サイズで収まりがいいように図を工夫しました。チートシートとしてご利用ください。机や冷蔵庫に貼って忘れないようにするのもいいかもしれません(笑)。 ↩

5. ネストができることを示すだけの例なのでコードに特に深い意味はないです。 ↩

6. 工程の呼び方はいろいろあります。例えばdestructureとextractと呼んだりtransformをmapと呼ぶ場合もあるようですが、ここでは自分が一番分かりやすいと思った表現を採用しています。また、「照合」と「分解」だけを指して「パターンマッチ」と呼ぶ流儀も存在しますが、多くのプログラミン言語のパターンマッチの構文には変換処理も含まれるので、この記事では「変換」も含めて「パターンマッチ」と呼びます。 ↩

7. 実際には型だけでなく関数の定義域や値域を考慮する必要がありますが、数学的な話になってくるので詳細は割愛します。 ↩

8. 整数にしたのはイメージが簡単にできると思われるためであり、ここで説明するパターンの重なりは整数以外の集合にも同じことが言えます。 ↩

9. 正式にはRuby 2.7で利用可能になる予定です。 ↩