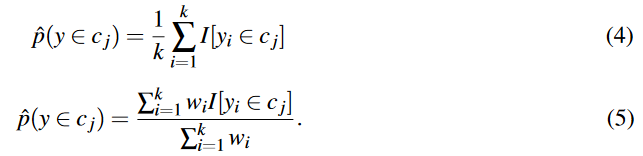Calibrated neighborhood aware confidence measure for deep metric learning 要約
読んだ論文
Calibrated neighborhood aware confidence measure for deep metric learning
Maryna Karpusha, Sunghee Yun, Istvan Fehervari
https://arxiv.org/abs/2006.04935v1
上記の論文を読んだので簡単にまとめます.Amazonの方のArxiv論文です.Metric Learningを読みたかったので,SoTA(https://paperswithcode.com/paper/calibrated-neighborhood-aware-confidence)漁っていたらたどり着いたのですが,Metric Learning手法に関する論文ではなく,その後処理に関する論文でした.
近年ではAI-SCHOLARさんが非常に流行しているので,私のQiita記事もいっそAI-SCHOLARさんに寄稿したほうが有意義かとも思いましたが,理解が一部甘いため,手軽に投稿できるQiitaに書いておきます.
3行でまとめる
- Metric Learningを分類問題に応用する際に,1つの比較対象と比べるより集団と比べた上でクラスを判定するほうが頑健性が高まる.
- kNNやWeighted kNNと比べ分類性能だけでなく,予測確信度が正確な手法NEDを提案する.
- 評価指標として予測確信度の正確さを図る指標も提案し,提案手法が優れていることを複数のデータセットを用いて示した.
1章:Background
1.1: Deep Distance Metric Learning (DDML)
Metric Learning (ML)の問題設定を改めて定式化している.記号だけおさらいしておく.
- $N$: データ数
- $ \bigl\{(x_i, y_i)\bigr\}_{i=1}^N $ : N件の入力+出力(カテゴリ)のペア
- $x_i \in \boldsymbol{R}^n, y \in C | C = \bigl\{c_1, ..., c_M\bigr\}$: 入力はn次元整数,yはCの要素でカテゴリ数はM
- $f: \boldsymbol{R^n} -> \boldsymbol{R^m}$ : n次元の入力をm次元の潜在空間に飛ばす写像関数f
- ただしこの関数をDDMLで訓練する.すなわち,同一クラスの$z_i=z_j$の距離は近くなり,異なるクラスの$z_k \neq z_l$の距離は遠くする.
- つまり(1)式 $d(z_i,z_j) << d(z_k, z_l)$
残る段落は関連研究のLossの紹介.
1.2: Confidence in Deep Learning
深層学習の出力は過学習しがちなので,予測結果には確信度を添えて出力したい.関連研究ではhold-outした検証データで予測確信度をキャリブレーションする方法1や,ベイズ推定による手法,Support setを用いる手法が紹介されている.恐らく本稿の提案手法NEDはSupport setを用いる手法に分類される.
2章: 提案手法NED
証明は付録にあるらしいのですがさておき,本題のNEDの核心は下記の式で後処理を行うことで予測確信度を算出する点です.
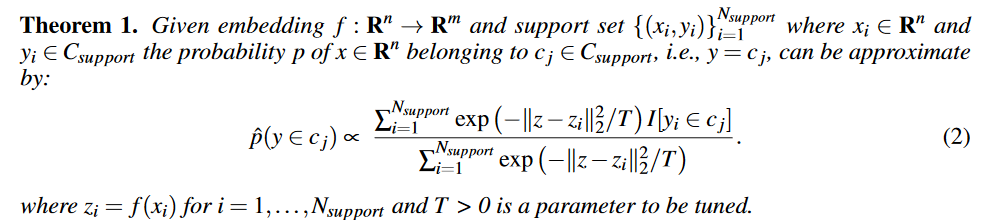
今回求めたい値(左辺)は$y$が$C_j$に属する確率$\hat{p}$です.個人的にはこの式を理解する前に,本稿で比較対象としているkNN(k-Nearest-Neighbor)とWeighted kNNの式をさらっておくと比較しやすくて良いと思うので,少し飛んで2.1節よりkNNの(4)式,Weighted kNNの(5)式を引用します.
ここで,実はI[]が何かと言うのは正直良くわからなかったのですが,直前に
The kNN classifier is a simple non-parametric classifier that predicts the label of an input based on a majority vote from labels of the kneighbors in the embedding space. Intuitively, the confidence score for every class can be selected as the percentage of nearest neighbors labels belonging to $c_j$ class:
と書いてあるため,$I[y_i \in c_j]$で,$y_i$がクラス$c_j$と一致するときに1,そうでないときに0を返す関数なのかなと考えました.とすると近傍k個のうち同一カテゴリ$c_j$に属する個数で確率を示すことができます.同様に(5)式は近傍の近さの順位に応じて$\boldsymbol{w}$で重み付けを行っているだけですね.
ここで,NEDの提案手法である(3)式に戻りましょう.なお,(3)式は上述した(2)式を$N_{support}$を$k$個の近傍要素に置き換えただけです.
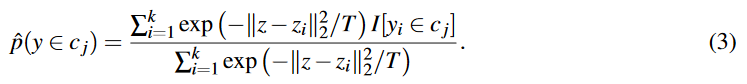
(5)式と比べていただきたいのですが,重み$\boldsymbol{w}$がsoftmaxライクな式に置き換わっているだけですね.すなわち,人の知見で決定していた$\boldsymbol{w}$をMetric Learningで得た潜在空間上の距離に基づいて決定しようとする手法がNEDです.expの中身は,今回の推定対象$z$と,近傍iの$z_i$(それぞれ潜在空間上の座標)から2乗ノルムを計算し,Tで除しているだけです.距離に応じた確率分布に変換しているイメージです.Tは温度パラメータでハイパラなので,距離が近いものを強めたいか,全体を緩やかに見たいかで設定すると良いです.感覚的に理解したい方はこの辺を参照(https://qiita.com/nkriskeeic/items/db3b4b5e835e63a7f243 ).
Algorithm1にはこれを実用する際に,全クラス($M_{support}$)に対して確信度を算出し,最大のものを予測カテゴリとするといった処理が記述されています.
3. 評価
ベースとなるDDMLモデルはOut of Scopeですが,今回はMetric LearningでSoTAの(多分)Soft Triplet Loss2を採用しています.Normalized and temprature-weighted version of cross-entropy lossとありますので,温度パラメータ付きの標準化SoftMaxかなと思います.
評価指標は,シンプルに分類時のAccuracyを使用するもの,Reliability Diagramsで可視化したもの,Expected Calibration Error (ECE)で数値的に評価したものの3点です.Reliability Diagramsは下図のように,横軸に確信度を並べbinで区切った時に含まれる各サンプルの正解率Accuracyを縦軸に描画する図です.斜めに入っている縦=横の赤点線と一致すれば,確信度推定が優れているとするわけです.
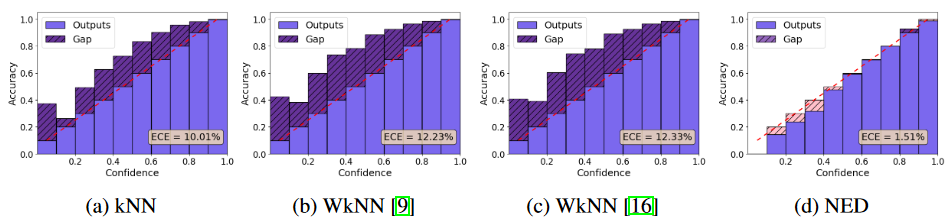
一方この可視化手法は各binのサンプル数を度外視しているため,定量評価するためにはサンプル数で重み付けしたError値に変換してあげる必要があります.この重み付けを行ったのがECEです.
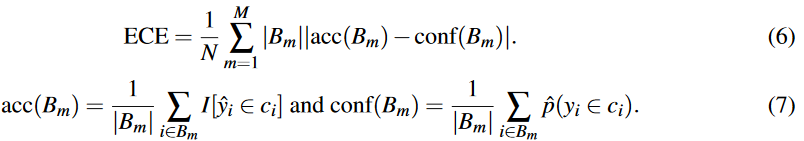
ここで,Nはサンプル数,Mはbin数,$B_m$はm番目のbinのindexセットです.実は(7)式の理解に戸惑ったのですが,これ中央の「and」は文字列なんですね...数式中にandとか書かないでほしかったです(もしくはカンマにして...).要するにandで2つの式に区切るという意味っぽいですね.すると,$acc(B_m)$は予測クラスが一致した数を$B_m$サイズで除しているので正解率,$conf(B_m)$は予測クラスが同一の確信度$\hat{p}$を$B_m$内で平均している感じですね.
最終的な評価結果は論文を参照してください.特にECEが優れていた点がNEDの貢献だと思われます.
所管
読み切るのは昼間の勉強会でじっししたんですが,なんだかんだQiitaでまとめ始めると1時間はかかってしまいますね.理解が甘かった点を読み直すを含めても.
本稿は手法自体はとてもシンプルな一つの数式で示される後処理手法で,Metric Learningで分類問題を解く場合には覚えておくと得するかなと思いました.実装も簡単そうですし.
-
C. Guo, G. Pleiss, Y. Sun, and K. Q. Weinberger. On calibration of modern neural netwroks. InProceedingsof the 34th International Conference on Machine Learning, 2017 ↩
-
Qi Qian, Lei Shang, Baigui Sun, Juhua Hu, Hao Li, Rong Jin. SoftTriple Loss: Deep Metric Learning Without Triplet Sampling, ArXiv, 2019 (ICCV2019 accepted), https://arxiv.org/abs/1909.05235 ↩